
Ovru-all
.pdf
6.5. Форми росту кристалів та їх стійкість
6.5.1. Форми вільного росту кристалів
Питання про рівноважні форми кристалів розглянуте у підрозділах 6.1.1 та 6.1.2. Рівноважна форма кристала кінцевого розміру – це фактично форма критичного зародка. Форми росту відрізняються від рівноважних. Кристали з опуклими округлими або гранними формами розростаються, залишаючись подібними до себе, лише за певних умов. Зокрема, в неперемішуваному матковому середовищі подібне розростання можливе, поки розмір кристала і відхилення від рівноваги не перевищують деяких значень [1,36]. Інакше кристали набувають так званої скелетної або дендритної (деревоподібної) форми. Ті та інші форми росту є на рис. 6.5. На рис. 6.15, показано ріст за нормальним механізмом кристалів гексагонолу та камфори за умови різних переохолоджень.
Рис. 6.15. Послідовні стадії втрати стійкості і розвитку дендритного зростка на кристалі циклогексанолу (a-d) [41] та форми росту кристалів камфори (e-h)[42, 43].
6.5.2. Стійкість кулястого кристала.
Дендрити виникають в наслідок нестійкості початкової опуклої форми кристала по відношенню до випадково виникаючих збурень.
Розглянемо, згідно з [1], стійкість кулі радіусом ρ, що росте з розчину. Розподіл концентрації розчину навколо кулястого кристала при
рівноважній концентрації на його поверхні Сρ=Се дається формулою (3.53). Якщо розв’язувати рівняння Лапласа спільно з умовою, що швидкість росту пропорційна пересиченню V=dρ /dt = β(Cρ − Ce )
181
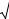
(β – кінетичний коефіцієнт) разом з умовою балансу маси на міжфа-
зній межі (3.54) – V=D |
(C∞ − Cρ ) |
|
, |
то можна знайти функції С(r), |
||||||||||||||
ρ(Ccr − Cρ ) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
V(ρ) i Cρ(ρ). Для випадку слабкого розчину ці функції наступні: |
|
|||||||||||||||||
С–С∞ = |
(C |
ρ |
− C |
∞ |
)ρ βC |
cr |
ρ |
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
r |
|
|
D |
|
|
1 + βCcrρ/D , |
|
(6.22) |
||||||||
|
|
|
|
|
|
|
|
|||||||||||
V=β(C∞ − Ce )/(1 + βCcrρ/D) |
|
і |
|
|
(Cρ − Ce ) |
|
= |
1 |
. |
|||||||||
|
|
|
(C∞ − Ce ) |
1 + βCcrρ /D |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Припустимо, що на поверхні кристала випадково виник виступ заввишки δ<<R , отже кривизна поверхні у вершини виступу збіль-
шилася на ~Мδ2/R, де число М тим більше, чим гостріше виступ. Вершина виступу потрапляє в пересичений розчин з концентрацією
Спов + (дС/дr)δ, де Спов=Cρ і дС/дr визначається з (6.22) при r=ρ. Підвищення концентрації на вершині виступу стимулює його подальше збільшення до макроскопічних розмірів і перетворює кулю на дендритний кристал, тобто веде до нестійкості. З іншого боку, рівноваж-
на концентрація С0 у вершини виступу з більшою кривизною також вище, ніж над рештою поверхні кристала, відповідно до формули
(6.2),
С0=Сe(1+ |
2Ωγ |
+ |
2Ωγ |
Mδ ), |
|
kTR2 |
|||
|
kTR |
|
||
де Се – рівноважна концентрація розчину над нескінченною плоскою поверхнею. Таким чином, поверхнева енергія, збільшуючи значення С0>Се, зменшує пересичення на вершині виступу (V = β(Cρ − C0 )), а
отже, протидіє його подальшому подовженню. Це означає, що поверхнева енергія сприяє збереженню форми поверхні.
Критерій стійкості має відобразити умови, в яких «кінематична сила», що подовжує виступ , поступається зменшенню термодинамічної (зменшенню пересичення). Іншими словами, швидкість вершини виступу щодо незбуреного фронту має бути від’ємною:
∆V=β((∂C /∂r)δ − C |
|
2Ωγ |
Mδ )<0. |
(6.23) |
|
e kTR2 |
|||||
|
|
|
|||
Підставляючи в (6.23) похідну дС/дr, знайдену з (6.22) і розв’язуючи рівняння, що виходить, відносно R, маємо критерій стійкості у вигляді
R<Rc 0.5Mr*(1+ |
1 + 4D/(Mβr*) |
), |
(6.24) |
182
де r* – радіус критичного зародка. Строгий аналіз, виконаний Маллінзом і Секеркою [44], використовує збурення у вигляді різних гармонік сферичних функцій, накладених на початкову сферичну фор-
му: r(θ,ϕ) = ρ + δYlm (θ,ϕ) , де ρ – початковий радіус сфери, Ylm – сферична функція, яка є розв'язком рівняння Лапласа. Локальна кри-
визна поверхні для такої форми залежить від θ і ϕ:
|
1 |
|
1 |
|
|
2 |
|
δY |
δΛY |
|
|
k = |
|
+ |
|
|
; |
k(θ,ϕ) = |
|
(1 − |
ρ2lm ) − |
ρ2 lm . |
(6.24) |
R |
R |
2 |
ρ |
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
Відповідно, згідно з формулою (6.2) біля виступів більше рівноважна концентрація:
cnl (θ,ϕ) = c0 (1 + |
2σΩ |
+ (l + 2)(l − 1) |
σΩδY |
|
|
RTρ2lm ) . |
(6.25) |
||
ρRT |
Відтік речовини у середовищі від цих ділянок є фактором, стабілізуючим форму поверхні. Якщо
ρ< ρкр |
(l) = ( |
(l + 1)(l + 2) |
+ 1)R* , |
(6.26) |
|
||||
|
2 |
|
|
|
форма абсолютно стійка – мале збурення відповідної форми з часом зникає. У якості відносного критерію втрати стійкості береться умова, що відношення
& |
|
ρcr (l))/(1 − |
R |
* |
|
|
|
δ /δ |
= (l − 1)(1 − |
|
) |
(6.27) |
|||
ρ/ρ |
ρ |
||||||
|
ρ |
|
|
||||
& |
|
|
|
|
|
|
|
перевищує одиницю. Тоді збурення форми розвиваються швидко. Згідно з [44], при великих швидкостях поверхневих процесів
(βρ*/D>> 1 або βTρ*/αT>>1 для випадку росту з розплаву) куля стійка, тільки якщо її радіус не перевершує МRС, що при l = 2 складає 7RС. Навіть при невеликих переохолодженнях, що виключають спонтанне зародження в розплаві, але що забезпечують помітну швидкість росту, ρ* є величина порядку 10–6 ÷10–4 см, тобто Rс ≈ 10–6
÷10–3 см. Наприклад, для заліза (¬ = 1.2-10–23 см3, γ = 0.204 Дж/м2) при переохолодженні ∆Т = 10° кулястий кристал стійкий лише до розміру ~ 2.5•10 –6 см. Зі збільшенням переохолодження критичний радіус стійкості зменшується ~1/∆T.
Згідно з [1], значення Rc, розраховані за формулою (6.24), близькі до значень передбачених теорію малих збурень [44], якщо покласти 2М = 2 + (l + 1) (l + 2), де l — номер гармоніки збурення. Значення l = 2 відповідає перетворенню кулі на еліпсоїд, l = 3 відповідає симетрії тетраедра, l = 4 – куба і т. д. Що вище симетрія збурення, тобто
183
що більше l, тим більш стійка куля по відношенню до такого збурення. Фізичною причиною, що зумовлює появу і розвиток збурень тієї чи іншої симетрії, є анізотропія кінетики росту кристала. Симетрія кутової залежності кінетичного коефіцієнта злегка відрізняється від сферичної навіть для шорстких в атомному масштабі поверхонь.
Як видно з рис. 6.15, на початковій стадії втрати стабільності форми росту виступи, пов’язані з анізотропією швидкості росту, починають випереджати інші ділянки міжфазної межі. Подальше їхнє просунення у пересичений розчин призводить до утворення дендритів. Кожен стовбур розвиненого дендриту росте вже незалежно від первинних виступів і має форму, близьку до параболоїда, причому швидкість його росту визначається кривизною на вершині параболоїда. На певній відстані від вершини радіус кривизни поверхні параболоїда перевищує критичний Rс , і ця поверхня також втрачає стійкість – виникають бічні гілки дендриту.
При різкому збільшенні переохолодження кількість виступів перевищує число, пов’язане з анізотропією швидкості росту
(рис. 6.15, j).
6.5.3. Стійкість форми багатогранника
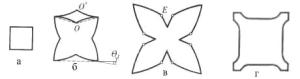
Досвід показує, що досконалі гранні форми кристалів мають місце тільки за дуже малих пересичень. На рис. 6.16 показано схеми перетворення досконалого кристала у скелет [1]. На першому етапі перетворення з’являються прогини граней з максимальними кутами при їх центрах. Потім в центрах граней утворюються западини, де скупчуються домішки, і ознаки суцільної грані втрачаються.
Рис. 6.16. Послідовні стадії (а-в) розвитку скелетного кристала.
Скелетне зростання обумовлене непостійністю пересичення уздовж граней. Розподіл пересичення над гранню можна знайти, розв’язавши рівняння дифузії або теплопровідності з крайовими умовами, що виражають постійність потоку речовини або теплоти до кожної точки грані. Відповідний розв’язок підтверджено експериментально для двовимірного випадку за формою інтерференційних ліній під час росту кристала із сольового розчину (див. в [1]) і за формою області закристалізованих рідких кристалів холестерилкапрона-
184

ту навколо кристалу антрацену, зростаючого з бінарного органічного розплаву антрацен– холестериловий ефір капронової кислоти [45].
Чернов [1] розглянув випадок зростання багатогранника з розчину в наближенні сферично симетричної апроксимації дифузійного поля навколо нього. При такому дифузійному полі кожна грань перетинається декількома лініями рівних концентрацій (або ізотермами
– при зростанні з розплаву), причому біля вершин проходять лінії, що відповідають великим пересиченням або переохолодженням.
Оскільки згідно з (6.22) на поверхні кристала дс/дr ~β/D, різниця пересичень в центрі грані і у вершини ~βL/D. Тому, якщо розмір крис-
тала настільки малий, що βL/D <<1 (суто кінетичний режим), пересичення на поверхні практично постійне і дорівнює пересиченню в об'ємі маткового розчину. Те саме має відбуватись при ідеальному перемішуванні розчину для кристалів будь-яких розмірів. В цьому випадку грані кристала практично плоскі (рис. 6.16, а). Зі збільшенням розміру кристала пересичення над центральними ділянками граней стає менше, ніж над вершинами і ребрами. Проте, як показує досвід, поверхня залишається макроскопічно плоскою. Отже, має існувати механізм, що компенсує непостійність пересичення.
Причиною, що підтримує поліедричну форму зростаючого кристала, є анізотропія швидкості росту V (n), n – вектор нормалі . Дією поверхневої енергії в [1] нехтується, що виправдано досить великими (~10–2 см) розмірами стійких многогранників. Мірою анізотропії швидкості зростання прийнято параметр θ =d(lnβ)/dp, р характеризує орієнтацію (нахил) поверхні. Якщо грань приймає прогнуту форму, то густина сходинок, отже, і кінетичний коефіцієнт для центральних, найбільш викривлених її ділянок виявляється більше, ніж для ділянок біля вершин та ребер (див. рис. 6.16, б). При сильній залежності V(р), тобто при θ>1, достатньо відхилення порядку 1 градуса від орієнтації сингулярної грані, щоб зберегти швидкість V, постійною для будь-якої точки викривленої грані:
V(р, С–С0) = β(р(х)) (С(х) - С0) = Сonst, |
(6.28) |
де кінетичний коефіцієнт β(р) = β(р=0) 
 1 + p2 ). Непостійність пере-
1 + p2 ). Непостійність пере-
сичення С(х)–С0 уздовж грані (див. рис. 6.16, г) компенсується непостійністю локальної орієнтації (щільність сходинок), а отже, і кінетичного коефіцієнта – β=β(р (х)). Величина добутку β(р1) (С1 — С0)
185
фізично визначається активністю центру, що генерує шари зростання на грані.
Якщо пересичення більше критичного, необхідного для виникнення плоских зародків на даній грані в околі вершин, то джерелами шарів зростання будуть саме останні. При пересиченнях, близьких до критичного, провідними джерелами утворення нових шарів можуть виявитися також дислокації, що виникли в процесі зростання і виходять на поверхню в околицях вершин, де пересичення найбільше. Вважаючи відносні зміни пересичення уздовж грані, а також зміни локальних нахилів малими і розкладаючи (6.28) по цих змінах, легко отримати різницю нахилів в центрі грані р2 і коло вершини р1 (за умови постійної швидкості):
р2-р1 = |
(С1 - С2 ) |
. |
(6.29) |
|
|||
|
(С1 - С0 )q |
|
|
Якщо відносна зміна пересичення (С1 — С2) / (С1 — С0) @ 0.2, а
q ~10, то р2-р1 » 2×10–2 , тобто для компенсації непостійності пересичення достатньо зміни локальних нахилів ~ 1°, що згадувалося вище.
Що більше розмір кристала в порівнянні з D/b, тим більше мають викривлюватися його грані, аби компенсувати неоднорідність пересичення. Поява прогинання в центрі грані у разі великих пересичень веде до подальшого погіршення живлення цієї ділянки і, отже, до ще більшого його відставання від вершин. Викривлення призводить до появи на поверхні ділянок з великими значеннями кінетичного коефіцієнта, а при цьому падає його анізотропія (при великих нахилах збільшення числа сходинок вже мало сприяє збільшенню швидкості росту). В результаті цих змін викривлення збільшується ще більше і так далі. Таким чином, досягнення деяких критичних значень локальних нахилів веде до лавиноподібної втрати стійкості, а точніше, – до неможливості розростання многогранника подібно до себе (рис. 6.15, в).
Викривлені форми росту кристалів срібла й вісмуту показано на рис. 6.17. Перші дві фотографії показують кристали на фоні бінарних розплавів. А на рис. 6.17, в показано декантований кристал (після скидання розплаву). Кінетичний коефіцієнт різко збільшується із збільшенням локального нахилу поверхні, тобто щільності сходинок, в кожній точці, доки щільність сходинок мала. При великих нахилах перекриття дифузійних полів сходинок достатнє сильне, і кінетичний коефіцієнт грані практично не залежить від її орієнтації. Ця область відповідає лінійній залежності V(р). Згідно з морфологічними і кіне-
186

тичними даними [1] область сильної залежності V (р) простягається до значень локальних нахилів р ~ 10–2 ÷ 10–1 . Тому в якості критичного значення максимального нахилу поверхні в центрі грані ркр, при якому починається скелетне зростання, можна брати згадані вище значення. Розрахунок показує, що нахил ркр досягається в центрі грані, коли розмір кристала становить
Lкр=f(θ)(ркp–р1)D/β(р1). (6.30)
Це і є максимальний розмір кристала, перевищення якого веде до скелетного зростання. Для росту з розплаву аналогічний критерій має вигляд
Lкр=f (θ)(ркp–р1)αT/βT(р1), (6.31)
де αT – коефіцієнт температуропроводності, βT – кінетичний коефіцієнт для росту з власного розплаву, а функція f (θ) ≈ 2.5, якщо θ>1, і f (θ) ≈ 1, якщо θ≤1.
Рис. 6.17. Викривлення форми росту гранних кристалів [46],
а– срібла; б, в – вісмуту; в – декантований кристал.
6.5.4.Чисельні розрахунки еволюції форми кристалів
Наведені нижче аналітичні теорії стійкості форм росту кристалів мають певні обмеження – при розгляді округлих форм застосовувався метод малих збурень, а при аналізі стійкості гранних форм розглядалася лінійна залежність від пересичення швидкості росту на ділянках біля вершин кристалів, де утворюються нові шари росту. Ріст вершин досить малих кристаликів зумовлений утворенням нових двовимірних зародків, і в цьому випадку має місце експоненціальна залежність швидкості росту від локального пересичення.
Одним із авторів посібника вільний ріст кристалів моделювався на основі чисельних розв’язків рівнянь дифузії або теплопровідності з урахуванням умов балансу тепла або речовини на міжфазній межі й кінетики поверхневих процесів приєднання атомів відповідно до розглядуваного механізму росту [47-51]. На рис. 6.18, а показана сітка вузлів, що використовувалася при розгляді двовимірних задач віль-
187
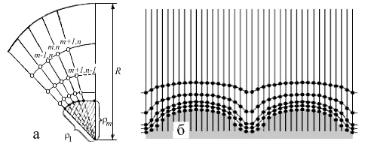
ного росту кристалів [50], на рис. 6.18, б – для задач спрямованого твердіння [52].
Рис. 6.18. Сітки, що перебудовуються,
для розгляду двовимірних задач росту кристалів:
а – вільного росту [50], б – спрямованого затвердіння [52].
Застосування однорідних різницевих схем зі згладжуванням, наприклад, розмазуванням теплоти кристалізації, як добавки до теплоємності найближчих комірок сітки (метод фазового поля), є виправданим у багатьох випадках. Проте, при розв’язку задач росту кристалів з рухомими поверхнями, що змінюються за формою, коли локальна кривизна поверхні істотно позначається на швидкості росту, раціональним є явне виділення поверхні розділу фаз з розрахунком змін координат поверхневих точок і кривизни межі.
При розгляді двовимірних дифузійних задач в кінцевих різницях розв’язувалося рівняння дифузії, записане в циліндричних координатах
(дC/дt)=D [(д 2C/дr 2)+(1/r)(дC/дr)+(1/r 2)(д 2C/дθ2)]. |
(6.32) |
Відповідні похідні виражалися через значення концентрацій у вузлах криволінійної сітки (рис. 6.18, а). Сітка вузлів, в яких розраховувалися концентрації, будувалася наступним чином. З центру кристала до самих країв кювети проводилися радіальні промені через рівні інтервали за кутом. З міркувань симетрії розглядався сектор, що відповідає анізотропії швидкості росту, наприклад, 45° для зростання квадратного кристала (рис. 6.18, а). Інтервали за відстанню уздовж радіальних променів від поверхні кристала до краю кювети вибиралися не постійними, а такими, що зростають у арифметичній прогресії, згідно (3.46). Похідні за координатою r записувались так само, як і в
підрозділі 3.4.3. А похідні за кутом θ знаходили після визначення інтерполяцією концентрацій на найближчих радіальних променях у
188
точках з координатою r, що дорівнювала координаті r розглядуваного вузла.
Методом прогону на послідовних часових інтервалах розраховувалися концентрації у всіх вузлах сітки, що задаються індексами m, n (за кутом і за відстанню уздовж радіального променя), а також координати поверхневих вузлів і значення поверхневих концентрацій. Локальні швидкості росту знаходили згідно з певними функціями (теоретично доведеними, або апроксимуючими експериментальні дані) їхньої залежності від величини поверхневого пересичення V(σп) (σп=(Cп–Cе)Се), а нові значення поверхневих концентрацій знаходили з умови балансу мас на міжфазній межі, записаної для даної точки поверхні кристала, після визначення концентраційного поля (за винятком поверхневих концентрацій). У зв'язку зі зміною координат поверхневих вузлів після кожного циклу – « прогону» сітка перебудовувалася: відповідним чином змінювалися координати всіх вузлів і перераховувалися концентрації для нового положення вузлів через визначувані значення градієнтів концентрацій.
У разі розгляду росту за нормальним механізмом задавалася анізотропія поверхневого натягу і кінетичного коефіцієнта. Для кубічного кристала кутова залежність вільної поверхневої енергії та кінетичного коефіцієнта:
γ=γ0(1+zγ cos4θ), |
(6.33) |
βs=β0(1+zβ cos4θ), |
(6.34) |
де zγ та zβ – коефіцієнти, що задають ступінь анізотропії. Поверхнева енергія враховувалась через поправку Гіббса-Томсона до пересичення – σп r*/r, відповідно, швидкість росту шукалася з формули
Vn=βsσп (1–r*/r), |
(6.35) |
де βs – анізотропний кінетичний коефіцієнт; r* – радіус критичного зародка; r – локальний радіус кривини поверхні. А у випадку анізотропної поверхневої енергії швидкість росту знаходили, враховуючи формулу Херінга (6.2):
|
Ω |
γ + |
∂ 2 γ |
|
|||
|
|
|
|
|
|
(6.36) |
|
|
|
|
2 |
||||
Vn=βsσп (1 – Ks |
∂θ |
), |
|||||
|
kT |
|
|
|
|
||
де Кs – локальна кривизна поверхні, а вираз у великих дужках (6.36) дорівнює γ0(1–15zγ cos4θ). У напрямку максимуму поверхневої енер-
189
гії (θ = 0) швидкість росту максимальна, оскільки мінімальним є зсув Гіббса-Томсона до пересичення.
На рис. 6.19, а показано еволюцію форми кристала при заданій початковій округлій анізотропній формі. Якщо задається анізотропія
γ і βs, виступи розвиваються швидше у відповідних напрямках. Але вплив анізотропії поверхневого натягу залишається істотним, доки розміри кристалика не перевищать значення r* приблизно у 100 разів. Моделювання росту анізотропної частинки з розплаву за подібною методикою виконано в [50]. Відомі числові розв’язки задачі утворення дендритної форми на основі розгляду рівняння Лапласа, наприклад, [53].
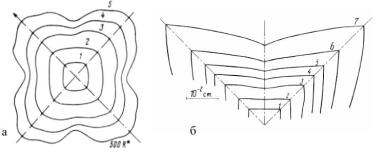
Рис. 6.19. Еволюція форми росту кристалів [50,51],
а – zγ=zβ =0, (С∞–Се)/Се=0.17, С∞=0.8, r1=r0(q)=300r*+19Cos4q, Г0=g0W/kT=2.24×10–8 cм, D=2.8×10–5 cм2/с, t5=0.004 c;
б – Bi + 20 ваг.% Sn, b=0.05 cм/c, g/kT=0.134, V=bss5/6exp(-K/ss), K=pg/3k2T2, t7=572 c.
У сучасних роботах [54, 55] для розв’язку задач формотворення кристалів використовують гратковий метод, заснований на кінетичному рівнянні Больцмана (у р. 3.4.3 згадувався варіант методу для опису течій у рідині). Використання дуже дрібних граток (сіток) дозволяє визначати досить точно положення міжфазної поверхні в рамках моделі фазового поля (див. підрозділ 3.4.2) й розраховувати локальний нахил поверхні та її кривину, що необхідно для урахування анізотропії поверхневої енергії та кінетичного коефіцієнта. Зрозуміло, що таке моделювання потребує застосування сучасних потужних ЕОМ, об’єднаних у так звані кластери. Головною проблемою методик, основаних на кінетичному рівнянні Больцмана, є труднощі підбору коефіцієнтів, що характеризують акти розсіювання обраних елементів маси, таким чином, щоб результати моделювання відповідали відомим з експериментів значенням коефіцієнтів дифузії, теп-
190
