
Ovru-all
.pdf
відразу встановлюється концентрація В-компонента Со/2. Концентрація В-компонента в другому прутику змінюється з часом за формулою
|
|
C(x,t)=(Co/2)[1−erf(ω)], |
(3.8) |
|||||||
|
|
|
2 |
ω |
−α |
2 |
|
|
||
де ω=x/(2 Dt ); erf(ω)= |
|
|
||||||||
∫ e |
dα – |
так званий інтеграл похибок. |
||||||||
|
|
|||||||||
|
|
|
|
π 0 |
|
|
|
|
||
Формула (3.8) є розв’язком диференціального рівняння (3.6) за названих початкових та граничних умов.
Коефіцієнти дифузії.
Залежно від умов проведення дослідження розрізняють кілька коефіцієнтів дифузії. Найпростіша ситуація має місце при розгляді дифузії радіоактивного ізотопу, що міститься у дуже малих концентраціях, за умови, що кристал є однорідним у всіх інших відносинах. У цьому випадку єдиним фактором, що дає потік радіоактивних атомів, є градієнт їхньої концентрації. Коефіцієнт дифузії, виміряний у зазначених умовах, позначають D*, і звуть коефіцієнтом дифузії міче-
них атомів. Термін коефіцієнт самодифузії відноситься до випадку,
коли наявні радіоактивні атоми тієї самої речовини, що й неактивні. У випадку, коли в деякому напрямку діють рушійні сили, молекули в середньому мають більшу ймовірність перескоків у напрямку дії сили, скажімо х, ніж у протилежному. Таким чином, рушійна сила на-
дає атомам середню швидкість <V>f у напрямку х і зумовлює вклад С <V>F в потік атомів.
Якщо включити в розгляд рушійні сили (це може бути, наприклад, сила, що діє на іони в електричному полі), то основне дифузійне співвідношення набуде вигляду
j = - D*(dC/дх ) + C<V>f . |
(3.9) |
В деяких важливих випадках рушійна сила F і, відповідно, швидкість дрейфу <V>f пропорційна градієнтові концентрації (дС/дх ). Тоді можна об’єднати два члени в правій частині (3.9) і записати вираз
ji= – DI (dCi/дх ), |
(3.10) |
i
в якому
DiI = D*– Ci<V>f /(dCi/dx),
DiI - власний коефіцієнт дифузії компонента i.
81
Рушійні сили, пропорційні градієнтові концентрації, виникають у наступних випадках: 1) внаслідок появи дифузійного потенціалу в іонних кристалах за різної рухливості катіонів; 2) через виникнення дифузійного потенціалу при дифузії двовалентної домішки в одновалентних ґратках; 3) за наявності градієнтів концентрації в неідеальних твердих розчинах.
Коли атоми двох сортів перемішуються, швидкість перемішування залежить від дифузійних характеристик обох компонентів. Коефіцієнт "взаємної дифузії" можна визначити як параметр, що характеризує швидкість змішування. У випадку дифузії в ізольованій системі він визначає швидкість гомогенізації (зникнення первісного градієнта концентрації).
Якщо в експериментах зі взаємної дифузії обидва компоненти мають різні власні коефіцієнти дифузії DiI , то виникає результуючий
потік атомів через будь-яку площину в дифузійній зоні. Це викликає розбухання кристала з одного боку дифузійної площини й усадку – з іншого. Тобто кожна площина в дифузійній зоні набуває швидкість руху відносно реперної площини, фіксованої на краю зразка. Коефі-
цієнт взаємної дифузії |
~ |
|
i-го компонента |
D виражається через потік j’i |
|||
|
′ |
~ |
|
відносно реперної площини ji = –D (дCi/дх ). |
|
||
В двокомпонентних кристалах з постійною густиною атомів виконується співвідношення
СА + СВ = Const ; (дCА/дх )= -(дCВ/дх ); j’А=– j’В,
і тому в формулах для потоков j’А і j’В, фігурує один і той самий коефіцієнт взаємодифузії. Його можна виразити через парціальні коефіцієнти дифузії за формулою Даркена:
~ |
I |
I |
(3.11) |
D = DA хВ+ DB хА, |
|||
де хА = СА/(СА+ СВ); хВ = СВ/(СА+ СВ).
При розгляді задач кристалізації зазвичай доводиться мати справу
зкоефіцієнтом взаємної дифузії, який позначають просто D.
3.1.2.Внутрішнє тертя
Змакроскопічного погляду внутрішнє тертя визначається за законом Ньютона
Fz=h½duz/dx½dS, |
(3.12) |
де Fz – сила тертя між двома сусідніми шарами газу або рідини, які рухаються з різними швидкостями uz(х) уздовж осі z (рис.3.2). Ця
82
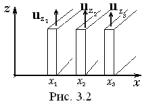
сила прямо пропорційна площі шарів dS, коефіцієнту в’язкості і градієнту швидкості вздовж осі x, перпендикулярної до потоку. Коефіцієнт в’язкості вимірюється в одиницях Па·с (Паскаль-секунда). Він дорівнює силі тертя, яка діє в напрямку дотичної на 1 м2 площі шару, якщо градієнт швидкості дорівнює 1 м/с.
Дія сили тертя на деякий шар з боку сусідніх призводить до зміни його імпульсу. При цьому імпульс сусідніх шарів теж змінюється. Цей процес можна розглядати як перенесення імпульсу в напрямку осі x. Помноживши обидві частини рівнян-
ня (3.12) на час dt, одержимо
Fzdt=h½duz/dx½dSdt
або
dK=-h(duz/dx)dSdt, (3.13)
де dК – кількість руху, що переноситься; знак “ мінус” поставлено тому, що напрям перенесення і напрям градієнта швидкості протилежні один одному.
Одержане рівняння з погляду математики повністю еквівалентне рівнянню дифузії (3.1).
3.1.3. Теплопровідність
Рівняння, яке дозволяє обчислити кількість теплоти, що переноситься в речовині через площинку площею dS за час dt в умовах практичної відсутності конвекції і тепловипромінювання, називають законом Фур’є. Аналітично він записується так:
dQ = -k(dT/dx)dSdt, |
(3.14) |
де dQ – кількість теплоти; k – коефіцієнт теплопровідності; dT/dx – градієнт температури в напрямку осі x. Знак “ мінус” означає, що тепло переноситься від більш нагрітих до менш нагрітих частин тіла. Математично рівняння Фур’є еквівалентне рівнянням дифузії і перенесення імпульсу.
Якщо розглядати баланс теплоти, що входить у деякий малий об’єм і виходить з нього згідно з тією самою схемою, що наведена на рис. 3.1, то прийдемо до другого рівняння Фур'є. Поділимо різницю того тепла, що входить, і того, що виходить, на теплоємність об’єму,
що розглядається, crdSdx (с – питома теплоємність у розрахунку на одиницю маси, r - густина; dSdx – об’єм). У такий спосіб знайдемо приріст температури за час dt. Відповідне співвідношення,
83
¶T |
|
¶ |
T |
¶T |
|
|
¶t |
= |
|
a |
|
, |
(3.15) |
|
|
|||||
|
¶x |
|
¶x |
|
||
є залежним від часу рівнянням теплопровідності. Величину aT=k/cr звуть коефіцієнтом температуропровідності. Він має таку саму розмірність, що й коефіцієнт дифузії (м2/с), і також є характеристикою речовини.
Рівняння (3.15) математично збігається з рівнянням (3.5). Отже, для теплопровідності рівняння, аналогічні рівнянням (3.6) і (3.7), також мають місце за відповідних умов. Якщо умови для дифузії або теплопровідності такі, що концентрація або температура залежать не від часу, а тільки від координат, то відповідне концентраційне чи температурне поле буде стаціонарним. Такі поля можна визначити,
розв’язуючи рівняння Лапласа Ñ2С=0 або Ñ2Т=0 за певних граничних умов.
Отже, усі явища перенесення з погляду математики підпорядковуються одній закономірності
I = -b(dG/dx), (3.16)
де I – потік маси, тепла або імпульсу (I=dM/dSdt у випадку дифузії; I=dQ/dSdt у випадку теплопровідності; I=dK/dSdt – у випадку перенесення імпульсу); b – коефіцієнт пропорційності для відповідного процесу; dG/dx – градієнт фізичної величини (температура, концентрація, швидкість руху шарів рідини або газу), зміна якої з відстанню зумовлює виникнення відповідного потоку.
3.1.4. Тепловіддача
Тепловіддача від твердого тіла в рідину або газ при їх конвекційному перемішуванні пов'язана з теплопровідністю через прилеглий до поверхні тонкий шар неперемішуваної речовини. Оскільки градієнт температури пропорційний різниці температур поверхні і температури в об'ємі рідини або газу, рівняння тепловіддачі має вигляд закону тепловіддачі, встановленого Ньютоном:
dT/dt=– a(T– Ts) s, (3.17)
де T – температура тіла, Ts – температура навколишнього середови-
ща, а a - коефіцієнт тепловіддачі, s – площа поверхні. Коефіцієнт тепловіддачі залежить від механізму теплопередачі, площі тіла, що знаходиться в контакті із середовищем і теплових властивостей самого тіла. Спробуйте проінтегрувати рівняння (3.17) і отримати залежність температури від часу.
84
Рівняння (3.17) – приклад диференціального рівняння першого порядку, оскільки в нього входить тільки перша похідна невідомої функції T(t). З огляду на те, що безліч процесів, що відбуваються в природі, описуються диференціальними рівняннями, важливо уміти розв’язувати ці рівняння. Розглянемо рівняння першого порядку вигляду
dy/dx=g(x). (3.18)
У загальному випадку аналітичного розв’язку рівняння (3.18), вираженого через добре відомі функції, не існує. Крім того, навіть у тому випадку, коли аналітичний розв’язок все ж таки існує, необхідно представити цей розв’язок в графічному вигляді, щоб зрозуміти його характер. Наближені числові розв’язки за допомогою ЄОМ дозволяють розглядати і значно складніші рівняння, в яких рівняння (3.18) може виражати одну із крайових умов. Графічний інтерфейс сучасних математичних пакетів дозволяє відслідковувати всі стадії процесу тепло- і масоперенесення.
3.1.5. Диференційні рівняння конвекційного теплообміну
Конвекція завжди супроводжується теплопровідністю, оскільки при русі рідини або газу завжди відбуваються зіткнення і перемішування частинок з різними енергіями. Рівняння перенесення енергії записують з урахуванням конвекційного теплообміну [1,2]
R |
R |
R |
R |
|
q |
= qтеплов + qконв = -kÑТ + rwh , |
(3.19) |
||
де h – питома ентальпія (в розрахунку на одиницю маси), w – |
вектор |
|||
локальної швидкості руху рідини. |
|
|
||
Згідно (3.19) проекції теплового потоку на координатні осі Ох, Оу, Oz складають:
qx = -k(¶T /¶x) + rwxh , qy = -k(¶T /¶y) + rwy h ,
qz = -k(¶T /¶z) + rwzh .
Зумовою балансу теплоти замість (3.15) отримаємо:
cr ∂T = kÑ2T - r(wx |
∂h + wy |
∂h + wz |
∂h ) - rh div(w) + rqρ . (3.20) |
|
|
|
|
|
R |
¶t |
¶x |
¶y |
¶z |
|
Для нестискуваних рідин (r=Const) згідно рівнянню нерозривності
R |
(3.21) |
div ( w ) = (дwx/дx)+(дwy/дy)+(дwz/дz) = 0. |
85
Рівняння руху.
Виділимо в потоці в'язкої рідини елементарний об'єм з ребрами dх, dy і dz. Припустимо, що швидкість змінюється лише в напрямку х, причому закон зміни швидкості довільний. Сили, що діють на даний елемент рідини, можна розділити на масові (або об'ємні) і поверхневі. Якщо у якості об'ємних сил враховувати тільки силу тяжіння, то на об'єм dV діє сила df1=rgdV.
Рівнодіючу сил тиску за напрямком х, вочевидь, можна знайти таким чином:
df2=Pdydz –(P + (dP/dx)dx)dydz=–(dP/dx)dV.
Аналогічно знайдемо рівнодіючу сил тертя, що діють на 2 бічні площинки об'єму dV, віддалені на dу одна від одної;
df3=fтр|y+dy–fтр|y=h(dwx/dy)y+dydxdz–
h(dwx/dy)ydxdz=h(д2wx/дy2),
де h – коефіцієнт в'язкості. При записі df3 враховано, що швидкість потоку збільшується з координатою у і сила fтр співпадає з напрямом руху. Підсумовуючи сили і враховуючи другий закон Ньютона (df=rdV(dwx/dt) )отримаємо рівняння руху
rdV(dwx/dt) =rgx– (dP/dx)+h (д2wx/дy2).
У загальному випадку тривимірного руху нестискуваної рідини з постійними фізичними параметрами поле швидкостей описується трьома рівняннями руху Навье-Стокса. Їх векторний запис лаконічніший,
r(d w /dt) =r g – Ñ P+h Ñ2 w . |
(3.22) |
Наближення постійної щільності (r = Const) у середовищі з неоднорідною температурою і тиском є поганим. Врахуємо залежність
щільності від температури, r = rо(1– b(Т– То)). Член ro g можна пред-
→
ставити як градієнт гідростатичного тиску Ñ Р' у нерухомій рідині зі щільністю rо. Після ділення лівої і правої частин рівняння (3.22) на r отримаємо наступне рівняння руху:
(d w /dt) =– g b(Т– То) – (1/ρ) Ñ (P- Р') + uÑ2 w . |
(3.23) |
де u=h/r – кінематична в'язкість.
86
Оскільки в (3.23) окрім wx, wy, wz і T невідомим є тиск Р′, еквівалентну (3.23) систему рівнянь (для трьох осей) слід розв’язувати спільно з рівнянням безперервності (3.21).
Форма і розміри граничної поверхні істотно впливають на характер руху рідини і тепловіддачу. Відомо, що є два основні режими течії рідини: ламінарний і турбулентний. За ламінарної або, інакше кажучи, "шаруватої" течії рідини можна виділити трубки струму, які рухаються не перемішуючись; при турбулентній течії має місце перемішування, безладна зміна напрямку і значень швидкості частинок рідини. Ці режими течії спостерігаються і в приграничному шарі між рідиною і твердою поверхнею. Якщо температурне поле знайдене з урахуванням руху рідини, то коефіцієнт тепловіддачі може бути знайдений з формули (3.17).
Безрозмірні змінні, числа подібності і рівняння подібності.
Спроби аналітичного вирішення повної системи рівнянь конвекційного теплоперенесення стикаються із серйозними труднощами. Тому є важливими експериментальні дослідження натуральних або модельних об'єктів. За допомогою їх можна знайти числові значення шуканих змінних і потім підібрати рівняння, що описують результати дослідів, в подібних умовах. Вирішити питання про те, чи можна результати, що отримуються за допомогою якої-небудь конкретної установки (моделі), перенести на інші аналогічні процеси, допомагає теорія подібності. Теорія подібності розвинена в роботах М.В.Кирпічева [3], А.А.Гухмана [4], М.А.Міхєєва[5].
Рівняння руху і теплопровідності прийнято записувати для безрозмірних величин [2-4]: X=x/lo, Y=y/lo, Z=z/lo, Wx=wx/wo,
Wy=wy/wo, Wz=wz/wo, θ=( Tгр -T)/( Tгр -To). Крім безрозмірних коор-
динат, швидкостей і температур в рівняння як коефіцієнти входять безрозмірні комплекси [2-4]:
Re=wolo/υ – число Рейнольдса;
Nu= αlo/κ - число Нусельта (безрозмірний коефіцієнт тепловіддачі);
Pe= wolo/αT - коефіцієнт Пеклі (співвідношення теплоти, що переноситься конвекцією, і теплоти, що передається теплопровідністю), Pe= Re Pr, где Pr=υ/αT – число Прандтля;
Gr=gβ( Tгр -To )lo3/υ2 – число Грасгоффа (характеризує підйомну силу, що виникає в рідині унаслідок неоднорідності щільності).
Безрозмірні величини θ, Wx, Wу , Wz ,X , У, Z, Nu , Pe, Re, Gr можна розглядати як нові змінні. З них незалежними є безрозмірні коор-
87
динати, залежними - величини θ, Wx, Wу , Wz , Nu. Для їх знаходження потрібно знати постійні Ре , Re , Gr для конкретної задачі.
3.1.6. Алгоритм Ейлера для розв’язку диференціальних рівнянь
Типовий метод чисельного розв’язку диференціальних рівнянь включає перетворення диференціального рівняння в звичайнорізницеве. Проаналізуємо рівняння (3.18). Покладемо, що при х = x0 функція у приймає значення y0. Оскільки рівняння (3.18) описує зміна функції у в точці x0, то можна знайти наближене значення функції у у довколишній точці x1 = x0 + x, якщо приріст аргументу х малий. У першому наближенні передбачається, що функція g(x), або швидкість зміни у, постійна на відрізку від x0 до х1. В цьому випадку
наближене значення функції у в точці х1 = x0 + |
x визначається вира- |
|
зом |
|
|
y1=y(x0) + y =y0 + g(x0) |
x. |
(3.24) |
Можна повторити цю процедуру і знайти значення у в точці х2=х1+ x
y2 = y(x1+ x) = y1 + g(x1) x. |
(3.25) |
Це правило можна узагальнити і обчислити наближене значення функції в будь-якій точці хn = x0 + n x по ітераційній формулі
yn = yn–1 + g(xn–1) x (n= 0, 1,2,...). |
(3.26) |
Даний метод називається методом дотичних, або методом Ейлера. Метод даватиме добре наближення до «дійсного» значення функції
у, якщо приріст аргументу |
x достатньо малий. У методі |
Ейлера |
|||
передбачається, |
що швидкість зміни функції у на відрізку |
від |
|||
хn–1 , до |
хn постійна, а |
нахил дотичної обчислюється |
в |
по- |
|
чатковій |
точці |
відрізка. У разі, коли нахил дотичної змінюється на |
|||
деякому відрізку, з'являється відхилення від точного рішення. Це відхилення можна зменшити, якщо вибрати менше значення x.
3.2. Крайові задачі
Рівняння тепло- і масоперенесення застосовні для опису найрізноманітніших фізико-хімічних і технологічних процесів. Це диференціальні рівняння другого порядку в частинних похідних. Але аналітичний розв’язок можливий тільки для спрощених граничних умов – постійних в часі, заданих на поверхнях тіл простої форми, наприклад, кулі або циліндра.
88
3.2.1. Крайові умови
Для однозначного розв’язку диференціальних рівнянь теплопровідності або дифузії повинен бути відомий ряд умов на межах прос- торово-часової області. Початкові умови визначаються завданням розподілу температури в початковий момент часу, тобто при t=0,
T(x,y,z,0) = To(x,y,z), |
(3.27) |
де To(x,y,z) – відома функція.
Гранична умова може бути задана різними способами.
Гранична умова першого роду (граничне завдання Діріхле) полягає в завданні розподілу температури на поверхні твердого тіла у будь-який момент часу, тобто
Tгр = Tгр(x,y,z,t) . |
(3.28) |
Гранична умова другого роду (гранична задача Неймана) полягає в завданні потоку через кожен елемент граничної поверхні як функції його координат і часу, тобто
qгр = qгр(x,y,z,t) . |
(3.29) |
Гранична умова третього роду полягає в задаванні температури навколишнього середовища Тc і закону теплообміну між поверхнею і навколишнім середовищем. Якщо тепловтрата визначається законом охолоджування Ньютона, то рівність теплоти, що підводиться до поверхні з об'єму зразка, і кількості тепла, що втрачається з неї,
q=–κ(дT/д n )гр=αк(Тгр–Тс) |
(3.30) |
відповідає формулюванню граничної умови третього роду. В умовах, коли істотний теплообмін променистою енергією, тепловий потік з поверхні необхідно записати у вигляді суми:
q=–κ(дT/д n )гр=αк(Тгр–Тс) +Cn[Тгр/100 –Тс/100] |
(3.31) |
де αк – коефіцієнт конвекційного теплообміну, а Cn – приведений коефіцієнт випромінювання.
Граничні умови четвертого роду відповідають теплообміну дотичних середовищ, коли температури дотичних поверхонь однакові. Така гранична умова задається співвідношеннями
Тгр,1= Тгр,2; |
|
–κ(дT1/д n )гр=–κ(дT2/д n )гр |
(3.32) |
89
Диференціальне рівняння нестаціонарної дифузії співпадає за виглядом з рівнянням теплопровідності. Для визначення концентраційних полів в різні моменти часу потрібно вирішувати рівняння (3.7) сумісно з початковими – при t=0, і граничними умовами. Останні можуть бути умовами першого, другого або четвертого роду (див. умови для теплового завдання (3.28), (3.29) і (3.32)). Для замкнутої системи на зовнішніх межах потоки речовини відсутні, і головним є правильний облік граничних умов на внутрішніх, наприклад міжфазних, межах.
3.2.2. Крайова задача в безрозмірних змінних |
|
Система рівнянь: |
|
ρсρ(дT/дt)=div(κgradT) +ρqρ; |
(3.33) |
при t=0 T=To(x,y,z); |
(3.34) |
–κ(дT/д n )гр=αк(Тгр–Тс) +Cn[Тгр/100 –Тс/100]; |
(3.35) |
cρ=cp(T); κ=κ(T); ρ=ρ(T), |
(3.36) |
у якій гранична умова третього роду в окремих випадках Тгр=Тс або при відомому qгр(x,y,z) зводиться до умов першого або другого роду, є нелінійною. Її рішення до теперішнього часу в загальному вигляді не знайдене. Тому набуває особливого значення використання принципу подібності, який дозволяє тільки на основі формулювання задачі отримати ряд важливих наслідків.
Для переходу до безрозмірних змінних застосовують лінійні пе-
ретворення: l=lol1, T=ToT1, κ=κoκ1, ρ=ρoρ1, сρ,1=сρ,oсρ,1, qρ,1= qρ,oqρ,1, де
величини з індексних «о» є масштабними, а з індексом «1» – безрозмірними. Крайова задача набуває вигляду
ρ1сρ,1(дT1/дF)=div(κ1gradT1) +ρ1qρ,1;
при F=0 |
T1=To,1(x1,y1,z1); |
||
–κ1 (дT1/д n )гр= Bik (Тгр,1–Тс,1) + Bo[Тгр,1/100 –Тс,1/100]; |
|||
κ1=κ1(T1), ρ1=ρ1(T1), сρ,1=сρ,1(T1). |
|||
Po= |
ρoqρolo2 |
– Померанцева; |
|
κ T |
|
||
|
o o |
|
|
Bik=αкlo/κ1 – Біо;
90
