Ovru-all

7.3.2. Досягнення рівноважного стану та вимірювання макроскопічних величин

Під час моделювання за методом МД процес встановлення рівноваги часто займає левову частину від загального часу розрахунку. Як правило, в початкових умовах зручніше за все вибирати «рівноважну» конфігурацію з якого-небудь колишнього розрахунку, яка відповідає температурі і густині, близькій до тих параметрів, що вимагаються. Молекулярна динаміка розвиває молекулярну конфігурацію кінцевого розміру, змінюючи її в часі крок за кроком. Є межі для типових часових рамок і масштабів довжини, які можуть бути досліджені.

Виконувані при моделюванні 103÷105 кроків за часом (≤10– 15с) алгоритму MД, звичайно відповідають декільком наносекундам реального часу. Необхідно перевірити, чи була в системі досягнута рівновага перш, ніж обчислювати середні значення величин. Крім того, потрібно піддати результати моделювання статистичному аналізу, зробити реалістичну оцінку похибок. Як довго потрібно проводити розрахунок? Це залежить від системи й фізичних властивостей, що становлять інтерес.

Припустимо, що нас цікавить змінна a, визначена так, що <a>=(1/N) ∑ ai =Const в рівноважному стані (наприклад, aі – це

i

швидкість і-го атому). Введемо часову функцію кореляцій значень a

– ∑ ai (t0) ai (t0+t), що зв'язує значення, обчислені через проміжки

i

часу t. Позначимо її як <a(t0)a(t0+t)>. Якщо стан системи рівноважний, ця функція не залежить від вибору початку відліку часу й тому можна її записувати у вигляді <a(0)a(t)>. Зрозуміло, що <a(0)a(0)>=<a2>. У разі великого часу t

232

Рівноважний макростан характеризується декількома параметрами, такими як, наприклад, абсолютна температура Т і середній тиск Р, а також об'ємом V й повною енергією E.

Кінетичне визначення температури випливає з теореми про рівнорозподіл: кожний квадратичний член, що входить у вираз для енергії класичної системи, що знаходиться в рівновазі за температури Т, має середнє значення ½kBT. Звідси можна визначити температуру Т системи в d-вимірному просторі співвідношенням

в якому сума береться за всіма N частинками системи й d компонентами швидкості. Дужки < > означають усереднення за часом. Вираз (7.42) є прикладом зв'язку макроскопічної величини, в даному випадку температури, із середнім за часом по траєкторіям частинок (миттєва кінетична енергія системи флуктуює). Співвідношення (7.42) справедливе у такому вигляді в тому випадку, якщо швидкість руху центру мас системи дорівнює нулю.

Ще однією тепловою характеристикою системи є теплоємність при постійному об'ємі СV=(∂Е/∂Т)V, СV – це міра кількості тепла, необхідного для зміни температури на 1 К. Оскільки теплоємність залежить від розмірів системи, зручно визначити питому теплоємність на частинку, а саме cV =СV/N. Легше за все отримати cV шляхом знаходження середньої потенціальної енергії та середньої повної енергії при близьких температурах Т й Т + Т. Температурна залежність cV зумовлена температурною залежністю потенціальної і кінетичної енергії, остання прямо пропорційна температурі ~(d/2)kBT.

Метод визначення тиску на основі теореми про віріал сили описано у підрозділі 7.1.4. У лабораторній роботі № 13 (у допоміжному посібнику) тиск визначається через імпульси молекул, що перетина-

ють межі основної комірки. Розглянемо елемент поверхні A і припустимо, що середня кількість руху, що перетинає в одиницю часу поверхню зліва направо, буде К+, а К– – середня кількість руху, що перетинає поверхню справа наліво. Тоді середня сила F рівна F = 0.5(К+ + |К– |), а середній тиск визначається виразом

234

де vі(0) й vi(t) – вектори швидкостей в початковий момент часу й у моменти часу t, ... – дужки статистичного усереднення за всіма

частинкам системи.

Динаміку атомів можна характеризувати спектром коливань атомів g(ω), отриманим з Фур’є перетворення АФШ

Для графічного відображення відокремлюють дійсну частину з рівняння (7.47)

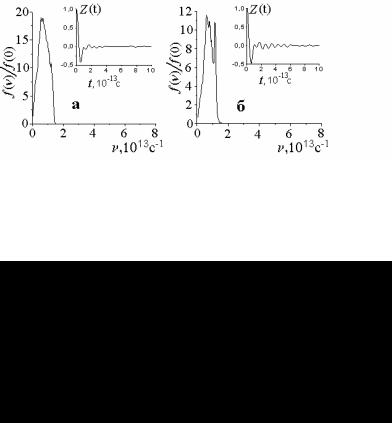
Рис. 7.16. Автокореляційні функції швидкості та їхні спектри в системах чистого заліза з нанокристалами різного розміру [105], Т=300 К

а – малі нанокристали (@350 атомів), b – великі нанокристали (³2000 атомів)

За виглядом залежності функції Z ( t ) , а саме за її затуханням, можна судити про динамічну релаксацію в матеріалах. На графіках рис. 7.16,а,б видно, що час динамічної релаксації в матеріалах з нанокристалами різного розміру відрізняється. У випадку зразків з нанокристалами малого розміру (рис. 7.16,а) й аморфних зразків осциляційний характер АФШ й їх спектри майже не відрізняються. Для атомів у цих зразках характерні неузгоджені коливання. У випадку зразків з нанокристалами великого розміру осциляції АФШ затухають повільніше, а у спектрах спостерігається чітке роздвоєння максимуму (рис. 7.16.,б). Нижче, на рис. 7.30, наведені інші данні, які

236

де |ri(t)-ri(0)| – модулі зміщення атомів, а функція δ[r−|ri (t) − ri (0)|]дорівнює одиниці у випадках, коли |ri(t)-ri(0)| належить інтервалу від r до r+ r, інакше ця функція дорівнює нулю.

Зрозуміло, що залежність середньоквадратичного зміщення частинок від часу визначається характером функції Gs (r,t):

Вважають, що функція Gs(r,t) частково підпадає під закон розподілу Гауса, й вивчають, якою мірою ця функція відхиляється від розподілу Гауса на всьому інтервалі значень (r,t). Більше інформації про функції Ван-Хова можна знайти в оглядах [57,58].

7.3.4. Топологічний аналіз змодельованих атомних конфігурацій. Метод Вороного-Делоне

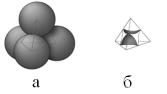
Сучасне дослідження структури потребує математичного підходу для вивчення взаємного розташування молекул у просторі, не опираючись ні на хімічні зв'язки, як при вивченні структури окремих молекул, ні на принципи й властивості трансляційної симетрії, які розроблені в кристалографії. Подібний підхід вже давно був розроблений математиками [59,60]. Одним з головних його творців був Г.Ф.Воронов. Б.Н. Делоне пояснив суть робіт Вороного й узагальнив основні теореми [60]. Бернал вперше застосував метод Вороного до дослідження структури рідини [61]. Вихідною геометричною побудовою, на якій базується метод, є так званий багатогранник Вороного – область простору, найближча до даного атома. Для його визначення посередині відрізків, проведених до найближчих атомів, будуються перпендикулярні до них площини (див. рис. 7.17,a). Фактично це комірка Вігнера-Зейтца. Форма багатогранників Вороного залежить від конкретного розташування сусідів навколо даного атома. Побудова багатогранників Вороного дозволяє перейти від переліку (файлу) координат атомів до геометричних образів. На рис. 7.18 показані багатогранники Вороного деяких тривимірних упакувань куль. Для простих кристалічних структур існує свій єдиний багатогранник, що відбиває найближче оточення, однакове для всіх атомів даного кристалу. У неупорядкованій фазі багатогранники Вороного, природньо розрізняються для різних атомів, але вони мають характерні риси, які відповідають структурі даної системи У сучасних роботах з моделювання показано, що в аморфних фазах досить велика доля кластерів, утворених ікосаедрами (20-гранник, утворений з трикутникових пірамід, рис. 7.18,д), для яких

238

просторі – тетраедр. Їхня форма визначається конкретним розташуванням атомів і може служити характеристикою структури системи.

Рис.7.19. Ілюстрація симплекса Делоне в

3-вимірному просторі;

а – симпліцільна конфігурація атомів; б – порожній простір між атомами,

що визначає елементарну (симпліцільну) пору.

Крім вивчення структурних характеристик, розбивка ВороногоДелоне дозволяє приступити до вивчення порожнеч між атомами. Цей аспект досліджень є навіть важливішим, ніж аналіз закономірностей у розташуванні атомів самих по собі. Багато важливих фізичних процесів, наприклад, дифузія домішок, протікання дрібних атомів через гранульовані пористі матеріали зв'язані напряму саме з міжатомними порожнечами. Симплекс Делоне визначає відносно велике вільне місце між атомами, куди ведуть, як правило, більше вузькі порожнечі (рис. 7.18 та 7.19). З геометричної точки зору кожен симплекс Делоне визначає елементарну порожнину в системі атомів.

Для невпорядкованих і термічно збурених систем симплекси Делоне є викривленими тетраедрами. Використовуючи кількісну міру форми симплексу, автори [62] виділяли ті атомні конфігурації, які ближче до досконалого тетраедра. Саме такі симплекси характерні для щільної кристалічної структури. Вони зустрічаються і в рідкій фазі, проте характер їх взаємного розташування принципово відрізняється від кристалічного. Питання щодо аналізу структури модельованих систем методом Вороного-Делоне докладно розглянуті в книзі [63].

7.4.Проблема вибору потенціалів

7.4.1.Потенціали міжатомної взаємодії в металах

При побудові моделей речовини методами МД і Монте-Карло виникає необхідність застосування потенціалів міжатомної взаємодії. У підрозділі 1.2.5 були розглянуті деякі потенціали міжатомної взаємодії, які застосовують для моделювання, кристалів інертних газів (парний потенціал Леннарда-Джонса) і напівпровідникових речовин Si, C, Ge (трьохчастинкові потенціали Стілінджера-Вебера, Терзоффа).

240