
Ovru-all
.pdfПритому в системі порівняння щільності цієї властивості xα=Хα/Vα,
xβ=Хβ /Vβ залишаються незмінними аж до розділяючої поверхні. Для будь-якої екстенсивної властивості реальної двофазної системи справедливий вираз
zβ
X = ω ∫ x(z)dz ,
zα
де zα, zβ – координати межі фаз; x(z) – функція, що дає залежність локальної щільності цієї властивості від нормальної до поверхні координати z . Зокрема, для загального числа частинок в двокомпонентній системі маємо:
zβ
N = ω ∫ n(z)dz .
zα
Для адсорбції i-го компонента запишемо
0 zβ
Γi = Niω /ω = ∫[ni (z) − niα ]dz + ∫[ni (z) − niβ ]dz ,
zα |
0 |
А для будь-якої зведеної надлишкової термодинамічної величини
0 |
z β |
|
X ω (z = 0) = ∫[x(z) − xα ]dz + ∫[x(z) − x β ]dz . |
(5.21) |
|
zα |
0 |
|
Вираз (5.21) записаний для випадку, коли розділяюча поверхня знаходиться в положенні з координатою z=0. Перемістимо в думках цю поверхню на відстань z у бік фази β (рис. 5.6). Тоді для надлишкової властивості щодо нового положення розділяючої поверхні вираз (5.21) перепишеться так:
zzβ
Xω (z = z) = ∫[x(z) − xα ]dz + ∫[x(z) − xβ ]dz .
|
zα |
z |
|
Отриманий вираз легко перетворити: |
|
|
|
0 |
zβ |
z |
|
Xzω= z = ∫[x(z) − xα ]dz + ∫[x(z) − xβ ]dz + ∫ x(z) − xα − (x(z) − xβ )dz |
|||
zα |
0 |
0 |
|
або |
|
|
|
Xzω= z |
= Xzω=0 − (xα − xβ ) |
z. |
(5.22) |
Таким чином, залежність надлишкових термодинамічних властивостей від нормальної координати z, у разі плоскої поверхні розділу,
151
лінійна. Це дозволяє зафіксувати розділяючу поверхню, залежно від розглядуваної задачі, щодо будь-якої надлишкової властивості.
Рис.5.7. Різні положення розділяючої поверхні, використовувані при
обчисленні адсорбції.
5.2.6. Різні способи вибору розділяючої поверхні
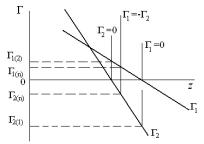
Практично цінним і найбільш важливим результатом термодинамічної теорії Гіббса є отримане вище адсорбційне рівняння: (5.20). Як показано вище, sω и Гi, є лінійними функціями нормальної координати z, що характеризує положення розділяючої поверхні між співіснуючими фазами. На рис. 5.7 приведені графіки адсорбції компонентів в бінарній системі. З цього малюнка видно, що величина адсорбції компонентів залежить від того, де ми розташуємо розділяючу поверхню. Отже, безглуздо говорити про величину адсорбції, поки однозначно не визначено положення розділяючої поверхні.
З математичної точки зору, положення розділяючої поверхні може бути будь-яким, тобто рівняння (5.22) справедливе при будьякому положенні розділяючої поверхні. Проте, як відзначав сам Гіббс, з фізичної точки зору зручніше розташувати розділяючу поверхню в області неоднорідності, тобто усередині поверхні розриву, або не дуже віддалено від неї. На коректність такого вибору вказує і те, що поверхневий натяг приписується цій розділяючій поверхні.
Гіббс запропонував обчислювати адсорбцію компонентів щодо розділяючої поверхні, проведеної так, щоб адсорбція одного з компонентів дорівнювала нулю, Гj=0. Адсорбцію компонентів щодо цієї поверхні називають відносною адсорбцією Гіббса і позначають Гi(j). Індекс j підкреслює, що адсорбція j -го компоненту на цій поверхні рівна нулю.
Пізніше, аналізуючи адсорбційні явища в рідких розчинах, Гуггенгейм і Адам запропонували інший спосіб вибору розділяючої по-
152
верхні. Як видно з рис. 4, поблизу поверхні розриву завжди можна знайти таке положення розділяючої поверхні, що виконується
k
умова ∑Γi = 0 . У літературі адсорбцію щодо цієї поверхні нази-
i=1
вають N - варіантом адсорбції по Гуггенгейму і Адаму і познача-
ють Гi(n) (см. рис.5.7).
Гуггенгеймом і Адамом запропоновані і інші способи визначення адсорбциі, (див. у [2]). Зокрема, запропоновано обчислювати адсорбцію щодо розділяючих поверхонь, які відповідають умовам
k |
|
k |
ΓiVi = 0 , де Mi – молярна маса, а Vi - парціаль- |
∑Γi M i = 0 |
або |
∑ |
|
i=1 |
|
i=1 |
|
k
ний молярний об’єм i-го компонента. Варіант ∑ Γiμ i = 0 був би
i=1
зручний для багатьох задач, проте абсолютні значення μi, як правило, невідомі. Пропонувалися ще варіанти визначення z такі, що uω=0 або sω=0. Проте при розгляді адсорбційної рівноваги в багатофазній системі найбільш зручним варіантом вибору положення розділяючої поверхні є варіант, запропонований Гіббсом, тобто краще розглядати величини Гi(j).
5.2.7. Адсорбційна рівновага в багатокомпонентних системах
Якщо фази α і β, розділені плоскою межею, знаходяться в стані термодинамічної рівноваги, то виконуються умови: Рα= Рβ, Тα= Тβ,
μіα= μіβ. При малих зсувах уподовж кривих рівноваги фаз на діаграмах стану справедливі також співвідношення:
dРα= dРβ, dТα= dТβ, dμіα= dμіβ. |
(5.23) |
Згідно співвідношенням Гіббса-Дюгема, запишемо для кожної з фаз:
α α α k α μα
dР = s dТ + ∑ ni d i ,
i=1
β α k β μβ
dРβ = s dТ + ∑ ni d i .
i =1
На підставі цих співвідношень запишемо співвідношення ГіббсаДюгема для рівноважної двофазної системи
k |
|
(sα – sβ)dТ+ ∑(niα − niβ )dμ i =0. |
(5.24) |
i=1
153
Таким чином, для рівноважної двофазної системи можна розглядати разом рівняння (5.19) і (5.24).
Виразимо dμj із (5.24):
|
|
|
|
|
k |
|
|
|
|
− nbj ). |
|
–d μj= dТ (sa – sb)/(nja – njb)+ ∑(nia − nib )dμ i |
/(naj |
(5.25) |
|||||||||
|
|
|
|
|
i=1 |
|
|
|
|
|
|
Підставляючи ( 5.25 ) в ( 5.19 ) маємо: |
|
|
|
|
|
|
|||||
|
s |
α |
− s |
β |
k |
|
|
α |
β |
|
|
– dγ= [s ω –Γj |
|
|
] dТ+ ∑[Γi |
− Γj |
ni |
− ni |
]dμi . |
(5.26) |
|||
|
α |
|
β |
n |
α |
− nβ |
|||||
|
|
|
i 1 |
|
|
|
|||||
|
n j |
− n j |
= |
|
|
j |
j |
|
|
||
У отриманому виразі dγ є повним диференціалом. Отже, коефіцієнти при dТ і dμi у цьому рівнянні є частинними похідними по температурі і хімічному потенціалу:
sω –Γj |
s |
α − sβ |
= −(dγ /dT ) |
; |
|
|
(5.27) |
||||||
nαj − nβj |
|
|
|||||||||||
|
|
|
|
|
i |
|
mi |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Γ − Γ |
|
na |
− nb |
= −(dγ /dμ |
|
) |
|
|
|
|
|
||
|
|
i |
i |
|
|
|
|
|
. |
(5.28) |
|||
j na |
− nb |
|
T,mk |
(i¹ j) |
|||||||||
i |
|
i |
|
|
|
||||||||
|
|
|
j |
j |
|
|
|
|
|
|
|
|
|
Як показано вище, поверхневий натяг плоскої поверхні розриву не залежить від положення розділяючої поверхні, отже, не повинні залежати від положення розділяючої поверхні і похідні (5.27) і (5.28).
Неважко довести, що чисельне значення коефіцієнтів при dТ і dμi в рівнянні (5.26) співпадають із значеннями відповідних величин відносно розділяючої поверхні, що задовольняє умові Гj=0. Дійсно,
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Γj |
|
|
=z(Гj=0) – |
відстань від вибраного положення розділяючої |
||||||||||||
nαj − nβj |
|
|||||||||||||||
поверхні до положення поверхні, що відповідає умові Гj=0. Тоді |
||||||||||||||||
|
|
Γ − Γ |
|
nα |
− nβ |
= Γ − z |
|
|
|
α − nβ ) = Γ |
|
|
||||
|
|
|
i |
i |
|
=0) |
(n |
. |
(5.29) |
|||||||
|
|
j nαj − nβj |
|
|||||||||||||
|
|
|
i |
|
i |
(Ã j |
i |
i |
i( j) |
|
|
|||||
Аналогічно |
|
|
sα − sβ |
|
|
|
|
|
|
|
|
|||||
|
|
|
sω –Γj |
|
|
|
(nα |
− nβ ) = sω( j) . |
|
|||||||
|
|
|
|
|
= sω − z |
(Ã j |
=0) |
(5.30) |
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
nαj − nβj |
|
i |
|
i |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отже, вибір при описі адсорбційних процесів такої поверхні, що відносно неї адсорбція певного (j-го ) компонента Гj=0, рівносильний врахуванню умови рівноваги поверхні розриву і співіснуючих фаз. Істотно, що знайдені з експериментальних даних похідні від γ
154
(5.27) и (5.28) ) дозволяють знайти саме такі відносні значення s ω и Гi(j). Щодо інших розділяючих поверхонь адсорбцію можна перерахувати, згідно з (5.22).
5.2.8. Обчислення адсорбції у двокомпонентних системах
Простим об'єктом для застосування адсорбційного рівняння Гіббса є двофазна двокомпонентна система, для якої маємо:
-dγ= [sω –Γ2j |
sα − sβ |
]dТ+[Γ1 − Γ2 |
niα − niβ |
]dμ i |
(5.31) |
|
nαj − nβj |
||||
nαj − nβj |
або
-dγ= s(2)ω dТ+ Г1(2).
Відповідно маємо
s(2)ω = −(dγ /dT)μ1 , Г1(2) = −(dγ /dμ1 )T
Якщо експериментально або теоретично визначена залежність поверхневого натягу від хімічного потенціалу і температури, то з останніх співвідношень можна визначити густину надлишкової ентропії і числа частинок або, згідно введеної термінології, поверхневу ентропію і відносну адсорбцію Гіббса.
У отриманих виразах як незалежна змінна використаний хімічний потенціал, що не зовсім зручно, у зв'язку з тим, що хімічний потенціал безпосередньо з експериментів не визначається. Тому перейдемо від хімічних потенціалів до молярних доль і коефіцієнтів термодинамічної активності. Для цього скористаємося відомим виразом для хімічного потенціалу:
μi=μi0 + RTlna i= μi0 +RTlnfixi ,
де a i=fixi – термодинамічна активність, |
fi - коефіцієнт термодина- |
||||||||||||||||||
мічної активності. Очевидно, що при |
T=Сonst , |
|
|
||||||||||||||||
|
|
dμi= RTlna i =RT(dai/ai) . |
|
|
|||||||||||||||
Тоді для адсорбції по Гіббсу |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Г1(2) = −(dγ /dμ |
1 |
) |
|
= − |
a1 |
(∂γ /∂a ) |
= − |
|
f1x1 |
(∂γ /∂( f x )) . |
|||||||||
T |
|
|
|
||||||||||||||||
|
|
|
|
RT |
|
|
|
1 T |
|
|
|
|
RT |
1 1 |
T |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Враховуючи, що da1=( x1(дf1/дx1) + f1) dx1, запишемо для адсорбції |
|||||||||||||||||||
|
|
|
|
|
|
|
f1x1 |
|
|
|
|
|
|
∂γ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г1(2) = − RT(x (∂f |
|
/∂x ) + f |
|
|
|
∂x |
(5.32) |
||||||||||||
1 |
1 |
) |
. |
||||||||||||||||
|
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
T |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
155 |
Для слабкого розчину, близького до ідеального, f1 1, тому
Г1(2) = − |
x |
1 |
|
∂γ |
|
|
|
|
|
. |
(5.33) |
||
|
|
|
||||
|
|
|
|
∂x1 |
|
|
|
RT |
T |
|
|||
Цей вираз приводиться в багатьох підручниках із спрощеним описом адсорбції.
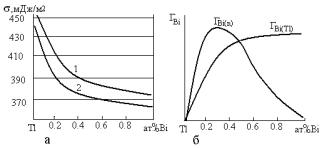
Розглянемо поверхневі властивості подвійного металевого розплаву талій - вісмут [4]. На рис.5.8 показана залежність поверхневого натягу і адсорбції вісмуту на межі розплав-газ від складу розплаву. Адсорбція розраховувалася, згідно (5.32), для двох положень розділяючої поверхні – спочатку по Гіббсу (пропорційно похід-
ній(dγ /dxBi )T ), потім для еквімолярної поверхні (n-варіант) по Гуггенгейму і Адаму.
Рис.5.8. Ізотерми поверхневого натягу і адсорбції системи Tl-Bi,
1 – 623 К, 2 – 773 К.
Як видно з рисунку, у всьому концентраційному інтервалі адсорбція вісмуту позитивна. Невеликі добавки вісмуту приводять до збільшення його адсорбції, При значних концентраціях вісмуту залежності адсорбції від концентрації по Гіббсу і по Гуггенгейму з Адамом істотно відрізняються.
156
Розділ 6 ПОВЕРХНЕВІ ПРОЦЕСИ ПІД ЧАС КРИСТАЛІЗАЦІЇ.
6.1. Поверхнева енергія та рівноважна форма кристалів
6.1.1. Поверхнева енергія в першому наближенні та її анізотропія.
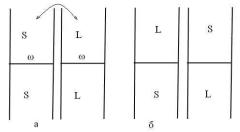
Як нам вже відомо, поверхневий натяг у разі однокомпонентних систем співпадає з вільною поверхневою енергією σ= F ω = u ω – Ts ω, де надлишкова внутрішня енергія і ентропія віднесені до одиниці площі. У разі вельми впорядкованої поверхні кристалів внесок ентропійного доданку є невеликим. Зробимо оцінку зміни енергії при утворенні поверхні згідно [1]. Дві окремі фази, наприклад кристалічну і рідку, розділимо умовною поверхнею (рис. 6.1).
Рис. 6.1. Гіпотетичне утворення міжфазної поверхні.
Розірвемо фази та, відповідно, зв’язки атомів ss та ll за виділеною поверхнею, пересунемо верхні частини і з’єднаємо їх з нижніми. При цьому виникають дві міжфазні межі, й утворюються нові зв’язки ти-
пу sl : 1 ss +1 ll → 2 sl. Тому зміна внутрішньої енергії на одиницю площі складе γ uω =ns εsl, εsl= Vsl – (Vss+Vll)/ 2, де ns – поверхнева
концентрація атомів, εsl – надлишкова енергія sl зв’язків в розрахунку на один зв’язок одного атома. Для оцінки поверхневої енергії межі кристал-розплав зазвичай використовують наближення Vsl Vll.
Тоді εsl (Vll – Vss)/ 2= H/z, де H – теплота (зміна ентальпії) фазового переходу, z – координаційне число. Теплота плавлення металів порівняно невелика, 8÷13 кДж/моль. Відповідно, в цьому випадку γ 0.1 Дж/м2. У випадку границі кристал-пара зв’язки поверхневих атомів ненасичені, εs = Vss ΔH/z, де H – теплота випаровування.
157
Теплоти випаровування металів DH = 100¸300 кДж/моль. Візьмемо DH = 166 кДж/моль. Для гранецентрованої кристалічної гратки z=12, e=DH/NA/12=2.3×10 –20 Дж; на кожний поверхневий атом грані (111)
припадають 3 некомпенсовані зв’язки і площа а2Ö3/8@4×10–20 м2 (а – параметр комірки кристалічної гратки). Тому в наближенні врахування зв’язків тільки з найближчими сусідніми атомами g111=8Ö3DH/(z а2)=2 Дж/м2. У молекулярних кристалів теплоти випаровування у 2-3 рази нижчі, ніж у металів, а міжмолекулярні відстані
– у 2-3 рази більші. Тому поверхневі енергії менші, ніж для границі кристал-пара метала у 20 ¸50 разів.
Рис. 6.2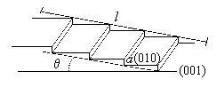
Поверхнева енергія g кристалів анізотропна. Значення g мінімальні для поверхонь, які збігаються зі щільно упакованими площинами кристалічної гратки (F-грані). Підрахуємо енергію поверхонь, слабко відхилених від F-граней. Такі поверхні називають віцинальними (від vicinus, лат. – близький). Віцинальна поверхня, показана на рис. 6.2, побудована з плоских терас висотою а та одиничної ширини. Запишемо сумарну поверхневу енергію виділеної ділянки поверхні дов-
жиною l, позначивши вільну поверхневу енергію F-граней як g010 та
g001,
gl = l sinq g010 + l cosq g001=
|
|
|
|
|
|
g010 |
|
|
|
g |
|
|
|
||
2 |
2 |
|
|
|
|
|
|
001 |
|
|
|||||
l g010 |
+ g001 sinθ |
|
|
|
|
|
+ cosθ |
|
|
|
|
= |
|||
2 |
2 |
2 |
2 |
||||||||||||
|
|
|
|
|
|
g010 |
+ g001 |
|
|
|
g010 |
+ g001 |
|
|
|
|
|
|
|
|
(sin θsin y + cos θcos y). |
|
|
||||||||
|
|
l g0102 + g0012 |
|
|
|
||||||||||
Уявімо прямокутний трикутник з катетами g010 та g001 та гіпотенузою

 g0102 + g0012 . Відношення катетів до гіпотенузи в останній формулі позначено як siny та cosy. У результаті маємо:
g0102 + g0012 . Відношення катетів до гіпотенузи в останній формулі позначено як siny та cosy. У результаті маємо:
|
|
|
|
g = l g0102 + g0012 cos(q –y). |
(6.1) |
||
158
Якщо γ010 =γ001, ψ=45°, і для цієї орієнтації γ приймає максимальне
значення (і ще для кутів 135, 225 і 315°). Отже, при зростанні кута θ орієнтації поверхні відносно орієнтації F-грані, поверхнева енергія
збільшується. Але зростання θ з часом приведе до наближення орієнтації поверхні до орієнтації іншої F-грані і зменшення поверхневої енергії. Отже, для F-граней поверхнева енергія мінімальна. Якщо
такі мінімуми гострі, на залежності γ(θ) є особливі сингулярні точки, у яких похідні γ′(θ) зазнають розриву. Тому поверхні з орієнтацією
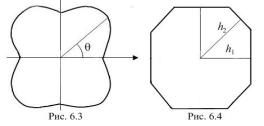
F-грані називають сингулярними. Залежності γ від орієнтації поверхні відображають за допомогою полярних діаграм. Такі діаграми тривимірні, оскільки орієнтації поверхні задаються двома кутами. На рис. 6.3 відображений двовимірний переріз полярної діаграми поверхневої енергії, побудований згідно з формулою (6.1), а на рис. 6.4 – рівноважна форма кристала, яка відповідає цій полярній діаграмі.
6.1.2. Рівноважна форма кристалів
Насправді, полярні діаграми набагато складніші [1], навіть в їхніх перерізах мінімумів більше. Знаючи полярну діаграму, можна побудувати рівноважну форму кристалів. З іншого боку, з експериментальних даних про рівноважну форму можна знайти полярну діаграму. Експерименти з визначення рівноважної форми дуже непрості тому, що кристал треба довго підтримувати у рівновазі із середовищем. Але кристал кінцевого розміру, що знаходиться у рівновазі із середовищем – це критичний зародок (див. р. 2.7), і рівновага ця нестійка. Габітус кристала визначається сукупністю граней, які він має. Рівноважна форма може складатися із граней і закруглених ділянок між ними. При підвищені температури часто відбувається розупорядкування поверхневої структури, поверхня кристала стає шорсткою в атомному масштабі. При цьому змінюється й полярна діаграма, на її мінімумах зникають гострі точки – зникає сингулярність. Відповідно, на рівноважній формі з’являються округлі ділянки. З подальшим
159
підвищенням температури грані зменшуються за площею і з часом зовсім зникають. Рівноважна форма стає круглою. А при відхиленні від рівноваги кристали ростуть у вигляді округлих дендритів.
Як показано Херінгом (див. у [1]), у разі довільної орієнтації по-
верхні, що задається кутами θ і ϕ, локальна рівновага ділянки кристала із середовищем (значення температур та концентрацій середовища у поверхні кристала, при яких має місце динамічна рівновага за кількістю частинок, що відриваються й приєднуються) визначається формулою
|
Ω |
|
|
∂2 γ |
|
Ω |
|
|
∂ 2 γ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μсер=μкр+ R |
|
γ + |
∂θ2 |
+ |
R |
2 |
|
γ + |
∂ϕ2 |
, |
(6.2) |
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
де R1 та R2 – радіуси кривизни поверхні у двох перпендикулярних перерізах, що містять у собі вектор нормалі до поверхні.
Згідно з Херінгом, рівноважну форму можна визначити з полярної діаграми поверхневої енергії як внутрішню огинаючу родини площин, дотичних до полярної діаграми у кожній її точці. Якщо, на полярній діаграмі є сингулярні мінімуми, то на рівноважній формі кристала обов’язково присутні грані, що відповідають цим сингулярним точкам, тому що площини, дотичні до полярної діаграми для значень поверхневої енергії з кутами, що відхилені від сингулярної точки, ніколи не належать до внутрішньої огинаючої.
6.1.3. Принцип Кюрі-Вульфа
Принцип Кюрі-Вульфа стосується кристалів з гарною огранкою. Згідно з ним, вільна поверхнева енергія для кристала, що знаходиться у рівновазі з навколишнім середовищем, має бути мінімальною
∑ γ iωi =0, |
(6.2) |
i |
|
ωі – площа і-ї грані. Виходячи з цього принципу Кюрі та Вульф дійшли висновку, що рівноважна форма кристала пов’язана з анізотропним поверхневим натягом таким чином, що відстані граней від центра кристала hі (рис. 6.4) пропорційні поверхневим енергіям гра-
ней γі.
Об’єм поліедра V= |
1 |
∑ hiωi . Для рівноважної форми об’єм ста- |
|
||
3 |
i |
|
|
|
|
лий (адже це – об’єм критичного зародку), диференціал від об’єму пов’язаний переважно зі зміною відстаней від граней до центра. Отже,
160
