
Ovru-all
.pdfBo= Cn To3lo/108 – Больцмана,
а замість часу - число Фур’є F= |
κot |
|
|
. |
|
ρocρolo2 |
||
Отримана безрозмірна система рівнянь (3.6-3.9) дозволяє зробити висновок про необхідні і достатні умови подібності температурних полів в процесі нестаціонарної теплопровідності. Температурні поля будуть подібними, якщо вони описуються тотожними рівняннями і умовами однозначності. Система (3.6-3.9) показує, що це досягається для геометрично подібних тіл за умови, що числа подібності, отримані в результаті лінійних перетворень, однакові.
3.3. Аналітичні розв’язки задач тепло- й масоперенесення при рості кристалів.
3.3.1. Задачі Стефана
Під назвою "задачі Стефана" об'єднаний цілий клас задач про перенесення, основаних на диференціальних рівняннях теплопровідності або дифузії з рухомою або вільною межею (дивись в [6,7]). Сам Стефан вивчав швидкість потовщення льоду в полярних морях. Теплота кристалізації льоду, що утворюється там, відводиться через шар твердої фази і відбирається холодним повітрям, що має температуру нижче за температуру замерзання води. З потовщенням шару льоду відводити теплоту від фронту кристалізації стає все важчим, завдяки чому потовщення крижаного покрову сповільнюється, що робить цей процес нестаціонарним. Головна складність викладеного завдання полягає в тому, що положення межі розділу фаз невідоме, воно залежить від часу і підлягає визначенню в ході розв’язку.
Згодом стефановськими почали називати всі задачі про перенесення тепла і речовини при зростанні кристалів, наприклад, задачі про потік тепла в перегрітому розплаві (вирощування кристалів по методах Бріджмена, Чохральського, Чалмерса);
задачі про потоки тепла в переохолодженому розплаві (вільне зростання кристалів, твердіння відливок);
задачі про дифузію речовини (зростання кристалів з розчину, пари в присутності інертного газу, розплаву у присутності домішки або
зрозчину в розплаві).
Утрадиційній постановці задач Стефана форма і температура фронту кристалізації вважаються заданими, а швидкість підлягає обчисленню. Модифіковане завдання Стефана, його називають зворот-
91
ним, передбачає розрахунок температури фронту кристалізації при заданих формі фронту і швидкості його переміщення. Найскладніший варіант задачі, мабуть, міститиме повний опис зростання кристала з визначенням форми, температури і швидкості фронту при заданих початкових температурних або концентраційних полях і відомих залежностях від локального поверхневого пересичення (переохолодження) швидкості росту.
3.3.2. Задача Стефана в чистому вигляді
Розв’язок задачі про направлену (з плоским фронтом зростання) кристалізацію перший опублікував Стефан, хоча відомі твердження, що спочатку її вирішив Нейман. Припустимо, що рідина у великому
об'ємі знаходиться при однаковій температурі Т∞>Тпл (Тпл – температура плавлення). Нехай у момент часу t=0 температура плоскої поверхні рідини миттєво знижується до температури Т = 0. Тоді рівняння теплопровідності в ізотропному кристалі і розплаві запишуться в лабораторній системі координат з віссю х, направленою по нормалі до охолоджуваної поверхні, таким чином:
|
(1/aрТ)(дTр/дt)= (д2Tр/дх2); |
(3.37) |
|
(1/aкТ)(дTк/дt)= (д2Tк/дх2); |
(3.38) |
Тут aТ - |
температуропровіднісгь (см2/с); aрТ |
= kр/(r×ср); aкТ= |
kк/(r×ск), |
де kр і kк – коефіцієнти теплопровідності рідкої і твердої |
|
(кристалічної) фази відповідно; r - їх щільність, а |
ср і ск – питомі |
|
теплоємності. Приймається, що температура поверхні розділу крис- тал-розплав з координатою х=X(t) дорівнює температурі плавлення
Тр(Х) = ТК(Х) = Тпл .
Умова балансу тепла на межі розділу фаз має вигляд |
|
kк(дTк/дх)х=Х –kр(дTр/дх)х=Х= Lr(дХ/дt), |
(3.39) |
де L- прихована теплота плавлення. Саме ця умова і вносить нелінійність до системи диференціальних рівнянь.
Решта граничних і початкових умов завдання наступна:
Тр ®Т∞ при х®¥; Тк ®Тповітря при х®0; Х=0 при t =0; Тр =Т∞ при t =0.
92
Користуючись міркуваннями розмірності, можна ввести безроз-
мірний параметр uр=x/ |
aTрt і переписати рівняння теплопровід- |
||
ності для рідини |
|
|
|
(д2Tр/дuр2)= –(uр/2)(дTр/дuр). |
(3.40) |
||
Вважаючи h=дTр/дuр, і проводячи інтегрування, знаходимо |
|
||
|
|
∞ |
|
h=С ехр(–uр2/4); Тр (uр) –Тр(¥)=– ∫ h(z)dz =–A1erfc(uр/2); |
|
||
|
|
uр /2 |
|
де A1 - постійна, a |
|
∞ |
|
|
|
|
|
1–erf (х)= erfc(х)=(2/ |
p |
) ∫ exp(-x2 )dx . |
|
x
Таким чином, розподіли температур виражаються формулами:
у розплаві Тр(х, t)=Т – A1erfc(x/2 |
aTt ); |
(3.41) |
|||||||
|
∞ |
|
|
р |
|
||||
|
|
|
|
|
|
|
|
|
|
у кристалі |
Тк (х, t)= B1erfc(x/2 |
aTк t ). |
(3.42) |
||||||
Враховуючи граничну умову при x=Х |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
B1erfc(X/2 aTt ) = Т – A1erfc(X/2 |
aTt ) =Тпл =Const |
(3.43) |
|||||||
к |
∞ |
р |
|
|
|
|
|||
отримаємо X(х, t). Отже, відстань X пропорційна |
|
, тобто |
|
||||||
t |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
X = 2l aTк t , |
|
|
|
|
|
(3.44) |
||
де l - константа, залежна від теплофізичних характеристик фаз і величини Т∞–Тпл. Враховуючи (3.44), можна отримати вираз для визначення l, а потім визначити постійні B1 і A1
B1=Тпл/erf(l), А1= (Т∞–Тпл)/(erfс(l) 
 aTк /aTр ).
aTк /aTр ).
З цими значеннями постійних формули (3.14) і (3.15) дають остаточні вирази для температури кристала і розплаву. Як випливає з чисельного прикладу, приведеного Паркером [6] з врахуванням теплофізичних параметрів води, для Тповітря = –5º С виходить, що за час Т=48×103 с утворюється шар льоду товщиною 1 см, а за 42 години – шар завтовшки всього 10 см.
Для того, щоб кристалізація йшла з постійною швидкістю, а не сповільнювалася з часом (зворотна модифікована задача Стефана),
необхідно температуру на поверхні х= 0 не підтримувати незмінною, а поступово знижувати.
93
3.3.3. Випадок переохолодженого розплаву
Нехай початкова температура всього об'єму розплаву нижче температури плавлення (Т∞–Тпл), а вже при t=0 починає утворюватися тонкий шар кристала, температура якого в усіх точках рівна Тпл, тому, що тепловідвід через кристал відсутній, і все тепло відбирається розплавом, який від цього нагрівається. При цьому виконується умо-
ва Тк = Тпл при 0£х£Х(t).
Розв’язуючи вищенаведену систему рівнянь (3.37), (3.38), (3.39) із зміненими граничними умовами, можна отримати
|
|
|
|
|
|
|
|
|
|
|
|
X = 2l |
|
apTt , |
(3.45) |
||||||
|
lL |
|
|
|
|
|
|
|||
|
p |
|
|
|
|
|||||
Тр(х, t) =Т + |
|
erfc(x/2 aTt ); |
(3.46) |
|||||||
cр exp(-l) |
||||||||||
∞ |
|
|
|
р |
|
|||||
де стала l знаходиться розв’язком рівняння |
|
|||||||||
l exp(l2) erfc(l) = (Тпл –Т∞) cр/(LÖp). |
(3.47) |
|||||||||
При розрахунку швидкості кристалізації отримуються приблизно такі самі результати, що і для випадку непереохолодженої рідини з тепловідводом крізь кристалічну фазу.
3.3.4. Краєві умови для дифузійної задачі росту кристалів
При зростанні кристалів концентраційні поля зазвичай нестаціонарні, їх слід знаходити із залежного від часу рівняння дифузії (другий закон Фіка (3.5))
(дC/дt)=div(DÑC)@DÑ2C, (3.48)
де друга рівність має місце, якщо коефіцієнт дифузії не залежить від концентрації.
На зовнішніх межах даних об'ємів потоки як правило відсутні. За винятком спеціальних випадків підживлення розчинів для таких меж достатнім є завдання початкового концентраційного поля C(x,y,z,t=0). Основну нелінійність вносять граничні умови на міжфазних поверхнях (поверхня кристала з навколишнім середовищем). Ці поверхні можуть мати складну форму, до того ж вони переміщаються. Тому граничні умови на цих поверхнях носять тільки локальний характер.
Умова балансу речовини на цих межах має вигляд
V(Cк – Сп) = D (дC/дn). |
(3.49) |
де Cк – концентрація в кристалі, а Сп – у навколишньому середовищі біля поверхні кристала, дC/дn – градієнт концентрації по напря-
94
му нормалі до поверхні. Цю умову виражає рівність потоку речовини, що підводиться дифузією, і кількості речовини, що входить в кристал при переміщенні міжфазної межі. Для розв’язку задачі зростання потрібно ще знати закон залежності швидкості росту від пересичення розчину Cп–Се (Се – рівноважна концентрація розчину) на фронті кристалізації. Якщо ця залежність нелінійна (як правило, це так), аналітичні вирішення проблеми взагалі не можна отримати.
Точніша умова балансу речовини в порівнянні з (3.49) повинна враховувати також дифузійний потік на межу з об’єму кристала. Проте при розгляді задач росту кристалів, як правило, обмежуються умовою (3.49). У разі зростання сферичних кристалів із слабких розчинів іноді замість рівняння дифузії (3.7) розглядають рівняння Лап-
ласа Ñ2C=0. Проте для інших форм кристала отримувані функції не приводять до узгодження з граничними умовами.
Найповніше аналітична теорія дифузійного зростання розроблена в роботах Любова із співробітниками [7]. Як випливає з [7], точний розв’язок нестаціонарної задачі дифузії у разі сферичної симетрії (мабуть, і для циліндрової) може бути знайдений шляхом ряду послідовних наближень з розгляду інтегрально-диференціальних рівнянь, що враховують загальний баланс речовини. Розв’язки, отримані по методу Іванцова [8], (див. нижче) для випадку постійної концентрації на межі розділу фаз, мають ту особливість, що для них добуток радіусу кристала на градієнт концентрації у його поверхні
r(дC/дn)ρ=Const, а відповідно радіус частинки виявляється пропорційний кореню квадратному від часу r~Öt.
3.3.5. Ріст циліндра і кулі з розчину при постійній поверхневій концентрації
Розглянемо випадок зростання з розчину сферичного кристала. Аналітичний розв’язок такої задачі отриманий Іванцовим [8] для
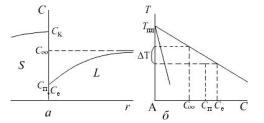
випадку постійної поверхневої концентрації (насправді при вільному зростанні кристала вона не буває постійною). Розподіл концентрації в рідині для випадку, коли ріст кристала визначається як поверхневими процесами приєднання атомів, так і дифузією у рідкому розчині, показано на рис. 3.3. Для опису росту кристала, у такому випадку, треба розглядати залежне від часу рівняння дифузії
¶C |
|
¶ |
¶C |
|
|
|
¶t |
= |
|
D |
|
або (дC/дt)=D(д2C/дx2) |
(3.50) |
|
||||||
|
¶x |
¶x |
|
|
||
|
|
|
|
|
|
95 |
(друге рівняння, якщо знехтувати залежністю коефіцієнта дифузії від концентрації), за крайових умов, що враховують початковий розподіл концентрації і умову балансу речовини на межі розділу фаз:
V(Cк – Сп) = D (дC/дn). |
(3.51) |
Розв’язок дифузійної задачі за порівняно складних граничних умов стикається з великими математичними труднощами. Тому аналітичні рішення отримані лише для тіл (кристалів) простої форми: сфер, циліндрів, параболоїдів обертання [8], а також простих тіл з невеликими спотвореннями їх форми [9], для випадків лінійної або квадратичної залежності швидкості росту від пересичення на фронті кристалізації.
Рис. 3.3. Розподіл концентрації під час росту кристала (а) та зв’язок
пересічення з переохолодженням бінарного розплаву (б).
Для задач росту поліедрів або простих форм часто замість рівняння дифузії (3.50) розглядають рівняння Лапласа Ñ2С=0.
У випадку малих пересичень, коли виконується співвідношення
Sc =(С∞ – Cп)/(Ск – Cп) << 1 для росту з розчину або Sт= сv (Tпл – T∞)/Lv << 1 (сv – питома, на одиницю об'єму, теплоємність, Lv – прихована теплота плавлення) для росту з розплаву, рівняння Лапласа дає правильні розподіли концентрації або температури поблизу поверхні зростаючої сфери за умови постійності їх значень на межі розділу фаз.
Знайдемо розв’язок рівняння Лапласа для випадку росту сферичної частинки з пересиченого розчину при умові постійної концентрації на її поверхні Cn=Ce (Cе рівноважна концентрація для певної постійної температури):
¶c |
|
¶2c |
|
2 ¶c |
|
¶2c |
|
2 ¶c |
|
|
||
|
= D |
|
+ |
|
|
|
+ |
|
|
= 0 . |
(3.52) |
|
¶t |
|
¶r2 |
|
r ¶r |
|
¶r2 |
|
r ¶r |
|
|
||
96

З умови балансу речовини на міжфазній межі (3.51)
|
∂C |
V(Cк − Сп ) = |
. |
|
∂r R |
Взагалі, швидкість визначається |
поверхневим пересиченням |
σп = μп /kT = (Cп − Ce )/Ce , тобто значенням концентрації в середовищі біля поверхні кристала: V = f (σп ). Але при збільшенні розміру кристала Cп→Cе. На великих відстанях від кристала C→C∞.
В рівнянні Лапласа робимо заміну |
∂C = U : |
∂U + |
2 |
U = 0 . Розділяє- |
|
||||
мо змінні й інтегруємо рівняння |
∂r |
∂r r |
||
|
|
|
|
|
∫dUU = −∫ 2rdr lnU = −2 lnr + ln A; U=A/r2.
∫dc = ∫ A ; C = − A + B . dr r2 r
Знаходимо сталу В з граничної умови на нескінченності:
r = ∞ B = C∞ , а сталу А з умови, що на міжфазній межі концентра- |
||
ція рівноважна: Cп=Cе (ріст лімітується дифузією). |
|
|
r = Rкрист C = Ce Ce = − A + C∞ |
|
|
R |
C = C∞ − C∞ − Ce R . |
|
A = (C∞ − Ce )R ; |
(3.53) |
|
|
r |
|
З умови балансу речовини визначаємо швидкість росту в чисто дифузійному режимі
V = D |
1 |
(C∞ − Ce ) |
, |
(3.54) |
|
||||
|
r (CK − Ce ) |
|
|
|
C∞ – початкова концентрація розчину.
Розв’язок рівняння дифузії (3.50) для росту сфери при постійній поверхневій концентрації, знайдене Р.П. Іванцовим, має вигляд
|
ρ exp(− |
λ2 r2 |
) − λ |
|
|
erfc( |
λr ) |
|
|
|
|
π |
|
||||||
C − C∞ = (Cď − C∞ ) |
r |
ρ2 |
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
, |
(3.55) |
|
|
2 |
|
|
|
|
|
|||
|
− λ |
|
|
|
|||||
|
exp(−λ ) |
π erfc(λ) |
|
||||||
де врахована гранична умова С=С∞ при r = ∞. На основі цього розв’язку з (3.13) можна знайти залежність розміру кристала від ча-
су: r =2 λ 
 Dt , причому λ визначається рівнянням
Dt , причому λ визначається рівнянням
2λ2 [1 − 2 |
π |
exp(λ2 )erfc(λ)] = Sc . |
(3.56) |
97

При Sc=(С∞ – Cп)/(Ск – Cп) << 1 (3.56) зводится до рівності λ = 
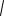 Sc /2 .
Sc /2 .
Якщо тепер в (3.55) знехтувати членом порядку λ порівняно з членом порядку 1 (λ << 1) і також вважати, що λr/ρ<<1, то С – C∞ =(Сп –
C∞) ρ/r. Тобто в цьому випадку поблизу від кристала розподіл концентрації збігається з розв’язком рівняння Лапласа (3.53).
3.3.6. Про тепло- і масоперенесення при вирощуванні монокристалів
Це питання висвітлене в книзі [1]. Найширше при вирощуванні монокристалів застосовується метод Чохральського. У процесі витягування монокристала тигель і зростаючий монокристал обертаються з певними швидкостями, причому, монокристал здійснює ще вертикальну поступальну ходу. Після розплавлення навантаженого в тигель матеріалу і переходу в стаціонарний режим теплота, отримана нагрівачем, витрачається на компенсацію різного роду втрат: (охолоджування струмовводів, променистий теплообмін кристала і нагрівача з охолоджуваними стінками камери і тому подібне).
Проблему теплообміну при вирощуванні монокристалів методом Чохральського розглядають в циліндровій системі координат r, ϕ, z. Сумістимо вісь z з монокристалом. Позначимо радіальну складову швидкості руху розплаву через wr, азимутальну – через wϕ і осьову складову через wz. Вважатимемо, що рух розплаву має осьову симетрію, тобто похідні від складових швидкості руху розплаву по коор-
динаті ϕ рівні нулю. Допустимо, що щільність розплаву є постійною величиною. В процесі роботи печі в розплаві встановлюються неста-
ціонарні поля швидкостей руху розплаву wr, wϕ і wz, тиску Р, а також температури розплаву Т і парціальної густини домішок.
Тепловий стан розплаву може бути описаний диференціальними рівняннями:
а) нерозривності
|
|
|
|
|
|
|
|
|
1 ∂ρ |
|
∂wr |
|
|
wr |
|
|
∂wz |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
+ |
|
|
∂r |
+ |
|
|
+ |
∂z = 0 ; |
|
(3.57) |
||||
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
r |
|
|||||||||||||
|
∂wr |
+ w |
|
∂wr |
|
− |
wϕ2 |
|
+ w |
|
∂wr |
= − |
1 |
∂P + g |
|
+ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
б) руху |
∂t |
|
r ∂r |
|
|
|
|
|
r |
|
|
|
z |
|
∂z |
|
|
|
ρ ∂r |
r |
; (3.58) |
||||||
|
∂ 2 wr |
|
|
∂ |
wr |
|
|
|
∂ 2 wr |
|
|
|
|
|
|
|
|||||||||||
|
η |
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
||||
|
∂r |
2 |
|
∂r |
|
∂z |
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
98
|
∂wϕ |
|
+ wr |
∂wϕ |
+ |
wr wϕ |
|
|
|
|
∂wϕ |
|
|
|
|
|
∂ 2 wϕ |
+ |
|
|
∂ wϕ |
+ |
∂ 2 wϕ |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ wz |
|
|
|
|
= η |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
||||||
|
∂t |
|
|
|
∂r |
|
|
|
|
r |
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
∂r r |
|
|
||||||||||||||||||
∂w |
|
|
|
∂w |
|
|
|
|
|
∂w |
|
|
|
|
1 ∂P |
|
|
|
|
∂ 2 w |
|
|
|
1 |
|
|
∂w |
|
|
|
∂ 2 w |
|
|
|
|||||||||||||||
|
|
z |
+ wr |
|
|
z |
+ wz |
|
|
z |
= − |
|
|
|
|
+ η |
|
|
|
2 z |
+ |
|
|
|
|
|
|
z |
+ |
|
|
2 z |
+ gz ; |
||||||||||||||||
|
∂t |
|
|
∂r |
|
∂z |
ρ ∂z |
∂r |
r |
|
|
|
∂r |
|
∂z |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
в) температурного поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
∂T |
+ wr |
∂T |
+ wz |
∂T |
= α |
T |
|
∂2T |
+ |
1 ∂T |
+ |
∂ 2T |
|
; |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
(3.59) |
||||||||||||||||
|
|
|
|
|
|
∂t |
|
∂r |
∂z |
|
∂r |
|
r ∂r |
∂z |
|
|
|
||||||||||||||||||||||||||||||||
г) дифузії |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∂C |
|
|
|
∂С |
|
|
|
|
∂С |
|
|
|
|
∂2С |
|
|
|
1 ∂С |
|
|
|
∂2С |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
∂t |
+ wr |
|
∂r |
+ wz |
∂z |
= D |
∂r2 |
|
|
+ |
|
|
|
∂r |
+ |
|
∂z2 |
. |
|
|
|
(3.60) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
В записаній системі рівнянь прийняті наступні позначення: η – коефіцієнт кінематичної в'язкості розплаву; Р – тиск розплаву; αТ – коефіцієнт температуропровідності розплаву;
D – коефіцієнт дифузії домішок в розплаві, С – їх концентрація. У систему з шести рівнянь входять 6 шуканих функцій: wr, wϕ, wz,
Р, Т, С. Для однозначності розв’язку повинні бути задані початкові поля у момент часу t=0 і граничні умови.
Крім того, необхідно знайти температурне поле в монокристалі, оскільки від нього залежать механічна напруга і утворення дефектів. Температурне поле монокристала також є нестаціонарним. Воно описується рівнянням
∂T |
∂T |
|
∂2T |
1 |
∂T |
∂2T |
|
cr + wz |
cr = αT |
cr + |
|
cr + |
cr . |
(3.61) |
|
|
|||||||
∂t |
∂z |
|
∂r2 |
r ∂r |
∂z2 |
|
|
Концентраційне поле у монокристалі також є нестаціонарним і визначається рівнянням
∂C |
|
∂C |
|
|
∂2C |
|
1 |
∂C |
|
∂2C |
|
|
|
cr + wz |
|
cr = Dcr |
|
cr + |
|
|
cr + |
|
cr . |
(3.62) |
|
|
|
|
|
|
|
|||||||
∂t |
∂z |
|
∂r2 |
r ∂r |
∂z2 |
|
||||||
Для фронту кристалізації справедливе рівняння теплового балансу
99
r |
|
|
|
|
|
h f |
r |
|
|
|
|
|
|
cr |
κ2πr |
dT |
dr+ |
|
κ2πr |
dT |
dz + (wcr + w)πr2ρ = |
||||||
∫ |
∫ |
||||||||||||
|
|
|
|||||||||||
0 |
|
dz |
0 |
|
|
dr |
|||||||
|
|
|
|
|
|
, (3.63) |
|||||||
|
|
|
|
|
|
|
|
||||||
rcr |
|
|
dTcr |
|
|
hfr |
|||||||
∫ |
κcr 2πr |
dr+ ∫ |
κcr 2πr |
dTcr |
dz |
||||||||
|
|
||||||||||||
0 |
|
|
dz |
|
0 |
|
|
|
dr |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
де hfr – положення фронту кристалізації; κ і κcr – відповідно коефіцієнти теплопровідності розплаву і кристала.
Поверхня розділу фаз визначається рівнянням Лапласа
1 |
+ |
1 |
= |
P |
, |
(3.64) |
|
|
|
σ |
|||||
R |
R |
2 |
|
|
|
||
1 |
|
|
|
|
|
|
|
де R1 і R2 – головні радіуси кривизни поверхні, σ – капілярна постійна.
Причини, що породжують рух розплаву, вельми різноманітні. Нерівномірне поле температур створює в розплаві неоднорідне поле щільності. Взаємодії гравітаційних сил з полем щільності розплаву приводить до появи течії, званої вільною конвекцією. Вільна конвекція виникає також за наявності відцентрових і коріолісових сил, які з'являються при обертальному русі розплаву. Течія розплаву може також породжуватися електромагнітними силами, різного роду механічними чинниками.
Рух розплаву в тиглі описується рівняннями нерозривності, збереження імпульсу, збереження енергії і граничними умовами. У більшості випадків отримати вирішення цих рівнянь не представляється можливим. Тому доводиться вводити різного роду передумови, що приводять до створення моделі досліджуваного процесу, яка відрізняється простішим математичним описом. За допомогою моделей вдається отримати ряд математичних залежностей, що представляють практичний інтерес [1]. Проте за достатньо складних граничних умов аналітичний розв’язок рівнянь стає неможливим і рівняння, що описують рухи розплаву, дифузію і теплопровідність, доводиться вирішувати чисельно. При складній формі фронту кристалізації потрібно вибирати дрібні сітки для апроксимації рішення сітковими функціями. Тому розрахунки можуть виявитися дуже тривалими, навіть при використанні найсучасніших комп'ютерів.
100
