
Ovru-all
.pdfУ чисельному аналізі обчисленням передує побудова фізичної теорії та виведення певних математичних співвідношень між фізичними величинами. Наприклад, ми знаємо, що розв’язання багатьох фізичних задач може бути зведене до розв’язання системи лінійних рівнянь. Аналітичний розв’язок можна знайти для системи з двох, трьох, чотирьох рівнянь. Якщо ж число змінних стає дуже великим, доводиться удаватися до чисельних методів і комп'ютерів. В даному випадку комп'ютер служить інструментом чисельного аналізу. Часто буває необхідно обчислити багатовимірний інтеграл, провести операції з великими матрицями або розв’язати складне диференційне рівняння. Це зумовлює широке застосування комп'ютерів у фізиці.
Усе більше значення набуває застосування комп'ютерів в теоре-
тичній фізиці для аналітичних (символьних) перетворень. Аналі-
тичні перетворення закладені вже в багатьох сучасних математичних пакетах, наприклад: Mathcad, Matlab, Maple, Mathematica. У якості прикладу припустимо, що ми хочемо дізнатися розв’язок квадратичного рівняння ах2 + bх + с = 0. Програма аналітичних перетворень може видати розв’язок у вигляді формули х = (-b ± (b2 – 4ac)½)/2a, або в звичайній числовій формі для конкретних значень а, b і с. Таким чином, комп'ютер може вже і виводити формули. Це особливо важливо, коли формули містять багато членів або коли для їх виводу потрібно багато операцій. Людина, швидше за все, помилиться, а комп'ютер дасть правильну відповідь.
За допомогою типової програми аналітичних перетворень можна виконувати такі математичні операції, як диференціювання, інтегрування, розв’язання рівнянь і розкладання в степеневий ряд.
Математичне моделювання характеризується тим, що в алгоритм закладаються тільки основні фізичні закони (принципи) з мінімальним аналізом. Як приклад припустимо, що потрібно знайти розподіл за енергіями в системі з багатьох частинок. Тобто відповісти на питання, яка ймовірність того, що значення енергії частинки знаходиться в інтервалі від Е до Е+ΔЕ. Один зі способів знайти відповідь на таке питання полягає в проведенні експерименту, наприклад, по визначенню швидкості руху молекул газу. Такі експерименти виконувалися. Але вони непрості, а дають відповідь на питання про розподіл саме молекул газу за енергіями. Дану задачу можна розв’язати точно аналітичними методами. І вона розв’язується в статистичній фізиці. Це задача про розподіл за енергіями частинок у системах, що входять у мікроканонічний ансамбль систем (таких, які складаються з великого числа частинок з постійною сумарною енергією). Проте,
11
не завжди подібні задачі розв’язуються аналітично. Набагато простіше вчинити інакше, а саме закласти правила гри для обмінів енергією між частинками в програму для комп'ютера, змоделювати велике число обмінів і обчислити ймовірності для знаходження розподілу. Комп'ютер можна також використовувати для з'ясування питань типу «Що буде, якщо...?» Наприклад, як би змінився розподіл частинок за енергіями, якщо змінити максимально можливу порцію енергії для обміну? Що буде, якщо обмін проводитиметься дискретними порціями енергії? Вказаний тип моделювання може знаходити застосування в задачах упорядкування систем із багатьох частинок, магнетизму, поведінки діелектриків.
При всій різноманітності використання комп'ютерів головною метою розрахунку є зазвичай «розуміння, а не числа». Комп’ютери дуже вплинули на характер занять фізикою, і на вибір фізичних систем для вивчення. Чисельний аналіз і моделювання вимагають аналізу проблеми, вибору моделі та спрощуючих наближень, що дозволяють розв’язати задачу чисельно. Проте, на перший план висувається саме творча робота дослідника.
Комп'ютери є також важливим інструментом в експериментальній фізиці – управління фізичним устаткуванням. Часто вони пов'язані з усіма фазами лабораторного експерименту, від проектування апаратури, управління цією апаратурою в ході експерименту і до збору й аналізу даних. Це залучення обчислювальної техніки не тільки дозволило експериментаторам краще спати ночами, але зробило можливим експерименти, які інакше були б нездійсненними. Деякі зі згаданих завдань, наприклад проектування апаратури або ж аналіз даних, близькі до завдань, що зустрічаються в теоретичному розрахунку. Проте завдання, пов'язані з управлінням і інтерактивним аналізом даних, якісно відрізняються і вимагають програмування в реальному часі і стиковки обчислювального устаткування з різноманітними типами пристроїв.
1.1.5.Обчислювальні експерименти та їхня роль
усучасній фізиці
Чому чисельне моделювання є важливим для фізики? Одна з причин полягає в тому, що більшість уживаних нами аналітичних засобів, таких як диференціальне числення, більш за все підходить для дослідження лінійних задач. Наприклад, легко аналізувати рух однієї частинки, підвішеної на пружинці, розв’язуючи рівняння її руху (другий закон Ньютона) в припущенні лінійної повертаючої сили. Проте безліч природних процесів є нелінійними, так що малий
12
приріст однієї змінної може привести до великих зрушень в значеннях інших змінних. Нелінійні задачі вдається розв’язувати аналітичними методами тільки в окремих випадках, а комп'ютер дає можливість дослідження нелінійних явищ. Інший напрямок чисельного моделювання – аналіз поведінки систем з багатьма ступенями вільності (що складаються з великого числа частинок) або багатьма змінними.
Розвиток комп'ютерної технології призводить до нового погляду на фізичні системи. Постановка питання: «Як можна сформулювати завдання для комп'ютера?» призвела до зміни формулювання деяких фізичних законів, до усвідомлення того, що цілком практично і природно виражати закони у вигляді правил для комп'ютера, а не мовою диференціальних рівнянь [1]. Зараз цей новий погляд на фізичні процеси приводить деяких фізиків до розгляду комп'ютера як якоїсь фізичної системи і розробки новітньої архітектури комп'ютерів, які можуть ефективніше моделювати природні фізичні системи. Часто чисельне моделювання називають обчислювальним експериментом, оскільки воно має чимало спільного з лабораторними експериментами. Деякі аналогії показані в табл. 1.1.
ТАБЛИЦЯ 1.1. Аналогії між обчислювальним і лабораторним експериментами
Лабораторний експеримент |
Обчислювальний експеримент |
Зразок |
Модель |
Фізичний прилад |
Програма для комп'ютера |
Калібрування |
Тестування програми |
Вимірювання |
Розрахунок |
Аналіз даних |
Аналіз даних |
Чисельний експеримент має ту перевагу, що в ньому умови, за яких протікає певний процес, задані точно. У реальному експерименті їх, як правило, дуже важко визначити.
Відправним пунктом чисельного моделювання є розробка моделі даної фізичної системи, що ідеалізується. Потім необхідно визначити процедуру або алгоритм для реалізації даної моделі на комп'ютері. Комп'ютерна програма моделює фізичну систему і описує обчислювальний експеримент. Такий обчислювальний експеримент слугує мостом між лабораторними експериментами і теоретичними розрахунками. Наприклад, ми можемо отримати по суті точні результати, для ідеалізованої моделі, у якої немає лабораторного аналога. Порівняння результатів моделювання з відповідними теоретичними розрахунками сприяє розвитку обчислювальних методів. З іншого боку,
13
можна проводити моделювання на реалістичній моделі з тим, щоб здійснити порівняння з лабораторними експериментами.
Вибір методу математичного моделювання для систем з великою кількістю частинок, залежить не тільки від бажання дослідника. При виборі методу моделювання головним є: розмір і оточення фізичної системи (кількість частинок, які утворюють певний фізичний континуум з певними граничними і зовнішніми умовами), точність розрахунку і можливість з певною достовірністю інтерпретувати отримані результати; тривалість обчислювального експерименту. Для кожного конкретного випадку необхідно вносити певні корективи, обирати деякі кореляційні коефіцієнти, враховувати характер взаємодії частинок, оцінювати похибки. В будь-якому випадку треба проводити низку тестових обчислювальних експериментів із заздалегідь відомими результатами. І лише за умови отримання позитивних результатів можна стверджувати, що створена нами математична модель, реалізована у комп'ютерну програму, є дієвою і можливою для використання і прогнозування фізичних властивостей системи.
Чисельне моделювання, як і лабораторні експерименти, не замінює роздум, а є інструментом, який можна використовувати для збагнення складних явищ. Але мета всіх наших досліджень фундаментальних фізичних явищ полягає в пошуку таких їх пояснень, які можна «записати на оборотному боці конверта», або які можна «представити на пальцях» [1].
1.2. Знаходження статистичних характеристик систем за методом Монте-Карло
1.2.1. Проблема пошуку рівноважних станів і середніх значень фізичних величин
Статистична фізика зазвичай має справу з системами, що складаються з величезної кількості частинок. Статистичний опис таких систем, в принципі, давно був розроблений в працях Максвелла, Больцмана, Гіббса. Цей опис має імовірнісний характер. Імовірність здійснення конкретної конфігурації усіх ступенів вільності у стані термодинамічної рівноваги системи визначається законами механіки (класичної або квантової), які керують еволюцією системи в часі. Ступенями вільності можна вважати набір незалежних фізичних величин механічної системи (наприклад, тривимірних координат частинок ri= (xi, уi, zi), де i=1,..., N (для газу з N точкових частинок),
14
який визначає її конфігурацію в даний момент часу. Значення всіх ступенів вільностей визначають мікростан системи (конкретну її конфігурацію), будемо позначати його літерою s. Відповідно до основного постулату статистичної фізики, всі мікростани макроскопічної системи з постійною енергією та кількістю частинок (а їх величезна кількість, Wо) рівноймовірні. Тому ймовірність реалізації конкретного мікростану s є дуже малою, ps=1/Wо. Імовірність макростану m, який визначається макроскопічними параметрами (P, T, V та ін.), для такої системи pm=Wm/Wо, де статистична вага Wm – це кількість мікростанів, що відповідають макростану m.
Статистична фізика вказує на те, як можна обчислювати розподіли ймовірностей станів різних систем (наприклад, таких, що контактують з термостатом – дуже великим тілом). Ці розподіли можна використовувати для обчислення фізичних величин. Втім, за винятком деяких простих випадків, таких, як ідеальний газ невзаємодіючих частинок або система лінійно-взаємодіючих гармонічних осциляторів (наприклад, маятників, зв’язаних пружинками), обчислення фізичних величин пов’язано з великими математичними труднощами.
Скажімо, для газу з n взаємодіючих частинок, що мають координати ri , i=1,..., n, нормована функція розподілу ймовірностей f(r1,..., rn) залежить від усіх цих змінних та, в принципі, відома в кожному окремому випадку. Позначимо A(r1, ..., rn) деяку фізичну величину, яка становить собою також конкретну довільну функцію змінних ri. Тоді середнє значення <A> , що нас цікавить, для стану термодинамічної рівноваги являє собою наступний багатократний інтеграл:
∞ |
∞ |
∞ |
|
<A> = ∫ dr1 |
∫ dr2 … ∫ drn A(r1, ..., rn) f(r1, ..., rn). |
(1.1) |
|
-∞ |
-∞ |
-∞ |
|
Задача обчислення такого інтеграла у випадку великих n або для n→∞ є винятково складною.
Часто зустрічаються ситуації, коли змінні ступені вільності, приймають дискретний набір значень. Тоді замість багатократних інтегралів треба обчислювати багатократні суми. Це також практично неможливо для систем з багатьма частинками. В якості приклада наведемо одну з найпростіших з точки зору формулювання і найбільш добре досліджених моделей статистичної фізики – феромагнетик Ізінга.
15
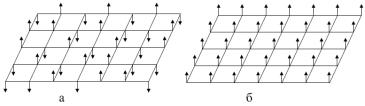
Як відомо, в реальному феромагнетику існують області переважно однакової орієнтації елементарних «магнітів». Така область зветься доменом. Орієнтація магнітних моментів різних доменів може бути різною, в результаті чого середній магнітний момент великої (макроскопічної) системи, у відсутності зовнішнього магнітного поля дорівнює нулю.
Рис. 1.1. Двовимірна модель феромагнетику Ізінга:
а– довільна конфігурація спінів;
б– конфігурація спінів з мінімальною енергією.
Феромагнетик Ізінга становить собою вкрай спрощену модель реального феромагнетику. Для її двовимірного варіанта Онсагером знайдено точний розв’язок задачі визначення рівноважних станів. Уявимо собі двовимірну квадратну гратку, в кожному вузлі якої розташований елементарний магнітний момент – спін, який може мати лише два виділених напрямки (рис. 1.1). Ізінгові спіни на цьому рисунку зображені стрілками, які спрямовані вгору або вниз. В даному випадку кожний спін становить окрему степінь вільності, причому відповідна їй змінна qi приймає лише два значення: qi=1 відповідає спінові, спрямованому вгору, а qi= –1 спінові, спрямованому вниз. Найближчі один до одного спіни qi і qj, взаємодіють між собою, причому енергія Еij взаємодії може бути представлена у вигляді
Еij= –Jqiqj, |
(1.2) |
якщо i-й та j-й сусідні спіни спрямовані в один і той самий бік, Еij =– J, а в разі протилежної спрямованості Еij =J. У відповідності до законів статистичної механіки, у стані термодинамічної рівноваги дана конфігурація усіх спінів системи, яка характеризується набором значень змінних qi, здійснюється з імовірністю, що задається функцією розподілу Гіббса (канонічний розподіл для систем, що контактують з термостатом):
f (q1 |
,...,qn ) = |
1 |
|
1 |
|
exp − |
|||||
Z |
kT |
||||
|
|
|
|||
|
|
|
|
|
∑ Eij , (1.3)
за зв'язками(i, j)
16
де Т – абсолютна температура за Кельвіном; k — стала Больцмана; Z – множник нормування, який зазвичай зветься статистичною сумою, він визначається з умови
|
∑ ∑ ××× ∑ W (q1 ,...,qn ) =1 , |
|
(1.4) |
|||
q1 =±1 q2 =±1 qn =±1 |
|
|
|
|
||
тобто |
|
|
|
|
|
|
|
|
1 |
|
|
||
Z = ∑ ∑ |
××× ∑ |
exp - |
|
∑ |
Eij . |
(1.5) |
|
||||||
q1=±1 q2 =±1 |
qn =±1 |
|
kT за зв'язками (i, j) |
|
|
|
Припустимо тепер, що ми хочемо обчислити, наприклад, середню енергію <E> за температури Т. Енергія даної конфігурації спінів дорівнює
Es(q1 ,...,qn ) = |
∑ |
Eij = -J |
∑ |
qiqj . |
(1.6) |
|
за зв′язками (i,j) |
|
за зв′язками (i,j) |
|
|
Середня енергія <Е> (як, втім, і середнє від будь-якої іншої фізичної величини) може бути знайдена за формулою:
 E
E = ∑ ××× ∑ E(q1 ,...,qn ) f (q1 ,...,qn ) =
= ∑ ××× ∑ E(q1 ,...,qn ) f (q1 ,...,qn ) =
q1 =±1 qn =±1
= |
1 |
∑ |
××× |
∑ |
|
- J |
∑ |
|
|
||||||
|
|
|
|
|
|
|
|
|
Z q1 =±1 |
|
qn =±1 |
|
за зв′язками |
||
|
|
|
|
|
´ |
|
qiq j |
|
(i,j) |
|
|
|
1 |
∑ |
|
. (1.7) |
exp |
|
qiq j |
|
|
|
|
|||
kT за зв′язками(i, j) |
|
|
||
Оскільки кожна спінова змінна qi може приймати два значення, простір конфігурації системи з n спінів (його зазвичай називають фазовим простором) складається з 2n можливих конфігурацій. В принципі, при будь-якому кінцевому n суму (1.7) можна обчислити точно. Однак для вивчення властивостей макроскопічної системи число спінів треба брати великим. Наприклад, у разі моделі Ізінга число спінів має бути принаймні порядку 102 для того, щоб результати обчислення середньої енергії та інших фізичних величин були близькими до їхніх значень в системі з нескінченним числом спінів.
Здавалося б, обчислення суми вигляду (1.7) треба одразу ж доручити ЕОМ. Однак підсумовування 2100 членів ряду (1.7) – задача, недосяжна для будь-якої ЕОМ. Втім, з цього не випливає принципова неможливість аналізу статистичних моделей на комп’ютері.
З розгляду кількостей конфігурацій, що відповідають різним енергіям системи, стає зрозумілим, що внесок різних доданків в суму (1.7) зовсім не рівноцінний. Наприклад, конфігурація спінів, в якій будь-які два сусіда спрямовані в один бік, як це зображено на рис. 1.1,б, тільки одна. І, незважаючи на мінімальне значення енергії
17
системи, імовірність реалізації стану з такою енергією дуже мала. Існує дуже багато мікростанів, що відповідають високим енергіям, коли багато пар сусідніх спінів, направлених у різні боки. Але для таких конфігурацій дуже мале значення експоненти від сумарної енергії (від – Е/kТ), і за помірних температур вони не реалізуються. Але станів з меншою енергією теж дуже багато, і їхня кількість може компенсувати мале значення експоненти. Зазвичай в такому разі говорять, що стани системи в даній області енергій мають високу ентропію, яка може компенсувати малість усіх цих членів.
Під ентропією S(Е) станів з даною енергією Е треба розуміти логарифм числа W(Е) цих станів: S(Е)=log W(Е). Кожному енергетичному макростанові системи з енергією Е відповідає W(Е) мікростанів. Тому ймовірність конфігурації, тобто ймовірність потрапити у певний мікростан з конкретним набором координат (ступенів вільності) та сумарною енергією Е,
f(E)~ W (E)ехр[–E/(kT)]=ехр[S(E) –E/(kT)]. |
(1.8) |
Ці ентропійно-енергетичні міркування мають обов’язково враховуватись у кожній скільки-небудь ефективній обчислювальній схемі. Саме такий принцип вибору конфігурацій за мірою важливості використовується у більшості сучасних алгоритмів для метода МонтеКарло – в алгоритмі Метрополіса, в алгоритмі термостата, і алгоритмі Кройца для ізольованої системи.
1.2.2. Основи методу Монте-Карло у застосуванні до фізичних проблем
Методами Монте-Карло (МК) зазвичай називають такі методи, в яких розв’язок у принципі детермінованих задач замінюється наближеним розглядом, заснованим на введенні стохастичних елементів, послідовності яких дозволяють знаходити наближені розв’язки. Сутність методу МК у застосуванні до задач статистичної фізики обговорюється у великій кількості монографій та оглядових статей, наприклад [3-5].
Оскільки всі стани системи досяжні (стан s характеризується набором значень мікроскопічних параметрів частинок та макроскопічних, наприклад, об’єм системи), існують імовірності переходу з одного стану в інший p(s→s’). Прийнято вважати, що сукупність усіх можливих станів s утворює ланцюг Маркова з постійними ймовірностями переходів зі стану s у стан s' ≥0, що задовольняють умові нор-
18
мування для усіх s, включно s=s': |
|
∑ p(s → s') = 1 . |
(1.9) |
s'
Згідно з теорією однорідних ланцюгів Маркова [6,7], перехід зі стану s у стан s’ за n кроків може здійснитись через різні проміжні стани. Позначимо через p(n)(s→s’) сумарну імовірність реалізації такого переходу усіма можливими шляхами із n кроків, а p(s→s’) – сумарну ймовірність переходу будь-яким шляхом. Якщо всі s стани утворюють один ергодичний клас, тобто з будь-якого стану s стан s’ є досяжним за деяке кінцеве число переходів, то існують граничні імовірності
p(S ′) = lim p(n) (S → S ′) , |
(1.10) |
n→∞ |
|
для усіх s і s’ незалежно від s. При цьому p(s’)≥0, ∑ p(S ′) = 1 . Рів-
s′
ність (1.10) означає, що перехід системи до стаціонарного розподілу станів не залежить від вибору початкового стану. В теорії ланцюгів
Маркова доводиться, що величини p(s’) пов’язані з p(s→s’) системою лінійних рівнянь
p(S ') = ∑ p(S )p(S → S ') , для усіх s’. |
(1.11) |
S |
|
Для методу МК, навпаки, p(s’) – відома, а p(s→s’) – шукана. Рівняння (1.9) і (1.11) можна розглядати як систему рівнянь відносно невідомих p(s→s’). В цій системі кількість невідомих перевищує кількість рівнянь, тому обрати p(s→s’) можна у різні способи. У просторі станів s існує велика кількість ланцюгів Маркова, що реалізують переходи s→s’. Конкретний вибір p(s→s’) здійснюється з міркувань простоти, а також виходячи з того, яка послідовність проміжних станів (який з можливих ланцюгів Маркова) швидше виходить на стаціонарну ділянку, і т. ін. Співвідношення
p(S )p(S → S ') = p(S ')p(S '→ S ) для усіх s і s’, |
(1.12) |
яке є виразом принципу мікроскопічної зворотності в системі або детальної рівноваги, перетворює (1.11), з урахуванням (1.9), на тотожність. Тому на практиці при побудові ланцюгів Маркова можна виходити з системи рівнянь (1.9) і (1.11). Оскільки (1.11) і (1.12) однорідні відносно p(s), для визначення p(s→s’) досить знати розподіл
p(s) з точністю до постійного множника. Явний вигляд p(s→s’) залежить від того, що розуміється під станом s. За допомогою відомих
19
p(s→s’), відповідна послідовність реалізується на ЕОМ наступним чином. Обирається деякий довільний стан s як початковий, потім випадковим чином обирається стан s’ зі станів, імовірність переходу до яких p(s→s’)≠0, і обчислюється ця імовірність. Знаючи значення p(s→s’), проводять випробування щодо того, чи здійсниться перехід s→s’, виходячи із принципу вибору конфігурацій за мірою важли-
вості. Такий вибір забезпечується при застосуванні більшості сучасних алгоритмів, що реалізують метод МК: Метрополіса, термостата, алгоритму Кройца для ізольованої системи. В послідовностях, які реалізуються під час моделювання, деякі стани можуть повторюватись (переважно, за рахунок переходів, що не здійснились). Втім, значна більшість станів s з усієї їхньої можливої сукупності взагалі не зустрічається. Незважаючи на це, послідовності виявляються досить репрезентативними. Обчислення з їх використанням призводить до точності обчислення середніх значень порядку 1 % або навіть краще. Саме мала кількість членів послідовності проміжних станів у порівнянні з загальною кількістю можливих станів s обумовлює суттєву перевагу вибірки за методом МК у порівнянні з іншими чисельними методами.
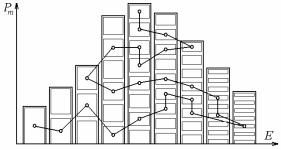
Рис. 1.2. Схематичне зображення розподілу конфігурацій системи за
енергіями.
Рис. 1.2 наочно демонструє принцип вибору станів (конфігурацій). На ньому схематично зображена діаграма станів деякої системи, згрупованих за енергіями, яка визначає сумарні ймовірності потрапляння системи у стани з певною енергією (діаграма функції Pm(Е)). Кожному прямокутникові відповідає певний стан (конфігурація). Висота прямокутників тим більше, чим менше енергія стану (вона пропорційна ехр[–E/(kT)] – це больцманівська імовірність потрапляння системи, що контактує з термостатом, в один зі станів з енергією E); число прямокутників в даному стовпчику відповідає
20
