
Ovru-all
.pdf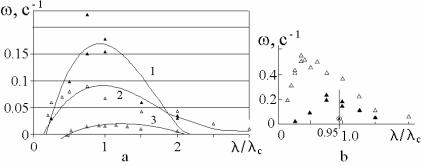
На рис. 6.27 показані послідовні профілі фронту кристалізації при введені у початкові умови невеличких періодичних збурень поверхні.
Оскільки швидкість розвитку збурень (зростання амплітуди комірок) збільшується з часом, то її зручно характеризувати експонен-
ціальною складовою ω залежності амплітуди від часу:
ξ(r,t)=ξ0+ξkexp(ikr)exp(ωt),
де k – хвильовий вектор, |k|=2π/λ.
Рис. 6.28. Залежності швидкості розвитку збурень від їхньої довжини хвилі: a) (2D), lc=1.68×10-4 м: 1 – ν=3, zγ=0, zβ=0.4, β=0.15 м/с; 2 – ν =3, zβ=0,
zγ=0.06, β =0.5 м/с; 3 – ν =1.5, zβ=0, zγ=0.06, β=0.5 м/с. b) β=0.15 м/с, zγ=0, lc=1.68×10-4 м, l0 teor=1.38×10-5 м: 3D: D – ν=3, zβ=0.4; 2D: ▲ – ν=3, zβ=0.4.
В [52] встановлено, що збурення розвиваються в певних діапазонах довжин хвиль. На кривих залежності ω(λ) є максимум, який зміщується вбік менших довжин хвиль зі збільшенням ν (рис. 6.28). Для
порівняно низького значення ν (=1.5) (рис. 6.28, a, крива 3) дані моделювання мало відрізняються від значень, розрахованих згідно з теорією Маллінза і Секерки. При більшій швидкості протягування
(ν=3, рис. 6.28, a, криві 1, 2) швидкості розвитку збурень вже суттєво перевищують теоретичні значення. Це цілком зрозуміло, оскільки зазначена теорія розроблена тільки для випадку дуже малих амплітуд збурень.
У двовимірному (ізотропному) випадку максимум залежності
ω(λ) припадає на значення λ 0.9λс 1.6λ0 5.8λ0 theor при ν=1.5 (значення λ0 визначались з графіків, подібних до зображених на рис. 6.28), і
λ 0.55λс 3.5λ0 6.7 λ0 theor при ν=3. В тривимірному випадку максимум
201

припадає на значення λ @ 0.5λс @ 1.8λ0 @ 3.6 λ0-theor при n=1.5, і
λ @ 0.4λс @ 3.1λ0 @ 5.0×λ0-theor при n=3.
Знайдені значення λ0 – мінімальної довжини хвилі, яка може розвиватись у двовимірному випадку, (λ0= 0.56λс при n=1.5 і λ0= 0.16λс
при n=3) у 2-3 рази перевищують значення λ0-theor (2.76×10-5м і 1.38×10 –5 м, відповідно). У тривимірному випадку, отримані при мо-
делюванні значення λ0 (λ0 = 0.28λс при n=1.5 і λ0 = 0.13λс при n=3), перевищують результати теорії малих збурень в 1.5-2 рази.
На рис. 6.28, b відображені швидкості розвитку збурень при ані-
зотропному кінетичному коефіцієнті. Маркером 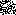 позначено граничне значення довжин хвиль, за яких відбуваються біфуркації у двовимірному випадку, для залежності, позначеної маркерами ▲. Наведені значення отримані для двох орієнтацій кристала (двовимір-
позначено граничне значення довжин хвиль, за яких відбуваються біфуркації у двовимірному випадку, для залежності, позначеної маркерами ▲. Наведені значення отримані для двох орієнтацій кристала (двовимір-
ний і тривимірний випадок, n=3). При максимумі кінетичного коефіцієнта в напрямку протягування збурення розвиваються швидше.
Як можна бачити з рис. 6.28, a, анізотропія кінетичного коефіцієнта (крива 1) та поверхневого натягу (крива 2) по-різному впливають
на залежності w(l).
Автори [91] вивчали розвиток комірчастої структури при різних початкових збуреннях поверхні за методом фазового поля в дифузійному режимі (нескінченний кінетичний коефіцієнт). При цьому обмежувались випадком суто дифузійного росту (рівноважна концентрація на поверхні кристала) та слабкої анізотропії поверхневої енергії (1 %). При накладенні початкового збурення, що задається двома хвильовими функціями різних амплітуд, автори отримували досить специфічні форми комірок.
Рис. 6.29. Розвиток комірчастої структури при різнохвильовому почат-
ковому збуренні в розплаві системи сукцинонітрил-кумарин,
ν=5, анізотропія zγ=0.01 [91].
202
Розділ 7.
КОМП’ЮТЕРНІ МОДЕЛІ АТОМНИХ ПОВЕРХНЕВИХ ПРОЦЕСІВ
7.1. Пошук рівноважних структур за методом Монте-Карло та їх аналіз
7.1.1. Пошук рівноважних структур
Для визначення геометричної будови речовини (конфігурації атомів) зазвичай використовують алгоритм релаксації, який полягає в мінімізації потенціальної енергії. При цьому потенціали міжчастинкової взаємодії мають бути відомими. Для системи задають довільну початкову конфігурацію i внаслідок дії алгоритму знаходять структуру, яка відповідає мінімуму енергії. При релаксації за методом спуску виконується мінімізація потенціальної енергії U(r1, r2…,rN) як функції багатьох змінних (координат атомів). Почат-
кові значення координат r10, r20…,rN 0 обираються довільно. Пошук мінімуму функції U (r1, r2…,rN) здійснюється почергово уздовж кожної з осей. Для цього порівнюються значення функцій U(r1+dr1, r2…,rN) і U(r1–dr1, r2…,rN) та обирається той напрямок зсуву +dr1 або – dr1, в якому значення потенціальної енергії зменшується. Так само уздовж інших осей. Далі процес пошуку локального мінімуму повторюється доти, доки не буде досягнута дуже мала зміна потенціальної енергії за один крок ітерації. Якщо в обох напрямках
±dri значення U(r1, r2…,rN) зростає, то це означає, що мінімум знахо-
диться ближче, ніж ±dr, отже, необхідно зменшити крок dri.
Пошук можна також здійснювати не почергово уздовж кожної з осей, а обираючи нове місцеположення j-ї частинки після зсуву та-
R |
R |
V |
, де d – |
амплі- |
ким, що визначається формулою: rj |
= rj |
+ random ×d × r1 |
||
туда, r1 – довільний випадковий одиничний вектор. |
|
|
||
Існує модифікація цього методу – |
метод найшвидшого (градієнт- |
|||
ного) спуску. Оскільки відомо, що напрямок градієнту є напрямком найшвидшого зростання функції, то, зрозуміло, що протилежний напрямок є напрямком найшвидшого спадання. Таким чином, пошук мінімуму при застосуванні методу найшвидшого спуску здійснюється в напрямку антиградієнта, тобто в напрямку –ÑiU(r1, r2…,rN)=Fi. У рамках лінійного наближення, для одного з компонентів повної
сили Fx, що діє на і-й атом з боку усіх інших в межах сфери обрізання потенціалу, можна записати вираз:
203
Fx (ri + dri ) = Fx (ri )+ ∑ |
∂Fx (ri )drji . |
(7.1) |
j |
∂rji |
|
Для того щоб атом посів положення, що відповідає локальному мінімуму енергії, покладають Fx (ri+dri)=0, а для знаходження dri розв’язують систему N (трьох) лінійних рівнянь. Звісно, що зсув атома має чинити вплив на всі оточуючі його атоми. Однак при багаторазовому повторі цього процесу розрахунок за релаксаційною процедурою має збігатись, тобто зсув атомів має стати менше деякого попередньо заданого значення.
На відміну від методу спуску, при здійсненні релаксації з використанням методу Монте-Карло, нова конфігурація обирається випадково (генерується).
Алгоритм релаксації за МК методом складається з наступних кроків [1]:
1.Завдання початкової конфігурації.
2.Генерація нової конфігурації.
3.Обчислення зміни енергії δЕ.
4.Прийняття нової конфігурації у разі виконання умови δЕ <0 i виконання додаткових кроків, якщо ця умова не виконується:
а) обчислення ехр[– δЕ/kBT];
б) генерація випадкового числа Rand [0;l];
в) прийняття нової конфігурації у разі Rand < ехр[–δЕ/kBТ], інакше – повернення до кроку 2 без зміни конфігурації.
При роботі програми за цим алгоритмом система прямує до стану з мінімальною енергією, що відповідає сталим макроскопічним параметрам (N,V,T). Крок 4 передбачає, що нова конфігурація, з меншою, ніж попередня, енергією, завжди приймається. Конфігурації, що підвищують енергію системи, приймаються лише з Больцманівською ймовірністю (крок 4, в). Перехід до нової конфігурації реалізується за допомогою випадкових зсувів випадково обраних частинок.
204

7.1.2. Обчислення структурних характеристик
Першим моделювання за методом Монте-Карло системи твердих дисків виконав Метрополіс, пізніше Ротенберг провів моделювання для системи жорстких сфер, а Вуд – для потенціалу ЛеннардаДжонсона. Розглядалися N V T-ансамблі, аналізувалися визначені на
основі даних моделювання залежності p(V) [2].
Для аналізу структури змодельованих систем найчастіше розраховують наступні характеристики.
Парні функції радіального розподілу атомів g(r) (ПФРРА) характеризують імовірності певних відстаней між атомами (див. нижче).
Парціальні парні функції радіального розподілу gA-В(r) (ППФРРА) визначають радіальну залежність кількостей атомів типу В, які розташовані у сферичного прошарках на відстані r навколо атомів типу А:
|
1 |
M N |
|
|
gA-В(r) ~ |
∑∑ Pnm , |
(7.2) |
||
|
||||
|
MN m=1 n=1 |
|
||
де NA – кількість атомів сорту А; М – кількість незалежних конфігурацій, за якими розраховується дана функція, Рпт – кількість атомів сорту В навколо n-гo атому сорту А в m-ій незалежній конфігурації.
Середня конфігураційна потенціальна енергія:
M |
Em=(1/2) ∑ Ei, j , |
|
<E>=(1/M) ∑ Em , |
(7.3) |
|
m=1 |
i, j=1 |
|
де Ei,j – енергія ij-ї пари атомів у m-ій конфігурації. Трьохчастинкова кореляційна функція G(θ)
|
|
|
|
R |
R |
|
|
|
G(θ)= |
|
1 |
∑ |
ri, j rik |
|
, |
(7.4) |
|
|
|
R |
R |
| |
||||
N |
|
|||||||
|
|
| r |
| × | r |
|
|
|||
|
|
i, j ,k i, j ,k |
i, j |
i,k |
|
|
|
|
де Ni,j,k – число врахованих трійок атомів. Але частіше аналізують розподіли за кутами. Самі кути визначаються через компоненти ра- діус-векторів у напрямках на двох найближчих сусідів розглядувано-
го атома: (rijrik)=|rij||rik|cosθ.
7.1.3. Радіальна (парна) функція розподілу молекул
Розміщення атомів у кристалах описують за допомогою просторових граток. Але цей спосіб для рідин непридатний. У випадку рідин використовують функцію розподілу. Щоб скласти уявлення про функцію розподілу, розглянемо розміщення атомів у кристалі з по-
205
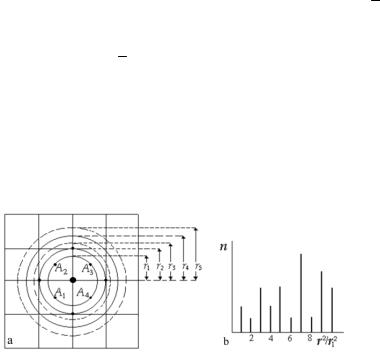
гляду оточення деякого обраного атома. Візьмемо в розгляд площину (100) гранецентрованої кубічної гратки. На рис. 7.1,а зображена плоска сітка, що відповідає даній кристалічній площині, відмічені деякі положення атомів та вказані характерні відстані між обраним атомом і тими, що його оточують.
Якщо обраний атом знаходиться в точці 0, яка є загальною вершиною для восьми елементарних комірок, то найближчі до нього атоми розміщуються в центрах граней сусідніх елементарних комірок (точки A1, A2, A3, A4) на однаковій відстані від даного атома. Опишемо коло радіусом r1, на цьому колі знайдемо 4 атоми. Якщо провести сферу радіусом r1 (так звану першу координаційну сферу),
то на ній буде n1=12 атомів. Проведемо ще коло радіусом r2= 
 2 .r1. На ньому також буде 4 атоми, а на сфері радіусом r2 (друга координаційна сфера) виявиться n2=6 атомів. Аналогічно для третьої коор-
2 .r1. На ньому також буде 4 атоми, а на сфері радіусом r2 (друга координаційна сфера) виявиться n2=6 атомів. Аналогічно для третьої коор-
динаційної сфери (r3= 
 3 ×r1) маємо n3=24, для четвертої (r4=2r1) – n4=12 і т.д. Ці результати відображені графічно на рис. 7.1,б. На осі абсцис відкладені значення відношення r 2/r12, а на осі ординат – відповідні їм числа атомів n. Такий графік називають графіком раді-
3 ×r1) маємо n3=24, для четвертої (r4=2r1) – n4=12 і т.д. Ці результати відображені графічно на рис. 7.1,б. На осі абсцис відкладені значення відношення r 2/r12, а на осі ординат – відповідні їм числа атомів n. Такий графік називають графіком раді-
ального розміщення атомів в ідеальному кристалі. У реальному кри-
сталі, в якому є різні дефекти, дальній порядок порушується тим сильніше, чим більшою є відстань від обраного атома. За відсутності дефектів розміщення атомів у кожний момент часу теж відрізняється від ідеального внаслідок теплових коливань атомів.
Рис.7.1. Схема взаємного розташування атомів (а) та графік раді-
ального розміщення атомів (б).
У випадку рідин та аморфних твердих тіл розглядають число атомів не на поверхні точно визначених сфер, а у сферичних прошарках. Якщо провести навколо даного атома дві сфери з радіусами r та
r+∆r, то об’єм сферичного шару буде дорівнювати 4pr2∆r. Визначимо функцію атомної радіальної густини через кількість атомів у такому шарі:
206

ρ(r) = |
nr |
, |
(7.5) |
4πr2 r |
тобто це середня кількість частинок в одиниці об’єму цього шару.
Позначимо через ρo середню густину атомів. Парною функцією радіального розподілу атомів (ПФРРА) називають відношення
g(r)=ρ(r)/ρo. (7.6)
Воно характеризує ймовірність появи атому в деякому шарі на певній відстані від довільно взятого атома. На рис. 7.2,а графічно зображена функція g(r) для рідкого натрію, яку одержали на основі рентгенівського дослідження. Ця функція спочатку зростає зі збільшенням r від значення g(r)=0 на малих відстанях, а потім змінюється так, що стає то більшою, то меншою за одиницю. Чим більша відстань від атома, який береться за початковий, тим менші відхилення значень функції g(r) від одиниці. З графіком радіального розподілу в ідеальному кристалі (рис. 7.1,б) краще порівнювати графік функції атомного розподілу 4πr2ρ(r), якісний вигляд якої відтворено на рис. 7.2,б. Добуток 4πr2ρ(r) ∆r визначає число атомів у сферичному шарі, утвореному сферами з радіусами r і r+∆r. Тому площі під піками графіка визначають кількості атомів у відповідних координаційних сферах. Площа під першим піком (вона заштрихована на рис. 7.2,б) визначає середнє число найближчих сусідніх атомів. Однак вирішення питання про те, як розділити між піками площу їх перетину, є досить складною проблемою. Тому з достатньою точністю можна визначити кількість атомів тільки для перших двох координаційних сфер. Пунктирна крива на рис. 7.2,б відповідає функції
4πr2ρо.
Рис. 7.2. Вигляд ПФРРА (а) та функції атомного розподілу (б).
Для побудови ПФРРА за даними моделювання треба просто просумувати кількості атомів у сферичних прошарках навколо кожного
207
із обраних послідовно атомів. Далі поділити середню кількість атомів у прошарку на об’єм цього прошарку й на середню густину.
Парна функція радіального розподілу атомів (ПФРРА) є фундаментальною характеристикою структури, як для однокомпонентних, так и для багатокомпонентних (парціальні ПФРРА) систем. У випадку однокомпонентних речовин розрахунок проводиться згідно зі співвідношенням:
g(r ) = |
ρ |
i |
= |
n(r , |
r)R3 |
|
|
i |
|
, |
|||
ρ0 |
|
|
||||
i |
|
N(r3 |
− r3 ) |
|||
|
|
|||||
|
|
|
|
i+1 |
i |
|
де N – число вимірів, які відповідають сфері радіусом R, n(ri, r) – число вимірів, які відповідають сферичному шару від ri до ri+1. Якщо в окремі масиві записувати дані про оточення кожного атому, можна побудувати ще розподіл атомів за числом оточуючих найближчих сусідів.
Наступне співвідношення дозволяє розраховувати парціальні ПФРРА
gij (r) = |
V nij (r) |
|
, |
N j 4πr2 |
|
||
|
r |
||
де nij(r) – число частинок сорту j, які знаходяться в сферичному шарі
rна відстані r від частинки сорту i; Nj/V – середня густина. Нижче показано лаконічний код (мовою С++) для підрахунку па-
рціальної ПФРРА (ukazatel[i] задає тип компонента 1 або 2):
for (int i = 0; i < COUNT; i++)
{ atom &a1 = a[i]; //перший атом if (ukazatel[i] ==1) NCOUNT++;
for (int j = 0; j < COUNT; j++) { if (j==i) continue;
if (ukazatel[j]==1) continue;
atom& |
a2 = a[j]; |
//інший атом |
double |
dr=(a1.r-a2.r).abs(); //відстань між атомами |
|
int nr = floor(dr*10);
if (nr>intR) continue; //intR– радіус сфери розрахунку g12[nr]++; //накопичення даних по шарам товщиною 0.1Å
} }
for (int ir = 0; ir < intR; i++) g12[i]=g12[i]/NCOUNT/(pow(ir+1,3)-pow(ir,3));,
208
де COUNT – кількість атомів, NCOUNT– кількість атомів першого ком-
понента, pow(ir,3))=ir*ir*ir, ir – номер прошарку.
Важливу інформацію можна отримати також з Фур’є перетворення ПФРРА, тобто зі структурного фактору системи. Такі дані дозволяють порівнювати отримані результати з експериментальними даними рентгеноструктурного аналізу та вивчати детальніше зміну структурних характеристик модельованих системи на атомарному рівні при термообробках. У роботі [5] результати моделювання термообробок аморфного заліза й сплаву системи Fe-B порівнювалися з експериментальними результатами, наведеними в [6].
Структурні характеристики модельованих об’єктів характеризуються набором просторових ізотропних та анізотропних кореляційних функцій. Однак характеристика структури у вигляді ПФРРА не дає повного уявлення про будову речовини. Подальшим кроком є побудова атомних моделей, що більш наглядно зображують просторове розташування частинок системи. Шляхи розв’язання цієї задачі широко розвинуті в кристалографії, але для некристалічних систем існує ряд труднощів, пов’язаних з недостатньою точністю вихідних даних і з можливою неоднозначністю розв’язку задачі. Тому застосовують алгоритми, що дозволяють побудувати атомну модель рідини або аморфної фази за дифракційними даними, наприклад обернений метод Монте-Карло.
7.1.4.Обчислення тиску та вивчення рівняння стану
Зтеореми про віріал сили випливає спосіб обчислення тиску. Розглянемо її виведення, наведене у книзі Хансена і МакДональда [7]. Запишемо величину суми від скалярних добутків
G = ∑ riFi , |
(7.7) |
i |
|
де сума береться за усіма частинками системи, а Fi є повна сила, що діє на i-ту частинку. Середнє за часом від G можна записати у вигляді
|
|
|
1 |
τ |
|
|
|
|
|
|||
G |
= lim |
∫ dt∑ ri(t)×Fi(t) = |
||||||||||
|
|
|
||||||||||
|
τ→∞ t |
0 |
i |
|
|
|
|
|||||
Враховуючи, що |
|
|
|
|
|
|
|
|
|
|||
|
d2r |
|
1 d2r2 |
dr |
2 |
|||||||
r |
|
= |
|
|
|
|
|
- |
|
|
|
|
dt2 |
2 |
|
dt2 |
|
|
|||||||
|
|
|
|
dt |
|
|||||||
|
|
1 τ |
|
|
|
|
|
|
d2r (t) |
|||||
lim |
|
|
∫ dt∑ri |
(t)× m |
i |
|
|
; |
||||||
|
|
dt |
2 |
|
||||||||||
τ→∞ t |
0 |
i |
|
|
|
|
|
|
|
|||||
|
mv2 |
|
= - |
rF |
|
+ |
1 |
m |
d2r2 |
, |
|
|||
2 |
|
|
2 |
|
|
|
||||||||
|
|
|
|
4 |
|
|
dt2 |
|
|
|
||||
209
(v – швидкість частинок), отримаємо після усереднення складових останньої рівності за часом:
mv2 |
|
1 |
τ |
mv2 |
|
rF |
|
1 |
|
d2r |
2 |
|
τ |
|
|
|
|
|
|
||||||||||
|
= |
|
∫ |
|
dt = - |
|
+ |
|
m |
|
|
|
|
. |
2 |
t |
2 |
2 |
4 |
dt2 |
|
||||||||
|
0 |
|
|
|
|
|
|
0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
У разі t®¥, d2 r2 ¹ ¥ , тому dt2
mv2 |
= - |
rF |
і G = -3NkBT , |
|
2 |
2 |
|||
|
|
де проведено інтегрування за частинами і використано теорему про рівнорозподіл. Вираз для G можна розбити на частини: одну, пов’язану із силами взаємодії частинок, і другу, зумовлену зовнішньою силою, що діє збоку стінок. Останню можна пов’язати з тиском і записати
dFi çîâí = −PndA , |
(7.8) |
де n – одиничний вектор нормалі до площинки dA. Тому
∑ ri dFi çîâí = -P∫ rndA = -P∫ divr dV = -3PV ,
i
де ми застосували теорему Гаусса і врахували, що div(r)=3. У результаті можна записати
- 3PV + Gint |
= -3NkBT . |
|
||||
Отже, |
|
|
|
|
||
P = |
NkBT |
+ |
1 |
|
∑ r × F , |
(7.9) |
|
|
|
||||
|
V |
3V i=1 i i |
|
|||
де RI- – радіус-вектор i-ї частинки, Fi – |
повна сила, що діє на частинку |
|||||
i збоку усіх інших частинок, і сума береться за усіма N частинками (в двовимірному випадку дріб 1/3 замінюється на 1/2).
За даними МК моделювання, віріал сили зручно представити через ПФРРА, g(r), та похідну від потенціалу. Розглянемо суму добутків радіус-векторів й сил з урахуванням Nk атомів відносно кожного і-го обраного атома (напрямки радіус-векторів і сил збігаються):
|
N |
|
|
∞ |
|
∑rik ×Fik = |
∑rk × Fk (rk ) ; ∑ rk ×Fk (rk ) @ ∫ r F dN , |
||||
2 |
|||||
i,k |
k |
k |
0 |
||
де dN = 4pr2 g(r)dr × r0 , |
r0 = N /V . Тому |
|
|||
210
