
Ovru-all
.pdf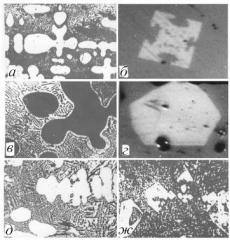
dV= ∑ωidhi =0. |
(6.3) |
i |
|
Розписавши повний диференціал від об’єму формально та врахувавши (6.3), знаходимо, що ∑ hidωi = 0. А мінімум від виразу для пове-
i
рхневої енергії (6.2) дає ∑ γidωi =0. Останні дві рівності виконуються
i
одночасно, якщо hі~γі.
Таким чином, чим меншою є поверхнева енергія, тим ближче грань знаходиться до центра кристала і тим більша її площа порівняно з іншими гранями. Поверхнева енергія мінімальна для граней, що відповідають щільно упакованим атомами кристалічним площинам. Ці грані є основними в габітусі кристала.
Зі збільшенням температури (наприклад, при русі вгору вздовж лінії ліквідусу зі зміною складу бінарних розплавів ближче до основного компонента), з’являються додаткові грані і поступово збільшується їх відносна площа. А згодом можуть з’явитися округлі ділянки. З чистих розплавів металів зазвичай ростуть округлі кристали, а огранювання з’являється при зниженій температурі і певному складу розплаву (рис. 6.5), пов’язаних між собою умовами рівноваги – лінія ліквідусу на діаграмі стану.
Рис. 6.5. Форми росту кристалів у слабко пересичених розплавах [2, 3],
а, б – срібло, температура Т=700 та 450 К; в, г – мідь, Т=700 та 480 К; д, ж – алюміній, Т=580 та 400 К.
161
6.2.Атомна будова поверхні кристалів
6.2.1.Час життя та дифузія адатомів поверхнею кристала
У5 розділі розглядалася адсорбція молекул газу на поверхні твердих тіл. Якщо кристал знаходиться у контакті зі своєю парою, адсорбція також має місце. На впорядкованих гранях кристалів зайняті майже всі можливі місця у відповідній кристалічній площині (вона може бути реконструйованою (розділ 3). Ті атоми, що приєднуються
зпари, мають обмежену кількість зв’язків, і тому час їхнього життя на поверхні недовгий. На поверхні встановлюється динамічна рівновага між кількостями атомів, що осаджуються і залишають поверхню.
Як вже зазначалось вище, кількість атомів, що падає із газу на
одиничну площу поверхні, пропорційна тиску, I1= |
|
P |
|
, де m – |
|
|
|
||
2πmkT |
маса молекул; k – стала Больцмана; T – температура.
Десорбція (або випаровування) молекул відбуватиметься лише із зайнятої частини поверхні, інтенсивність потоку, що випаровується пропорційна концентрації осаджених атомів ns, І2=fns, величина f – частота відривів адсорбованих атомів залежить від частоти їх коливань υ та фактора Больцмана від величини енергії адсорбції Uа , f= υexp(–uа/kT).
Час життя атомів на поверхні τs можна визначити, покладаючи ймовірність їх відриву рівною одиниці
Р‾=υexp(–uа/kT) τs =1,
(величина υexp(–uа/kT) τs дає ймовірність відриву атома за час одного коливання). Звідси знаходимо
τs= (1/υ) exp(uа/kT) =τ0 exp(uа/kT), |
(6.4) |
де τ0 – час одного коливання.
Структура поверхонь кристалів така, що адатоми знаходяться над заглибленнями між атомами нижнього шару. В таких місцях вони взаємодіють з декількома атомами нижнього шару, а отже, знаходяться у потенціальних ямах. Для перескоку адатома у сусіднє заглиблення необхідно подолати потенціальний бар’єр uд. Цей бар’єр
менше за енергію uа. Тому за час життя τs адатоми виконують багато стрибків і переміщуються на відносно значні відстані. Час життя атома в одній потенціальній ямці
162

τд=(1/υ)exp(uд/kT)=τ0 exp(uд/kT). |
(6.5) |
Застосуємо формулу Ейнштейна (<x2>=2D t) спочатку до перемі-
щення, пов’язаного з одним стрибком: а2=2Dsτд, Ds=а2/2τд. А потім знайдемо середнє переміщення:
T |
|
|
|
τs |
T |
|
|
T |
|
τs |
|
ua − uд |
|
λ2 |
= 2D τ |
|
= a2 |
, λ |
|
= |
λ2 |
= a |
= aexp( |
). (6.6) |
|||
|
|
|
|
||||||||||
s |
s |
s |
|
τд |
|
s |
|
s |
|
τд |
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
||||
Час одного коливання τ0 складає ~10–13 |
с, uа 0.4 Ηвип. Для крис- |
||||||||||||
тала цинку за температури 600 К маємо τs 10–7 с. Оскільки uд 0.1 uа, маємо оцінку для середніх температур λs 103 а. Зі зменшенням температури середній пробіг збільшується й може сягати 10–5 ÷10–2 см.
6.2.2. Структура сходинок на поверхні кристала.
Я.І. Френкель [4] ще у 20 роки 20 сторіччя подав ідею, що теплові флуктуації можуть впливати на структуру сходинок, будучи причиною утворення зламів, поняття про які було уведено Косселем та Странським. На рис. 6.6. показано результати Монте-Карло моделювання структури поверхні кристала Косселя (проста кубічна гратка)
зі сходинкою за різних температур (відношень Η/kT). Спочатку пряма сходинка із часом стає ламаною внаслідок утворення зламів. На поверхні з’являються адатоми та дірки, виникають кластери з адатомів. За підвищених температур поверхня перестає бути різкою, а становить собою перехідну зону із декількох атомних шарів.
Рис. 6.6. Переріз міжфазної межі в площині, яка містить сходинку [5], a – Η/kT=4.9, σ=Δμ/kT=0.1;
b – Η/kT=3, σ=0.02; c – Η/kT=2,7, σ=0.004.
Наведені в підписах до рисунку значення Η/kT характерні для меж кристал-розплав. У випадку границі кристал-пара ці значення набагато вищі, а структура поверхні значно більш впорядкована.
Наведемо аналіз шорсткості сходинок згідно [1]. Мірою шорсткості сходинок приймемо відношення (U–U0)/U0, де U0 – потенціальна енергія прямої сходинки без зламів, а U–U0 – зміна енергії за
163
рахунок утворення зламів, атоми зламів мають менше зв’язків типу s-s (для кристала Косселя менше на 1 зв’язок). Позначимо через ε енергію обірваного зв’язку, γl – крайову енергію (в розрахунку на одиницю довжини) сходинки, n – загальна кількість місць на сходинці, U0=nε для кристала Косселя, n+ – кількість зламів уверх (сходинка {10}), n– – кількість зламів униз, n0 – кількість місць на сходинці без зламів. Для прямої сходинки n+=n– =nз. Тому 2nз+n0 = n.
Ентропію шорсткої сходинки знаходимо за формулою Больцмана
S=k lnW, де термодинамічна ймовірність |
|
n! |
= |
n! |
|
W= |
|
|
. |
||
n0 !n+ !n− ! |
n0 !(n3 )2 |
||||
Відповідно, γl =U–TS=nε+2nзε–kT[nln(n/e)–n0ln(n0/e)–2nзln(nз/e)] (тут враховано формулу Стірлінга ln(n!)=nlnn–n ).
Шукаємо рівноважну структуру, для цього знаходимо мінімум від виразу для γl:
дγl/дnз =2ε–kT[2n0ln(n0/e)–2ln(nз/e)]=0,
тут враховано, що д/дnз= –2д/дn0. З останньої рівності визначаємо
|
n |
|
= e− |
ε |
|
|
|
|
|
|
|
|
n |
|
nη |
|
||
|
з |
|
= η , тоді 2n0 η+n0 = n, n0 |
= |
, n3 = |
. |
||||||||||||
|
kT |
|||||||||||||||||
|
|
|
|
|
||||||||||||||
|
n0 |
|
|
|
|
|
|
|
2η + 1 |
2η + 1 |
||||||||
Відстань між зламами |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
λз=1/2nз= |
an |
= |
a |
|
1 + 2η |
= |
a |
(2 + exp(ε /kT) ). |
(6.7) |
||||||
|
|
|
2n3 |
2 η |
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
Для границі кристала з газом Ηвип/kTпл 25÷30, ε/kTпл 4÷5. За середніх температур λз=(10÷100)а, за низьких температур
λз=(104÷106)а. У разі межі кристал-розплав теплота переходу значно менша, а шорсткість сходинок значно більша.
Перепишемо вираз для γl у вигляді:
γl=nε+2nзε–kT [n0ln(n/n0)–2nзln(n/nз)]. |
|
Враховуючи вирази для відношень n0/n та nз/n, маємо |
|
γl=nε–2nз kTln(1+2η)–n0kTln(1+2η)]. Або остаточно: |
|
γl=nε–n kTln(1+2η)=–n kTln(η(1+2η)). |
(6.8) |
За низьких температур γl>0 завжди, тому що nε>0. При підвищені температури крайова енергія зменшується і при температурі Тш, за
164
якої η=0.5 γl перетворюється на нуль. Очевидно, ε/kTпл=0.7,
Η/kTпл=4.2. За цієї і вищих температурах на поверхні можуть безбар’єрно утворюватись будь-які кластери, тому що енергія границь, що їх обмежує, дорівнює нулю. Така поверхня буде шорсткою й багатошаровою. Щоправда, коли ширина міжфазної межі прямує до нескінченності, окреме існування фаз неможливе. Розгляд шорсткості сходинок у моделі, що допускає злами висотою у два атоми, при-
зводить до відношення ε/kTпл=0.8 і, відповідно, до Η/kTпл=4.8.
6.2.3.Шорсткість граней кристалів.
Впопередньому підрозділі ми дійшли висновку, що грані кристалів, які межують із власною парою, є слабко шорсткими: кількість адатомів та дірок на їхніх поверхнях мала, а сходинки містять порівняно мало зламів. Теплота плавлення усіх речовин набагато менша за
теплоту випаровування: Η/kTпл=1÷2 для металів, Η/kTпл=3÷4
для напівпровідників, Η/kTпл=5÷10 для органічних речовин. Щоправда, є декілька металоподібних органічних речовин, наприклад: камфора, камфен, сукцинонітрил. Кристали металів мають найчастіше округлі форми росту (рис. 6.6), що свідчить про значну шорсткість у атомному масштабі між фазної межі. Джексон [6] звернув
увагу, що всі речовини, для яких Η/kTпл>2, мають гранні форми росту. Аналіз даних форм росту кристалів з бінарних розплавів [3] показав, що переходу від гранних до округлих форм росту відповідає
значення відношення Η/kT>1.35±0.05. Але ж в попередньому підрозділі був отриманий значно вищий критерій шорсткості ( Η/kTпл=4.2). Тому шорсткість поверхонь кристалів аналізувалася багатьма авторами, їй була присвячена велика кількість робіт з моделювання.
Бартон Кабрера і Франк [7] застосували до поверхні кристала Косселя розв’язок Онсагера для двовимірної моделі феромагнетику
Ізінга й отримали, що Η/kTпл=5.1. Вони також розглядали поверхні з декількома шарами й аналізували упорядкування у квазіхімічному наближенні. Але значення безрозмірної ентропії S/k= Η/kTпл, все одно, були надто високими.
Вагомий вклад у теорію був внесений роботами Темкіна [8]. Він розглядав міжфазну межу кристала Косселя довільної ширини у наближенні Брегга-Вільямса, тобто без урахування упорядкування при запису ентропійної складової (як це зроблено вище для сходинки).
165

Мінімізація виразу для вільної енергії такої межі дозволила дослідити вплив основного параметру εsl на розподіл концентрації умовно «твердих» атомів у напрямку, перпендикулярному до міжфазної межі (від номеру шару). Пізніше іншими авторами був проведений аналіз з урахуванням упорядкування в послідовних шарах, а також Монте-Карло моделювання такої поверхні. У всіх цих роботах було заборонено розміщення твердих атомів над рідкими. На рис. 6.7 відображені результати, отримані для двох значень параметра
ξ=4εsl/kT. Обидва профілі концентрації відповідають шорстким поверхням. Відповідно до результатів Темкіна [8] (нульове наближення), критерій переходу від шорсткої до гладенької поверхні
Η/kTпл=3.6.
Рис. 6.7. Залежності долі заповнених вузлів xi від номеру шару i для по-
верхні розділу кристала Косселя з парою, грань (100),
● – нульове наближення [8], ▲ – перше наближення (квазіхімічний метод), I – МК моделюванням [9].
В навчальній літературі знайшла відображення найпростіша модель міжфазної межі з одним перехідним шаром, запропонована Джексоном [6]. Нехай у такому шарі кількість місць дорівнює N, а кількість «твердих» атомів Ns. Якщо всі тверді атоми розміщені разом одним острівцем, поверхня повністю впорядкована. Запишемо вираз для зміни вільної енергії, якщо ми розкидаємо тверді атоми по поверхні
F= U–T S= Nszsεsl(1 − x)− kT ln |
N! |
, |
|
Ns!(N − Ns )! |
|||
|
|
де вираз для ентропії записаний згідно з формулою Больцмана (термодинамічна ймовірність є числом розміщень «твердих» та «рідких» атомів по N місцях); х=Ns/N, (1–x) – частка рідких атомів. Застосовуємо формулу Стірлінга й розділюємо все на NkT:
F |
= |
zsεsl |
x(1 − x) + xln x + (1 − x)ln(1 − x) . |
(6.9) |
NkT |
|
|||
|
kT |
|
||
166

На рис. 6.8 показані залежності F від х при різних значеннях па-
NkT
раметра α= zsεsl . Всі криві мають екстремум за х=0.5. При малих α kT
це мінімум, а при великих – максимум. При великих α є ще два мінімуми, що відповідають або малим, або великим (близьким до 1) значенням х. Джексон дав таке трактування наведених кривих. При ве-
ликих α мінімуму вільної енергії відповідає гладенька поверхня з малим, або близьким до одиниці вмістом «твердих» атомів у перехі-
дному шарі. При малих значеннях α є тільки один мінімум при х=0.5, який відповідає шорсткій поверхні – однакова кількість «твердих» та «рідких» атомів, розміщених невпорядковано.
Знаходимо значення х, що відповідає мінімуму вільної енергії:
∂( F )
NkT = α(1 − 2x) + ln x − ln(1 − x) = 0
∂x
х=0.5.
Перехід від кривих з максимумом до кривих з мінімумом проходить по кривій з точкою перегину при х=0.5. Розписуємо другу похідну, підставляємо значення х=0.5 і знаходи-
мо значення α=2, що відповідає такому пе- Рис. 6.8 [6] реходові. Отже, в найпростішій моделі
отримане значення Η/kTпл=(3/2)α=3, що менш відрізняється від експериментальних даних. Швидше за все, припущення Vsl Vll при розрахунку параметра εsl через теплоту плавлення є некоректним. А
насправді значення εsl значно більші за рахунок пониженої густини міжфазної межі. І це призвело до парадоксу погіршення результату при покращенні теорії. Оскільки роботи з моделювання за методом Монте-Карло виходили з тих самих припущень, вони не призвели до покращення результату.
167
6.3. Поверхнева кінетика
6.3.1. Рух одиночної сходинки
Поверхня кристалів може бути гладенькою або шорсткою в атомному масштабі в залежності від температури та середовища, яке їх оточує. У випадку гладеньких поверхонь, структура і форма сходинок, що існують (біля виходу гвинтових дислокацій) або з’являються на поверхні, значною мірою визначають кінетику росту за пошаровими механізмами – дислокаційним чи механізмом двовимірного зародкоутворення.
Френкель [4], а згодом Бартон, Кабрера і Франк [7] показали, що на відміну від плоскої грані, сходинки, які за температури 0 К є прямими, зазнають «плавлення» із підвищенням температури (задовго до точки плавлення), тобто стають шорсткими; це «плавлення» полягає в утворенні численних зламів. Середню відстань між зламами сходинок можна розрахувати за формулою (6.7). Оцінки для типових речовин і температур дають високу концентрацію зламів, так що сходинку можна розглядати як безперервний стік для адатомів у процесі росту кристалів.
При розгляді росту кристалів з пари імовірність прямої конденсації в злам сходинки приймають малою. Вважають, що швидкість росту визначається дифузією адатомів до сходинки з деякої ділянки
поверхні (шириною λS з двох сторін від сходинки, причому λS –
середня довжина дифузійного пробігу адатома за час життя на поверхні). Аналіз у такій моделі призводить до наступного виразу для швидкості росту прямої сходинки:
V∞ = 2σ ν0 λs |
|
− |
Hвип |
(6.10) |
exp |
, |
|||
|
|
|
kT |
|
де σ=Δμ/kT – пересичення; ν0 – частота, близька до частоти коливань атомів у кристалічних ґратках.
При рості з розчинів або розплавів існує можливість прямого приєднання молекул до зламів. В силу складності врахування декількох процесів: активаційного приєднання, дифузії до сходинки в об’ємі розплаву або розчину і поверхневої дифузії, будемо швидкість росту сходинки описувати простим співвідношенням
V∞ = βstσ , |
(6.11) |
де σ – локальне поверхневе пересичення (σ=ln(C/Ce) для розчину,
168

σ= H T/(kTe2) для розплаву); βst – кінетичний коефіцієнт сходинки. Оскільки поблизу опуклої сходинки рівноважна концентрація або температура мають бути більше, ніж поблизу прямої (за аналогією з формулою Томсона для тривимірного випадку), швидкість росту такої сходинки можна виразити через швидкість росту прямої [7]:
V(r) = V |
|
1 − |
rкр |
|
, |
(6.12) |
|
|
|||||
∞ |
|
r |
|
|
|
|
|
|
|
|
|
|
|
де rкр=a γst /(kTσ) – радіус критичного двовимірного зародка; γst – вільна крайова енергія сходинки висотою а в розрахунку на одну молекулу.
6.3.2. Дислокаційний механізм росту.
Як показав Франк, якщо гвинтова дислокація має складову вектора Бюргерса, перпендикулярну до поверхні, то перетинання такої дислокації з поверхнею веде до виникнення сходинки, що не може зникнути під час росту кристала. Сходинка закріплена в точці перетину дислокації з поверхнею, однак мірою приєднання атомів чи молекул сходинка може переміщуватися, утворити спіраль і, відповідно, певний виступ у вигляді конуса на грані. Спіраль закруглюється доти, доки кривизна в центрі не досягне 1/rкр, відповідно до (6.12), після чого вся спіраль – " обертається", зберігаючи свою форму.
Стаціонарна спіраль приймає приблизно форму архімедової; у полярних координатах така спіраль описується формулою r = 2rкрθ .
Таким чином, з кожним витком обертання сходинка переміщається
на 4πrкр , затрачаючи на це час 4πrкр = 2π , де ω – кутова швидкість
V∞ ω
обертання спиралі. Тому нормальна швидкість росту кристала виразиться у вигляді [7]
V = |
aω |
= |
aV |
= |
β kT |
σ |
2 |
|
|
|||
|
|
|
∞ |
|
|
|
. |
(6.13) |
||||
2 |
π |
4πr |
4π γ |
st |
|
|||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
кр |
|
|
|
|
|
|
|
Параболічний закон росту чинний, якщо відстані між сходинками спіралі досить великі (випадок малих пересичень). При збільшенні пересичення і, відповідно, зменшенні відстаней між сходинками через перекриття дифузійних полів поблизу сходинок швидкість росту збільшується повільніше з ростом пересичення, і закон росту наближається до лінійного. Точніший розрахунок [10] відстаней між сходинками дає замість 4πrкр у знаменнику (6.13) значення 19rкр .
169

6.3.3. Ріст за механізмом двовимірного зародкоутворення
Двовимірні зародки, тобто дископодібні чи обмежені прямими ребрами кластери, розростаючись поверхнею кристала, призводять до відкладення нових шарів. Частота виникнення круглих зародків
[1, 11, 12]
|
3 |
1 |
|
|
|||
h 2 |
|
||||||
I = |
|
|
|
βσ |
2 |
exp |
− |
|
|||||||
Ω |
|
|
|
|
|||
|
|
|
|
||||
|
πγ |
2 |
|
|
|
|
|
|
|
|
st |
|
|
, |
(6.14) |
|
2 |
|
2 |
|
|||
k |
|
|
|
|
|
||
|
Te |
σ |
|
|
|||
де в показнику експоненти є робота утворення двовимірного зародка критичного розміру, поділена на kT: exp(–δΦ(n*)/(kT)); h – висота сходинки, утвореної двовимірним зародком, Ω – об’єм, що приходиться на один атом; Te – рівноважна температура. Швидкість росту
грані площею l 2 у випадку утворення нових шарів поодинокими двовимірними зародками [1]:
|
|
|
|
|
h |
3 |
|
1 |
|
|
|
|
|
|
|
4 |
|
|
|||||
VI = hl |
2 |
I = hl |
2 |
|
βσ |
2 |
|
− |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
exp |
||||||
|
|
|
|
|
Ω |
|
|
|
|
|
|
πγ 2 |
|
|
|
|
st |
|
|
, |
(6.15) |
k2T 2 |
|
|||
σ |
|
|
||
e |
|
|
|
|
У випадку, якщо зростаюча грань вкрита численними зародками (велика частота їхнього виникнення), новий шар виникатиме, коли нижче розміщений є ще не цілком заповненим, тобто буде відбуватися утворення зародків на поверхні розміщених зародків, що розростаються. Нехай деякий зародок (надкритичний) росте з постійною швидкістю. Нехтуючи його малим початковим розміром, приймемо,
що в момент часу t він вкриває площу πV∞2t2 .Число нових зародків, виникаючих на його поверхні, дається формулою
t |
|
n1 = ∫ IπV∞2t2 dt . |
(6.16) |
0 |
|
Визначимо час очікування τоч, як середній час, при якому число нових зародків, що утворилися, дорівнює 1. Тоді
|
|
τоч |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
∫ πIV∞2t2 dt = 1 ; τоч = (IV∞2 )− |
|
|
і |
|
|
||||||||||
|
|
3 |
|
|
|||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
5 |
|
|
|
πγst2 |
|
|
||||
|
h |
|
|
h3 |
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
VII = |
|
h(IV∞ )3 |
= |
|
|
βσ6 |
exp |
− |
|
|
|
|
. (6.17) |
||||
τоч |
Ω |
|
2 |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
3k Te |
σ |
||||||
Цією формулою прийнято описувати ріст за механізмом двовимірного зародкоутворення за підвищених пересичень. Формула
170
