
Ovru-all
.pdf
Згадані вище функції, що входять до потенціалу Терзоффа для кремнію мають вигляд [14]:
bij = (1 + βnξijn )−1 / 2n ; ξij = ∑ fc (rij )g(θijk )exp λ33 |
(rij − rik )3 |
; |
|||||
|
k¹i, j |
|
|
|
|
||
g(θijk )= 1 + |
|
|
|
|
|
||
c2 |
c2 |
|
|
|
|||
|
− |
d2 + (h − cosθijk )2 |
, |
|
|
|
|
d2 |
|
|
|
||||
Основні параметри потенціалу |
такі: A=3264.7 еВ, B=95.373 еВ, |
||||||
λ1=3.2394 Å -1, λ2=λ3=1.3258 Å -1, |
β=0.33675, c=4.8381, |
d=2.0417, |
|||||
n=22.956. |
|
|
|
|
|
||
Потенціали Стілінджера-Вебера, Кітінга і Терзоффа цілком успішно застосовуються до кремнію. Загальною проблемою усіх потенціалів є складності їх застосування за інших умов, ніж ті, для яких вони були створені.
1.2.6. Похибки, притаманні методу Монте-Карло
Як і кожний наближений метод, метод Монте-Карло потребує оцінки точності отриманого результату, тобто оцінки відносної похибки середньої величини, що обчислюється. Методу Монте-Карло властиві як систематичні похибки, характерні для детермінованих наближень без використання елементу випадковості, так і похибки іншого роду – статистичні. Перші пов’язані з ідеалізацією моделі, наприклад, зі скінченністю числа ступенів вільності модельованої системи, з неточностями в постановці чисельного експерименту, з недосконалістю генераторів випадкових чисел і т. д. Другі виникають з тієї причини, що середнє за кінцевим інтервалом Маркового часу, тобто за кінцевим числом кроків процесу, є величиною випадковою, флуктуючою, і збігається до точного середнього лише в граничному випадку нескінченого часу вимірювання. Наприклад, величина <Е>N — випадкова; вона має розкид, ширина якого спадає зі
збільшенням N. Кількісно ширина розкиду δЕN обчислюється як стандартна похибка в теорії похибок
|
1 |
N |
|
|
|
|
δЕN = { |
− < E >i ] }1/2 =σ/ N , |
|
||||
|
∑[Ei |
(1.30) |
||||
|
||||||
|
N(N - 1) i=1 |
|
|
|
|
|
де Еi – « миттєве» значення вимірюваної величини;
31
<Е>i – « миттєве» значення середньої величини після i вимірювань;
σ – дисперсія, тобто середньоквадратичне відхилення значень енергії від її середнього значення.
З (1.30) можна бачити, що розкид значень середньої енергії дорівнює дисперсії її випадкових значень, поділеної на корінь з числа вимірювань. Формула (1.30) наочно характеризує одну з головних особливостей методу Монте-Карло: похибка обчислень спадає пропорційно кореню з реального часу роботи ЕОМ в даному статистичному експерименті. Таким чином, для збільшення точності обчислення будь-якої фізичної величини на один десятинний знак, потрібен, простіше кажучи, в 100 разів швидший комп’ютер.
Чисельне моделювання об’єктивно містить у собі ряд принципових труднощів. Суттєвою проблемою є вибір оптимального потенціалу взаємодії i пов'язане з його функціональною формою масштабування величин. При моделюванні атомних ансамблів доводиться оперувати величинами, що мають дуже низький порядок (m~10–26 кг, r~10–10 м, Е~10–20 Дж). Зазвичай в методі МК масштабуються положення частинок i енергія системи, а оскільки всі інші використані величини пов'язані з ними, можна прийти до безрозмірних рівнянь. Положення частинок нормуються на мінімальну відстань між частинками в реальних кристалічних гратках. Енергія системи нормується на характерний параметр, що входить до потенціалу взаємодії між частинками.
1.3. Застосування методу молекулярної динаміки до систем з великої кількості атомів
1.3.1. Загальна характеристика методу
Метод молекулярної динаміки (МД) було розроблено у 1957 році в роботі Олдера та Вайнрайта [15]. Він достатньо детально розглядається в багатьох роботах (див., наприклад, [11,16-18]). Метод МД дозволяє досліджувати системи за температур Т>0 K. Моделлю речовини (фази) є сукупність частинок в деякому об’ємі. На кожному
кроці за часом (крок ітерацій ≈10-15с) визначаються сили, які діють на частинки, знаходяться їх рівнодіючі значення, розраховуються прискорення частинок й приріст швидкостей, а потім усі частинки одночасно зміщуються у нові положення. Сили, які діють на частинки, можуть бути задані аналітично у вигляді формул, до яких входять відстані між атомами, або ще й кути між трійками атомів. Інший ва-
32
ріант – коли сили задані у вигляді таблиць значень, які відносяться до послідовних відстаней з постійним кроком (скажімо, δr 0,1Å). У цьому випадку необхідна відповідна інтерполяція даних таблиці на фактичні значення міжчастинкової відстані для конкретної пари частинок. Міжчастинкові сили можуть бути розраховані квантовомеханічно, або знайдені із відомих дифракційних даних про структуру досліджуваної системи [11,17].
Для пошуку рівнодіючих сил (фактично розраховуються проекції сил на осі координат) необхідно проводити перебір пар (або трійок) атомів, що займає левову частку часу розрахунків в методі МД. У випадку короткодіючих сил можна ввести радіус обрізання взаємодії rс і розраховувати ті пари, відстані між якими не перевищують rс.
Реальні системи складаються з великої кількості взаємодіючих одна з одною частинок. Хоча міжмолекулярні сили породжують складні траєкторії руху кожної молекули, властивості речовини безпосередньо від них не залежать. Вони пов'язані з усередненими характеристиками молекулярного руху. Ні на якому суперкомп'ютері майбутнього не можна буде розв’язати мікроскопічні рівняння руху для 1025 взаємодіючих між собою частинок. Однак і в системах з декількох тисяч атомів багато явищ відбувається подібно до того, як це має місце в макроскопічних системах. Метод МД застосовують зараз до систем, що нараховують зазвичай від декількох тисяч до декількох десятків тисяч частинок, і він вже багато дав для усвідомлення спостережуваних властивостей газів, рідин і твердих тіл.
Які основні властивості й закономірності проявляються в системах багатьох часток? Які параметри потрібно використовувати для опису таких систем? Такі питання розглядає статистична фізика, і основні її принципи мають бути відомими для дослідника, що вико-
ристовує метод молекулярної динаміки.
1.3.2. Алгоритми чисельного розв’язку рівняння руху
Основний зміст другого закону Ньютона полягає в тому, що він виражає рівняння руху
ma = m(d2r/dt2)=F(r(t)), |
(1.31) |
де r(t) – радіус-вектор частинки. Воно набуває сили тільки при відомій функції F(r(t)), записаній у правій частині рівняння (1.31). Тоді можливо його інтегрування. Якщо задані початкова швидкість та ко-
33
ординати частинки, можна визначити їхні значення в інші моменти часу.
Найпростіший метод числового розв’язку цього рівняння (метод Ейлера) полягає в тому, щоб, вибравши малий крок за часом t, визначати прирощення радіус-вектора й вектора швидкості з рівнянь:
R |
= V |
× Dt, |
|
|
|
|
Dr |
|
|
|
|||
R |
R |
1 |
R |
R |
(1.32) |
|
DV = aDt = |
|
F(r |
(t))Dt. |
|||
m |
||||||
Повторюючи такі обчислення, отримуємо послідовні значення координат та компонент вектора швидкості в момент часу tn+1=tn+Δt, наприклад для координати x,
xn+1 = xn+vn t . |
(1.33) |
Точність числового розв’язку рівняння руху за методом Ейлера та при застосуванні інших аналогічних методів залежить від величини кроку за часом t. Цей крок має бути достатньо малим, для того щоб похибки числового розв’язку були невеликими і результати задовольняли законам збереження енергії та імпульсу. В інших методах розрахункові формули дещо ускладнюються, наприклад, у виразі для координат уводиться доданок з прискоренням, для розрахунку швидкості береться середнє прискорення на проміжку часу t. У результаті точність розв’язку дещо підвищується, але розрахунків стає більше. Проста зміна виразу (1.33) полягає в тому, щоб визначати xn+1 через vn+1 – швидкість в кінцевій точці інтервалу, а не в початковій точці. Запишемо такий модифікований метод Ейлера в наступному вигляді (для спрощення запису розглядатимемо одномірний рух):
vn+1 = vn+anDt, |
(1.34а) |
xn+1 = хn+vn+1Dt. |
(1.34б) |
Оскільки алгоритм (1.34), був детально розглянутий Кромером, його називають методом Ейлера-Кромера. Кромер назвав вирази (1.33) й (1.34) апроксимаціями за першою точкою й за останньою точкою.
Мета усіх кінцево-різницевих методів полягає в розрахунку значень vn+1 й xn+1 (точка в фазовому просторі) в момент часу tn+1=tn+Δt. Величину кроку за часом t=Δt необхідно вибирати таким чином, щоб інтегрування давало стійкий розв’язок. Один зі способів перевірки стійкості методу полягає в контролюванні величини повної енер-
34
гії й забезпеченні того, щоб вона не відхилялась суттєво від початкового значення. Завищене значення кроку t призводить до числових розв’язків, які з плином часу все більш відхиляються від істинного. Алгоритми Ейлера й Ейлера-Кромера не забезпечують збереження енергії за досить великий час моделювання. Зменшення кроку за часом підвищує точність розрахунків, але за дуже великої кількості кроків за часом накопичуються похибки округлення.
Відмінність алгоритмів методу МД полягає у способі розрахунку нових координат і швидкостей наприкінці кроку. Це – стандартна задача чисельного інтегрування рівнянь руху, і для її розв’язку можливо застосовувати розрахункові схеми різного порядку, наприклад, формули Рунге-Кутта, методу предиктор-коректор і т.п. Достатньо точним є простий алгоритм Л. Верле, який дозволяє розраховувати координати i-ї частинки в кінці кроку через її координати на початку даного й попереднього кроків. Важливо мати на увазі, що успішне використання чисельного методу визначається не тільки тим, наскільки добре він наближає похідну на кожному кроці, але й тим, наскільки добре він апроксимує інтеграли руху, наприклад, повну енергію.
Суть багатьох алгоритмів можна зрозуміти, розкладаючи vn+1=v(tn+ t) та xn+1=x(tn+ t) у ряд Тейлора
vn+1 = vn + an t + O(( t)2), |
(1.35) |
xn+1 = xn + vn t +½ an( t)2 + O(( t)3). |
(1.36) |
Добре відомий метод Ейлера еквівалентний збереженню в (1.36) членів О( t). Тому локальна похибка (похибка на кроці) становить
величину О( t)2. Однак від кроку до кроку похибки накопичуються, тому вважають, що глобальна похибка методу Ейлера, що представляє собою сумарну похибку за розглянутий проміжок часу, буде величиною О(Δt). При цьому враховують, що число кроків, на яке роз-
бивається часовий інтервал, пропорційно 1/ t. Отже, глобальна похибка більше за локальну. Прийнято вважати, що метод має n-й порядок апроксимації, якщо його локальна похибка дорівнює
O(( t)n+1), тому метод Ейлера відноситься до методів першого по-
рядку.
Алгоритм Ейлера-Кромера (1.34) (наближення за останньою точкою) має ті самі вади, що й метод Ейлера. Очевидний шлях поліпшення методу Ейлера полягає у використанні для обчислення нового
35
значення координати середньої на відрізку швидкості. Відповідний метод середньої точки можна записати у вигляді
vn+1 = vn + an t, |
(1.37а) |
xn+1 = xn +½(vn+1+vn) t. |
(1.37б) |
Зазначимо, що якщо підставити вираз (1.37а) для v в (1.37б), то одержимо
хn +1= xn +vn t + ½ an ( t)2. |
(1.38) |
Отже, метод середньої точки – метод другого порядку точності за координатою й першого порядку точності за швидкістю.
До методів більш високого порядку точності з обмеженою похибкою відноситься метод півкроку.
vn+½= vn-½+an |
t, |
(1.39а) |
xn+1= xn+ vn+½ |
t. |
(1.39б) |
Тут зміна координати знаходиться через середню на даному кроці швидкість. Метод півкроку не самостартує, тобто для початку роботи програми потрібно знати v½. Для першого кроку можна поклас-
ти v½= v0+ ½ a0 t.
Один з найбільш відомих алгоритмів високого порядку точності був розроблений Л. Верле [19] й називається алгоритмом Верле. За аналогією з (1.36) запишемо розкладання в ряд Тейлора для xn-1
xn-1= xn – vn t +½ an(( t)2). |
(1.40) |
Якщо скласти формули інтегрування вперед та назад (вирази (1.36) і (1.40) відповідно), то одержимо
xn+1 = 2xn – xn-1+ an(( t)2) +O(( t)3). |
(1.41) |
Аналогічне врахування розкладань у ряд Тейлора для (xn+1 - xn-1) дає
vn =(xn+1 – xn–1)/(2 t). |
(1.42) |
Пов'язана з алгоритмом Верле (1.41, 1.42) локальна похибка має
третій порядок для координати й другий порядок для швидкості.
Однак швидкість не бере участь в інтегруванні рівнянь руху. У літературі з чисельного аналізу алгоритм Верле (1.42) називається – неявною симетричною різницевою схемою.
Недоліком останнього алгоритму є те, що він не самостартує, і необхідно використати інший алгоритм для одержання декількох
36
перших точок фазового простору. Ще один недолік полягає в тому, що нова швидкість знаходиться по формулі (1.42) через різницю близьких за величиною чисел. Така операція обумовлює втрату значущих цифр і може призводити до значного росту похибки округлення.
Математично еквівалентною версією алгоритму Верле є схема
xn+1 = xn + vn t + ½an(( |
t)2), |
(1.43a) |
vn+1 =vn +½(an+1 + an) |
t. |
(1.43б) |
Схема (1.43) названа швидкісною формою алгоритму Верле. Вона самостартує й не приводить до накопичення похибки округлення.
Метод Верле має риси відомого з навчальної літератури методу предиктор-коректор. Наприклад, спочатку передвіщаються нові значення координат
~ |
= xn-1 |
+ 2vn |
t . |
(1.44а) |
предиктор: xn+1 |
Ці координати використовуються для знаходження прискорень ~ an+1 ,
~ |
|
а потім, використовуючи an+1 , отримуються скоректовані значення |
|
vn+1 й хn+1 |
|
коректор: vn+1 = vn +½( an+1 + an) |
t, |
xn+1 = xn + ½( vn + vn+1) t. |
(1.44б) |
Часто використовують метод предиктор-коректор більш високих порядків точності. Тобто повторно корегують швидкості після знаходження xn+1 та нового значення an+1, а потім знову знаходять уточнене значення координати xn+1.
На практиці використовують й інші алгоритми. Наприклад, в алгоритмі Бімана [18] запам’ятовуються не тільки координати, але й також швидкості й прискорення на даному й попередньому кроках. Координати та швидкості в наступний момент часу розраховуються за формулами:
ri (t + τ) = ri (t) + vi (t)τ + (1/6) [4ai (t) – ai (t – τ)] τ2, |
(1.45а) |
vi (t + τ) = vi (t)+ (1/6) [2ai (t + τ) + 5ai (t) – ai (t – τ)]τ. (1.45б)
Порівняно із методом Верле у швидкісній формі метод Бімана потребує тільки один додатковий масив прискорень усіх атомів. Але похибки розрахунків при його застосуванні значно знижуються (у випадку потенціалу Леннарда-Джонса добре зберігається енергія).
37
Відомі алгоритми й більш високого порядку: наприклад, алгоритми Ральстона та Вільфа (запам’ятаються дані для 4-х попередніх моментів часу) [16,18], Рамана і Стіллінджера (на кожному кроці розраховуються п’ять похідних від координат за часом) [16,18], Берне і Харпа (варіант методу Рунге-Кутта) [18]. Однак має сенс використовувати такі алгоритми високого порядку лише в особливих випадках, коли, наприклад, потрібно проводити повернення в часі й необхідна дуже висока точність розрахунків.
Не слід віддавати перевагу якомусь одному алгоритму. Краще обміркувати всі аспекти задачі, наприклад: мінімально необхідне число частинок, число масивів, оптимізація швидкості розрахунку, необхідна точність збереження енергії, спосіб стабілізації температури й т.п., а потім вже підбирати алгоритм. Що стосується результатів моделювання, то помилки, пов'язані з вибором потенціалу взаємодії частинок, як правило, перекривають похибки методу, якщо він не занадто поганий, а крок за часом досить малий.
1.3.3. Додаткові варіанти граничних умов
Якісне моделювання має містити в собі всі характерні риси розглянутої фізичної системи. Кінцевою метою модельних розрахунків є одержання оцінок поводження макроскопічних систем, тобто сис-
тем, що містять N≈(1023÷1025) частинок (на 1 см3). Для таких систем частка поверхневих частинок мала й поверхня не впливає істотно на об’ємну структуру. Для системи із 1024 молекул з вільною сферичною поверхнею відношення числа поверхневих молекул до загального їх числа складає за порядком величини N2/3/N=N-1/3=10-8 (інакше:
(4πR2/Ω2/3)/(4πR3/3Ω) Ω1/3/R), де Ω – об’єм молекул).
У порівнянні із цим кількість частинок, яку можна вивчати в моде-
лях методу МД, становить зазвичай 103÷104, і частина атомів поблизу поверхонь або стінок не є дуже малою. Тому не можна поширювати результати моделювання, отримані для резервуарів із жорсткими стінками, на макроскопічні системи. Крім того, якщо атом відбивається від жорсткої стінки, його положення й потенціальна енергія взаємодії змінюються без якої-небудь зміни в його кінетичній енергії. Звідси присутність жорстких стінок означала б, що повна енергія системи не зберігається.
Один зі способів мінімізувати поверхневі ефекти й більш точно змоделювати властивості макроскопічної системи полягає у використанні періодичних граничних умов. До недавнього часу в багатьох
38
роботах дослідники використовували тільки періодичні граничні умови, тому що обчислювальна техніка не дозволяла моделювати системи з досить великою кількістю атомів. Насправді для вивчення багатьох процесів з фазовими перетвореннями періодичні граничні умови за всіма напрямками не підходять [20]. Бажано, щоб система мала вільну поверхню. Нижче буде дано короткий опис різних граничних умов, які застосовують в залежності від розглядуваних явищ.
1. «Періодичні» граничні умови. Вони розглянуті у підрозділі
1.2.4.
2.«Жорсткі» граничні умови. Координати граничних атомів зафіксовані. В цьому випадку передбачається, що достатньо велика кількість рухомих атомних шарів компенсує вплив фіксованості граничних атомів на досліджуване явище. Цей вид граничних умов привабливий своєю простотою, але вимагає великого числа атомів і не дозволяє розв’язувати задачі, пов'язані з істотною зміною термодинамічних параметрів. В методі МД такий вид граничних умов в основному застосовується в комбінації з іншими видами граничних умов.
3.«Підпряжені» граничні умови. Після перетинання атомом границі виникає пружна сила, яка повертає атоми у розрахункову область. При застосуванні цих умов повна енергія системи зберігається. Такі граничні умови зручні при моделюванні реальних газів.
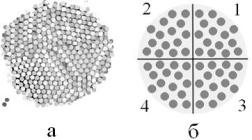
Рис. 1.6. Зразки з вільною поверхнею;
а – закристалізоване залізо з ГЦК структурою,
б– схема ілюстрації дзеркальних граничних умов
4.«Вільні» граничні умови. Приповерхневі атоми утворюють вільну поверхню рис. 1.6,а, що контактує з вакуумом, і можуть пересуватися. Такий вид граничних умов забезпечує встановлення рівноважних міжатомних відстаней для розглядуваних температур і тисків.
При цьому структура приповерхневих шарів відрізняється від об’ємної. Такі граничні умови найзручніші для вивчення поверхне-
39
вих явищ та моделювання фазових перетворень. Якщо є потреба, можна вводити періодичні граничні умови за окремими напрямками, наприклад, при вивчені утворення та властивостей тонких плівок. Наявність хоча б однієї вільної поверхні дозволяє системі досягнути рівноважного стану. Для визначення коефіцієнтів дифузії можна обмежитись періодичними граничними умовами в одному напрямку.
5. «Дзеркальні» граничні умови. Граничні площини відображають розрахункову комірку як у дзеркалі. Частинки не можуть перетнути граничну площину, оскільки відштовхуються своїм образом при наближенні до неї.
Цікавий варіант – розглядати розрахункову комірку у вигляді 1/8 кулі (¼у площині – рис. 1.6,б), щоб вона та її відображення у трьох дзеркальних площинах утворювали повну кулю. При цьому зовнішня поверхня такої кулі була б вільна. Ці умови у 8 разів збільшують кількість частинок у моделі з вільними поверхнями. Недоліком такої моделі є фактична заборона вільного перетинання частинками границь, і є складнощі у підрахунку сил, що діють на частинки поблизу вершини сегмента кулі.
1.3.4. Списки близьких сусідів
Як зазначено у підрозділі 1.3.2, при розрахунку прискорень частинок враховують сили, що діють на частинку з боку інших частинок у межах сфери обрізання потенціалу взаємодії частинок. В таких випадках корисно періодично складати масив найближчих сусідів кожного атома (масив Верле), які знаходяться у сфері з радіусом rv трохи
більшим за радіус обрізання rс. Якщо такий масив обновлюється, наприклад, кожні k0 = 10 кроків за часом, то за цей період жодна інша частинка не повинна проникнути в сферу з радіусом rс. Чим більше k0, тим більше має бути різниця rv - rс. Чим більше різниця rv - rc, тим довше серія ітерацій, що проводиться з одним і тим самим списком найближчих сусідів. При використанні масиву списків Верле швидкість рахунку значно зростає, оскільки не потрібен перебір всіх пар атомів, а тільки пар з атомами, занесених у певний список. Для заданих rv і rс довжина серії k0 визначається дослідним шляхом. Звичайно обирають таке rv, щоб ця довжина перевищувала rс на 10÷20%. Чим більше k0, тим менше час рахунку, що припадає в середньому на одну ітерацію, але тим довше список найближчих сусідів.
40
