
- •Федеральное государственное образовательное учреждение высшего профессионального образования
- •А. А. Нестеров, э.А.Бикяшев теория химического строения и свойства веществ
- •Модуль №1
- •1 Развитие представлений о строении атома
- •Ранние модели строения атома
- •1.2 Квантово-механическое описание атомов
- •1.3 Правила квантования
- •1.4 Правила заполнение электронами атомных орбиталей
- •1.5 Электронное строение атомов в основном состоянии. Связь электронного строения атомов и структуры периодической системы элементов
- •1.6 Закономерности изменения атомных (ионных) радиусов
- •1.7 Закономерности изменения энергий (потенциалов) ионизации
- •1.8 Закономерности изменения сродства к электрону
- •1.9 Электроотрицательности атомов и закономерности их изменения
- •Модуль №2 Электростатические представления в теориях химической связи
- •2.1. Теория электрохимического дуализма
- •2.2. Теория валентности
- •2.3. Теория ионной связи
- •2.3.1. Основные положения теории ионной связи Косселя
- •2.3.2.Оценка энергии ионной связи.
- •2.3.3. Границы применимости теории ионной связи
- •2.3.4 Энергия кристаллической ионной решетки.
- •2.3.5. Ионные радиусы
- •2.3.6. Ионные структуры
- •2.3.6.1. Основные принципы модели жесткой сферы
- •2.3.6.2. Границы применимости модели жесткой сферы
- •2.3.7. Основные свойства ионной связи и её недостатки
- •2.4. Теория поляризации.
- •2.5. Межмолекулярное взаимодействие.
- •Модуль №3
- •3.1. Теория Льюиса и метод олэп.
- •3.2.Основные принципы описания молекул в квантовой химии и метод валентных связей (мвс).
- •3.2.1. Основные принципы описания молекул в квантовой химии
- •3.2.2.Описание механизмов образования химических связей в рамках мвс
- •3.2.3. Описание строения молекул в рамках мвс
- •3.2.5. Дипольный момент и полярность связей
- •3.2.6. Достоинства и недостатки мвс
- •3.3. Метод молекулярных орбиталей (ммо).
- •3.4. Cравнение мвс и ммо
- •Модуль №4 Теория связи в металлах и комплексных соединениях
- •4.1. Химическая связь в кристаллах металлов.
- •4.1.1 Теория «электронного газа».
- •4.2 Зонная теория химической связи для кристаллов металлов, полупроводников и диэлектриков.
- •4.3 Строение кристаллов металлов.
- •4.4 Координационная теория а.Вернера, современная трактовка ее основных понятий и положений
- •4.4.1 Предпосылки создания теории строения комплексов
- •4.4.2 Координационная теория а.Вернера: состав комплексов, поведение в растворах, структура (изомерия)
- •4.4.3 Современная трактовка основных понятий координационной теории
- •4.4.4 Номенклатура комплексных соединений
- •4.4.5 Классификация комплексных соединений
- •4.4.6 Изомерия комплексов
- •4.4.7 Некоторые типы реакций с участием комплексных соединений
- •4.5 Теории химической связи в комплексах
- •4.5.1 Электростатическая (ионная) теория
- •4.5.2 Квантово-механические теории описания химической связи в комплексах
- •4.5.2.1 Метод валентных связей
- •4.5.2.2 Теория кристаллического поля
- •4.5.2.3 Варианты проявления энергетического расщепления орбиталей
- •4.5.2.4 Недостатки ткп
- •4.5.3 Теория поля лигандов (метод молекулярных орбиталей)
- •Заключение
- •Оглавление
4.2 Зонная теория химической связи для кристаллов металлов, полупроводников и диэлектриков.
При описании химической связи в рамках ММО ЛКАО было показано, что при взаимодействии двух атомных орбиталей (АО) образуются две молекулярные орбитали (МО) с различной энергией (связывающая и разрыхляющая). В общем случае число МО равно числу АО, принимающих участие в формировании химической связи. В 1 см3 кристалла металла находиться 1022 – 1023 атомов, т.е. N для данных систем – величина порядка числа Авогадро, что приводит к формированию такого же числа МО, сконцентрированных в малом объёме и, следовательно, отличающихся друг от друга по энергии на ≈ 10-22эВ, т.е. на ничтожно малую величину (рис.10.2)
 число
АО
число
АО
Рис.10.2 - Построение энергетической зоны (совокупности многоцентровых МО) в процессе перекрывания всё возрастающего числа АО.
В связи с этим можно считать, что в процессе взаимодействия атомных орбиталей в системе возникает совокупность делокализованных МО , очень близких по энергии, которая носит название энергетической зоны. В соответствии с принципом минимума энергии в образовании отдельной энергетической зоны в первую очередь принимают участие орбитали с одинаковыми значениями главного и побочного квантовых чисел, а ширина зоны зависит от межатомного расстояния в кристаллической решётке и пространственной направленности орбиталей (рис.10.3).
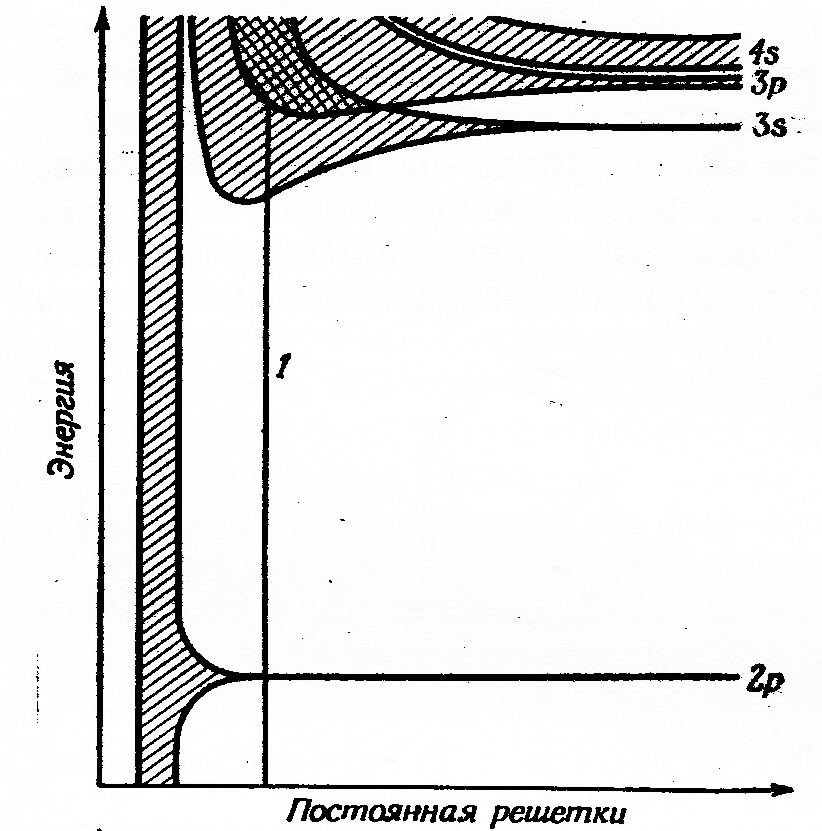
Рис. 10.3 - Расположение энергетических зон в кристаллах натрия, магния и алюминия.
1 – межатомное расстояние в кристалле натрия
Если расстояния между атомами в системе велико, то состояние их электронов описывается АО. При сближении атомов происходит их взаимодействие, т.е. формирование энергетических зон. На каждой МО может разместиться по два электрона с противоположным значением спиновых квантовых чисел. Следовательно, максимально возможное число электронов в зонах, возникающих за счёт перекрывания s-, p-, d- и f – атомных орбиталей (с одинаковым значением главного квантового числа), соответственно равно 2N (s-зона), 6N (р-зона), 10N (d-зона) и 14N (f –зона). Электроны заполняют орбитали зоны, начиная с самых низких по энергии.
В частности, энергия орбиталей 1s, 2s и 2р атомов, образующих кристалл натрия, остаются неизменными при равновесном значении межатомного расстояния в рассматриваемой системе. Орбитали же типа 3s, 3р, 4s и имеющие ещё более высокую энергию формируют зоны МО. Как видно из рис.10.3 и 10.4 зоны 3s и 3р накладываются друг на друга, образуя единую зону, имеющую 4N орбиталей (N орбиталей s-зоны и 3N орбиталей р-зоны).
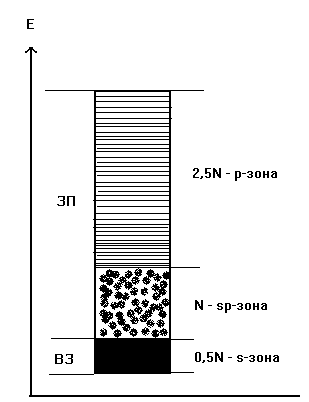
Рис. 10.4 - Энергетические зоны кристалла натрия при равновесном расстоянии атомов в кристаллической решётке.
Как видно из рис.10.4, валентной зоной в кристалле натрия является половина МО орбиталей s-зоны, имеющих минимальную энергию. Это связано с тем, что N атомов натрия, входящих в состав кристалла, имеют N электронов, расположенных в исходном состоянии на 3s АО, число которых также равно N. Из орбиталей типа 3s формируются N молекулярных орбиталей s-зоны. Так как в соответствии с принципом Паули на каждой МО могут располагаться по два электрона, N/2 наиболее низких орбиталей этой зоны будут заполнены электронами при 0оК, т.е. эти МО образуют валентную зону. Зона проводимости в данном случае будет представлять собой совокупность оставшихся орбиталей s-зоны и все орбитали р-зоны.
У атомов элементов главной подгруппы II группы на внешних ns – орбиталях по два электрона и, если бы р-зона не перекрывалась бы с s-зоной (рис. 10.3, 10.4, 10.5), последняя оказалась бы полностью заполненной и кристалл не имел бы выигрыша по энергии по сравнению с изолированными атомами. На рис. 10.5 видно, что 2N электронов атомов бериллия (при равновесном межатомном расстоянии d0) заполняют нижние орбитали s- и p-зон. Общее число занятых при 0оК МО орбиталей равно N, валентная зона являются sp-зоной, а зона проводимости представляет собой совокупность орбиталей верхней части sp- и р-зон.
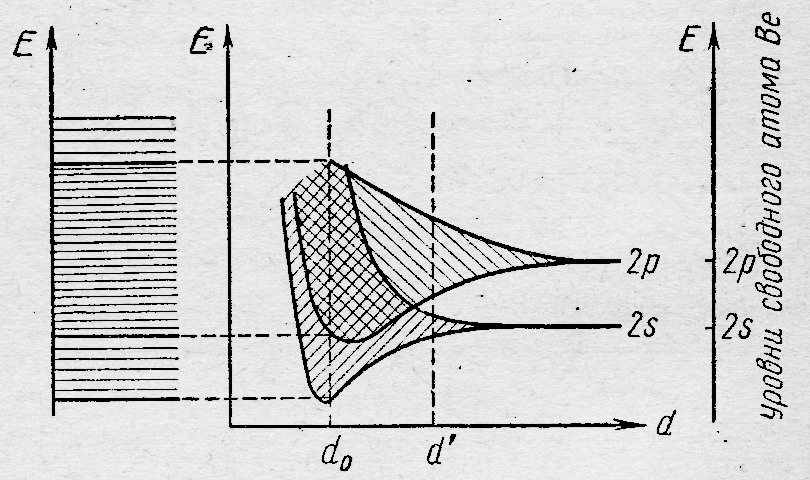
Рис.10.5 - Расположение энергетических зон в кристалле бериллия
d0– межатомное расстояние в кристалле бериллия
Из того же рисунка следует, что если бы расстояние между атомами бериллия было бы больше, чем d0 (например d1), то простоё вещество этого элемента относилось бы к полупроводникам. Аналогично кристаллу бериллия происходит заполнение МО орбиталей sp-зон в кристаллах магния и алюминия (в последнем случае электроны при 0оК занимают 1,5N МО орбиталей, имеющих минимальную энергию ).
У атомов элементов IV – VII периодов имеется шесть близких по энергии орбиталей, пять из которых принадлежат предвнешнему d-подуровню и одна внешнему s-подуровню. При взаимодействии N таких атомов образуется единая sd- зона, состоящая из 6N МО (рис.10.6). За счёт большего числа МО ширина этой зоны больше, чем зон, образующихся за счёт s и p-орбиталей (рис. 10.6 (а) и (б)). Так как энергия валентных электронов в кристалле кальция (при равном числе этих электронов) ниже, чем в кристалле магния, первый имеет более высокую энергию кристаллической решётки и более высокую температуру плавления.

Рис. 10.6 - Расположение энергетических зон в кристаллах: (а) кальция и (б) магния
Анализируя представленную выше теоретическую концепцию, можно сделать вывод, что с её помощью можно описывать химическую связь в любых кристаллических веществах. На рис.10.7 представлена схема формирования энергетических зон в кристалле алмаза. У атомов углерода, из которых он образован, валентными являются 2s и 2p орбитали. Из этих АО на первом этапе (d > d2), образуются две различные зоны (N МО s-зоны и 3N р-зоны). При дальнейшем сближении атомов в кристаллической решётке (d1< d <d2) исходные зоны сливаются в единую sp-зону состоящую из 4N МО. При (d < d1) единая энергетическая зона расщепляется на две зоны, каждая из которых состоит из 2N МО. Все 4N валентных электронов N атомов углерода (при равновесном межатомном расстоянии d0) располагаются на орбиталях нижней зоны, заполняя их полностью, а 2N орбиталей верхней зоны остаются свободными. Валентная зона и зона проводимости разделены запрещённой зоной, ширина которой (∆Е) для кристалла алмаза составляет 5,6 эВ, т.е. данный кристалл является диэлектриком.
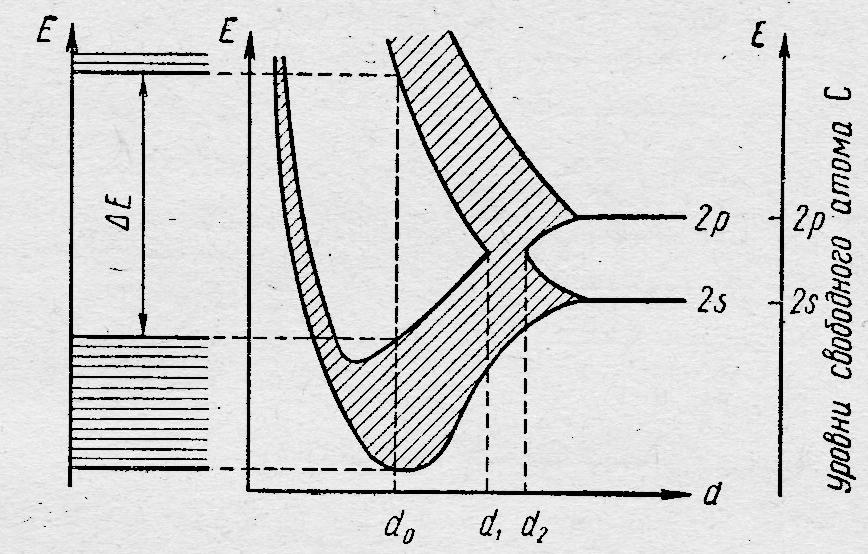
Рис. 10.7 - Расположение энергетических зон в кристалле алмаза.
d0– межатомное расстояние в кристалле алмаза.
Аналогичная картина образования энергетических зон наблюдается в кристаллах других простых веществ элементов главной подгруппы IV группы: кремния, германия и α-олова. С ростом радиуса атома длина связи между ними в кристаллах возрастает (d0 смещается в сторону d1), что приводит к уменьшению ∆Е : эта величина составляет для кремния 1,1 эВ, для германия 0,7 эВ и для α-олова 0,1 эВ, т.е. все они относятся к полупроводникам.
Использование зонной теории для описания ионных кристаллов рассмотрим на примере NaCl (рис.10.8). Как видно из данного рисунка МО орбитали в этом кристалле формируются из 3s АО атомов натрия и 3р АО атомов хлора. В исходном состоянии орбитали 3s атомов натрия расположены по энергии ниже 3р орбиталей атомов хлора. При сближении атомов происходит их ионизация с образованием катиона Na+ и аниона Cl־. Ион Cl־ оказывается в окружении положительно заряженных ионов Na+, что приводит к резкому снижению энергии электронов аниона. Наоборот, ион Na+ попадает в окружение анионов, отрицательный заряд которых приводит к росту энергии МО, сформированных из 3s АО. Нижняя р-зона содержит 3N МО, а N ионов Cl־ имеют 6N электронов на р-орбиталях. Следовательно в кристалле NaCl р-зона полностью заполнена и является валентной, а s-зона представляет собой зону проводимости и при 0оК полностью свободна.
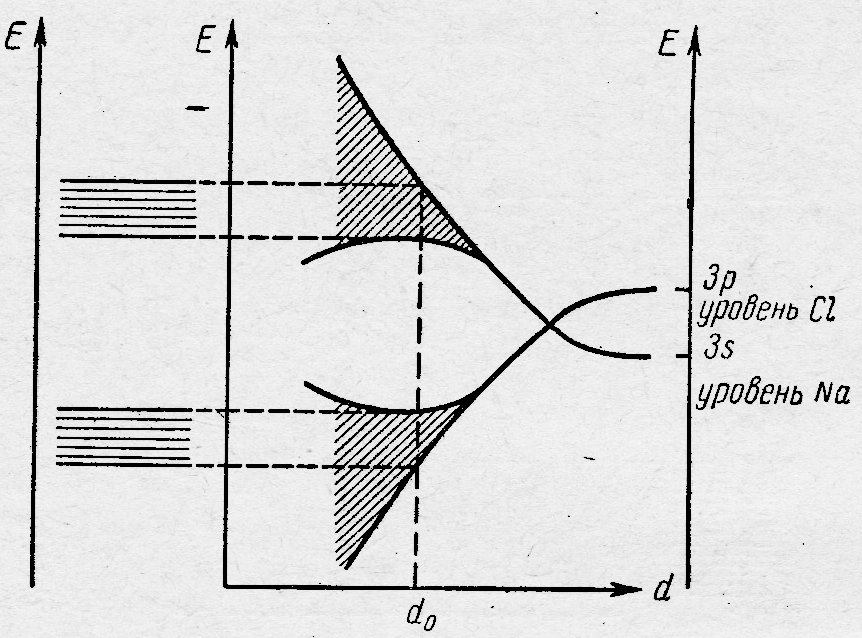
Рис.10.8 - Расположение энергетических зон в кристалле хлорида натрия.
d0– межионное расстояние в кристалле хлорида натрия.
Валентная зона и зона проводимости в кристалле NaCl разделены широкой запрещённой зоной (∆Е = 6 эВ), т.е. кристалл относится к диэлектрикам.
Рассмотренные примеры показывают, что строго говоря, деление кристаллов на проводники, полупроводники и диэлектрики условно. Так, например, если к кристаллу алмаза или NaCl приложить достаточное (определяемое значением ∆Е) напряжение, то электроны из валентной зоны перейдут в зону проводимости, т.е. кристалл будет проводить электрический ток. Напряжённость внешнего электрического поля достаточная для превращения диэлектрика в проводник называется напряжением пробоя. Очевидно, что чем больше значение ∆Е кристалла, тем при более высокой напряжённости внешнего поля наступает его пробой. То же касается теоретически возможного перехода проводник – полупроводник, рассмотренного выше на примере кристалла бериллия. Ещё больше стираются эти различия при высоких температурах, когда вероятность перехода электронов из валентной зоны в зону проводимости у диэлектриков и полупроводников резко возрастает, а электропроводность металлов наоборот снижается. Тем не менее в настоящее время принято считать, что если при с.у. кристалл имеет ∆Е > 3 эВ, то он относиться к диэлектрикам (монокристаллические и поликристаллические материалы на основе таких фаз называются изоляторами), если у кристалла при с.у. 0,1≤ ∆Е ≤ 3 эВ, то его относят к полупроводникам. В металлах ∆Е = 0, и они отличаются от полупроводников и диэлектриков обратно пропорциональной зависимостью электропроводности от температуры.
