
- •Федеральное государственное образовательное учреждение высшего профессионального образования
- •А. А. Нестеров, э.А.Бикяшев теория химического строения и свойства веществ
- •Модуль №1
- •1 Развитие представлений о строении атома
- •Ранние модели строения атома
- •1.2 Квантово-механическое описание атомов
- •1.3 Правила квантования
- •1.4 Правила заполнение электронами атомных орбиталей
- •1.5 Электронное строение атомов в основном состоянии. Связь электронного строения атомов и структуры периодической системы элементов
- •1.6 Закономерности изменения атомных (ионных) радиусов
- •1.7 Закономерности изменения энергий (потенциалов) ионизации
- •1.8 Закономерности изменения сродства к электрону
- •1.9 Электроотрицательности атомов и закономерности их изменения
- •Модуль №2 Электростатические представления в теориях химической связи
- •2.1. Теория электрохимического дуализма
- •2.2. Теория валентности
- •2.3. Теория ионной связи
- •2.3.1. Основные положения теории ионной связи Косселя
- •2.3.2.Оценка энергии ионной связи.
- •2.3.3. Границы применимости теории ионной связи
- •2.3.4 Энергия кристаллической ионной решетки.
- •2.3.5. Ионные радиусы
- •2.3.6. Ионные структуры
- •2.3.6.1. Основные принципы модели жесткой сферы
- •2.3.6.2. Границы применимости модели жесткой сферы
- •2.3.7. Основные свойства ионной связи и её недостатки
- •2.4. Теория поляризации.
- •2.5. Межмолекулярное взаимодействие.
- •Модуль №3
- •3.1. Теория Льюиса и метод олэп.
- •3.2.Основные принципы описания молекул в квантовой химии и метод валентных связей (мвс).
- •3.2.1. Основные принципы описания молекул в квантовой химии
- •3.2.2.Описание механизмов образования химических связей в рамках мвс
- •3.2.3. Описание строения молекул в рамках мвс
- •3.2.5. Дипольный момент и полярность связей
- •3.2.6. Достоинства и недостатки мвс
- •3.3. Метод молекулярных орбиталей (ммо).
- •3.4. Cравнение мвс и ммо
- •Модуль №4 Теория связи в металлах и комплексных соединениях
- •4.1. Химическая связь в кристаллах металлов.
- •4.1.1 Теория «электронного газа».
- •4.2 Зонная теория химической связи для кристаллов металлов, полупроводников и диэлектриков.
- •4.3 Строение кристаллов металлов.
- •4.4 Координационная теория а.Вернера, современная трактовка ее основных понятий и положений
- •4.4.1 Предпосылки создания теории строения комплексов
- •4.4.2 Координационная теория а.Вернера: состав комплексов, поведение в растворах, структура (изомерия)
- •4.4.3 Современная трактовка основных понятий координационной теории
- •4.4.4 Номенклатура комплексных соединений
- •4.4.5 Классификация комплексных соединений
- •4.4.6 Изомерия комплексов
- •4.4.7 Некоторые типы реакций с участием комплексных соединений
- •4.5 Теории химической связи в комплексах
- •4.5.1 Электростатическая (ионная) теория
- •4.5.2 Квантово-механические теории описания химической связи в комплексах
- •4.5.2.1 Метод валентных связей
- •4.5.2.2 Теория кристаллического поля
- •4.5.2.3 Варианты проявления энергетического расщепления орбиталей
- •4.5.2.4 Недостатки ткп
- •4.5.3 Теория поля лигандов (метод молекулярных орбиталей)
- •Заключение
- •Оглавление
1.2 Квантово-механическое описание атомов
Современная теория строения атомов стала развиваться после того, как вначале (в работах М.Планка, 1900г., и А.Эйнштейна, 1905г.) была доказана двойственная корпускулярно-волновая природа света (корпускула – частица). На этих идеях основаны модели Н.Бора (1913г.) и Бора-Зоммерфельда (1915г.). Но качественно новое представление об устройстве атомов, не отрицающее законы классической механики и электродинамики, а опирающееся на понимание ограниченности их применимости к микрообъектам стало возможным после того, как Луи де Бройль высказал предположение (1924г.), что дуализм следует приписать не только излучению, но и телам. Причем из предложенной формулы
λ = h / m · υ (1.21)
где λ – длина волны, соответствующая частице с массой m, движущейся со скоростью υ.
вытекало, что при уменьшении массы тела волновое поведение становится все более заметным (длина волны становится соизмеримой и даже может заметно превышать размеры частицы). Вскоре волновые свойства электронов были экспериментально обнаружены в опытах К.Дэвиссона и Л.Джермера (1927г.). При отражении потока электронов с энергией 1.6·10-17Дж от поверхности никеля была получена дифракционная картина в точности соответствующая той, что наблюдается, если заменить поток электронов на рентгеновское облучение такой же энергии. Но еще до этих опытов были опубликованы работы В.Гейзенберга (1925г.) и Э.Шредингера (1926г.), в которых формулировались важнейшие положения квантовой (волновой) механики и закладывались основы новой теории строения атома. Впоследствии было показано, что оба предложенных варианта приводят к тождественным результатам. Метод Э.Шрендингера оказался более удобным для выполнения расчетов. Поэтому современная теория строения атомов и теории химической связи основываются на этом методе. Но именно В.Гейзенбергу принадлежит приоритет в строгом обосновании вывода о том, что приписывать электронам в атомах конкретные траектории движения (орбиты) бессмысленно. Анализируя схему экспериментов по изучению траектории движения электрона, он доказал, что принципиально невозможно с высокой точностью одновременно определить координату и скорость его перемещения (принцип неопределенности Гейзенберга). В полученном В.Гейзенбергом выражении
Δх · Δυх ≥ ћ / m (1.22)
Δх – погрешность (неопределенность) в значении координаты частицы вдоль оси х, Δυх – погрешность (неопределенность) в составляющей значения скорости в том же направлении.
Соответственно, чем точней мы пытаемся определить координату (чем меньше Δх)
Δυх ≥ ћ / m·Δх , (1.23)
тем больше будет ошибка в определении скорости тела, особенно микрочастицы (масса, как Δх находятся в знаменателе дроби). Получается, что большие значения скоростей микрочастиц мы будем находить с большими погрешностями. Такие расчеты теряют смысл. То же самое относится и к попыткам точно рассчитать координату при заранее заданной высокой точности определения скорости. Например, рассчитанная по формулам Н.Бора скорость движения электрона на первой орбите составляет примерно 2181км/с. Округлим этот результат и представим его с точностью до десятков: ~2180 км/с. Очевидно, что такое округление выглядит оправданным. При этом мы позволили себе неточность в определении скорости Δυ ≈ 1км/с. Если теперь рассчитать по уравнению В.Гейзенберга с какой погрешностью мы в состоянии контролировать местоположение электроны, то получим Δх ≥ 1.16·103 Ǻ, что примерно в 2000 раз превышает размер атома водорода в основном состоянии (rН ≈ 0.53 Å). В то же время, чтобы гарантировать точность в определении координаты электрона ±0.001 Å (Δх = 0.002 Å) мы должны смириться с тем, что точность определения скорости не будет превышать ± ~289 407км/с (Δυ ≈ 578814км/с, что примерно в 265 раз больше найденного ранее значения).
Вывод: на законах классической механики построить правдоподобную теорию движения микрочастиц нельзя.
Энергетические состояния электронов не только в атоме водорода, но и в многоэлектронных атомах удалось описать, применяя не законы движения тел (при этом, накладывая на них необоснованные ограничения, что имело место в модели Н.Бора), а волновые законы. Волновое уравнение, предложенное Э.Шредингером для описания движения электрона в атоме, – уравнение объемной (атом трехмерен) стоячей волны (электрон его самопроизвольно не покидает и в стационарном состоянии не меняет своего поведения). Обсуждение вида этого уравнения, анализ вариантов его решения выходят за рамки данного пособия. Вкратце лишь отметим, что решением волнового уравнения является набор волновых функций Ψ (читается – пси). Причем для стационарного состояния Ψ является функцией координат (имеет разные значения в разных точках атома) и некоторых целочисленных коэффициентов (трех типов квантовых чисел):
Ψ = f (x,y,z; n,m,l). (1.24)
Аналитический вид волновых функций мы также обсуждать не будем. Но с некоторыми качественными моментами необходимо познакомиться. Так вот, значение волновой функции Ψ в каждой точке имеет смысл амплитуды электронной стоячей волны. Этим словам не очень легко найти аналогию в привычном для нас макромире. А вот ее квадрат, или, строго говоря,
произведение Ψ2·dV соответствует вероятности пребывания электрона в микрообъеме (точке) атома с координатами x+dx, y+dy, z+dz.
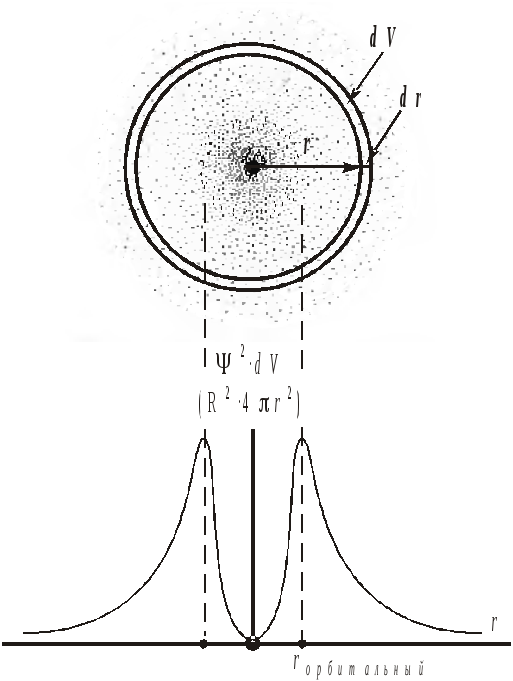
|
Рис. 1.6 – Схематичное изображение электронного облака атома водорода и его вероятностное описание. |
