3. Объединение и пересечение множеств, их свойства

_____________________________________________________________

Определение 5. Объединением двух множеств А и В называется множество, состоящее из элементов, которые принадлежат, хотя бы одному из этих множеств.

_____________________________________________________________________________________

Объединение множеств А и В обозначают А В, где символ  знак объединения множеств, А В = {х/х  А или х В}.

Например, А = {1,2,3,4}, В = (3,4,5,6},АВ={1,2,3,4,5,6}.

На диаграмме Эйлера-Венна заштриховано объединение множествА и В.

Очевидно, чтохАВ тогда и только тогда, когда х  А и х  В. Операция объединения множеств обладает следующими свойствами:

1. Для любых множеств А и В имеем:

А  В = В  А (коммутативность).

2. Для любых множеств А, В и С имеем:

(А  В)  С = А  (В  С) = А  В  С (ассоциативность).

3. Если В А, то А В = А.

В частности, для любого множества А имеем:

А А=А; А=А; АИИ.

Проиллюстрируем некоторые свойства с помощью диаграмм Эйлера:

И

Заштриховано объединение множеств А  В и А  И

____________________________________________________________

Определение 6. Пересечением множеств А и В называют множес­тво, состоящее из всех тех и только тех элементов, которые одно­временно принадлежат и множеству А, и множеству В.

____________________________________________________________________________________

Пересечение множеств А и В записывают А  В, где  - знак пере­сечения множеств.

А  В = {х/х  А и х  В}.

Например: А = {1,2, 3,4}; 5= {3,4, 5, 6}; А  В = {3,4}.

На диаграмме Эйлера-Венна заштриховано пересечение множеств А и В.

Очевидно, что х  А  В тогда и только тогда, когда х  А или х  В.

Операция пересечения множеств обладает следующими сво­йствами:

1. Для любых множеств А и В имеем:

А  В = В  А (коммутативность).

2. Для любых множеств А, В и С имеем:

(АВ)  С = А  (ВС)=АВ  С (ассоциативность).

3. Если А  В ,то А  В = А.

В частности, для любого множества А имеем

А  А = А; А   =  ; А  И = А.

Проиллюстрируем третье свойство с помощью диаграмм Эйлера-Венна.

И

На рисунках заштриховано пересечение множеств А  В и А  И. Операции объединения и пересечения множеств связаны дистри­бутивными законами:

1. А  (В  С) = (А  В)  (А  С)- дистрибутивный закон пересече­ния относительно объединения слева;

2. А  (В  С) = (А  В)  (А и С) - дистрибутивный закон объединения относительно пересечения слева.

4. Разность множеств. Дополнение к подмножеству

_______________________________________________________________

Определение 7. Разностью множеств А и В называется мно­жество, состоящее из тех и только тех элементов, которые принадлежат множеству А, но не принадлежат множеству В.

_________________________________________________________________________________________

Операция нахождения разности двух множеств называется вычитанием множеств.

Разность множеств А и В обозначают символом А\В. Таким обра­зом, по определению, А\В = {х/х  А и х  В}.

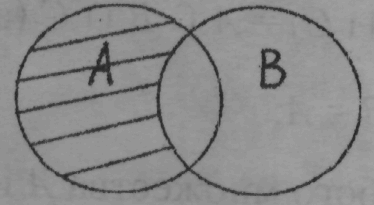
На рисунке А\В заштриховано.

Например, А = {1, 2, 3, 4}; В = {3, 4, 5, 6},

А\В = {х/х  А и х  В} = {1,2},

В\А= {х/х  В и х  А} = {5,6}.

Очевидно, что х  А\В тогда и только тогда, когда х  А или х  (А  В).

Для любых множеств А, В и С справедливы следующие раве­нства, связывающие вычитание множеств с другими операциями над множествами:

а) А\(В  С) = (А\В)  (А\С);

б) А\(В  С)= (А\В)  (А\С).

____________________________________________________________

Определение 8. Если В подмножество А, то разность А\В назы­вают дополнением к подмножеству В и обозначают В'_А.

_________________________________________________________________________________________

Таким образом, В  А, А\В = В'_А .

На рисунке множество В'_А заштриховано.

Так, если А – множество учащихся в некотором классе, а В – мно­жество девочек в нем, то В'_А есть множество мальчиков в этом классе.

Если для множеств А, В, ... фиксировано некоторое универсаль­ное множество И, то вместо А'_и , В'_и пишут А', В',...

Очевидно, что х  А', тогда и только тогда, когда х  А или х  И.

Для любых подмножеств А и В универсального множества И име­ют место следующие равенства:

1. (А  В)' = А'  В'

2. (А  В) ' = А'  В'

Задача 1

1. Множество А – множество натуральных делителей числа 6. За­дать множество: а) перечислением элементов, б) графически, в) с по­мощью характеристического свойства.

2. Изобразить множество В = {х/х  R, 1  х < 3, 5} на числовой прямой.

Решение.

1. Множество А задано словесно – множество натуральных дели­телей числа 6, т.е. множество натуральных чисел, на которые число 6 делится без остатка (6 х).

а) А = {1, 2, 3, 6};

б)

в) А = {х/х  N, 6 х } .

2. Множество В задано с помощью характеристического свойства. Перейти к заданию множества В в виде промежутка и изобразить на числовой прямой.

В ={х/хR,1 х < 3,5} = [1; 3,5)

Задача 2.

Проиллюстрируйте с помощью диаграмм Эйлера высказывания:

а) некоторые нечетные натуральные числа кратны 5;

б) все студенты нашего курса присутствовали на лекции по математике.

Решение.

Выделим множества, о которых идет речь в данных высказываниях:

а) пусть А – множество нечетных натуральных чисел, В – множество натуральных чисел, кратных 5.

В данном высказывании говорится, что некоторые элементы множества А являются и элементами множества В (например, 5, 15), т.е. множества А и В имеют общие элементы. Но в каждом множестве есть элементы, не принадлежащие другому.

Поэтому круги для множеств А и В надо изобразить так, чтобы они пересекались друг с другом (рис. 4).

Рис.4 Рис.5

б) Пусть D – множество студентов курса, C – множество студен­тов, присутствовавших на лекции по математике.

В данном высказывании утверждается, что каждый элемент мно­жества С является и элементом множества Д (все элементы множес­тва С принадлежат множеству Д). По определению отношения вклю­чения, это означает, что С  Д. Поэтому круг для множества С распо­ложен внутри круга для множества Д (рис. 5).