Свойства операции сложения

Имеют место следующие теоремы:

(записаны в таком порядке, в каком их можно доказать).

Для любых а, b, с из N

1. (а + b) + с = а + (b + с) = а + b + с; (ассоциативность)

2. а + b =b + а; (коммутативность)

От перемены мест слагаемых сумма не меняется.

3. а + b  bа + b а;

Сумма двух любых натуральных чисел не равна ни одному из слагаемых.

4. а + b > аа + b >b;

Сумма двух любых натуральных чисел больше любого из этих чисел.

5. а = b => а + с = b + с;

6. а + с = b + с =>а =b;

а + b = а + с => b = с. (сократимость)

7. а < b => а + с < b + с;

8. а + с < b + с => а < b;

а + b < а + с => b < с; (монотонность)

9. а >b => а + с >b + с;

10. а + с > b + с => а > b;

а + b > а + с => b > с; (монотонность)

Свойства операции умножения

Имеют место следующие теоремы: (записаны в таком порядке, в каком их можно доказать). Для любых а, b, с из N:

1. (a + b)  c = ab + ac

(дистрибутивность справа относительно сложения)

1. а  (b + с) = аb + ас

(дистрибутивность слева относительно сложения)

3. (аb) с = а(bс) = аbс; (ассоциативность)

4. аb = bа; (коммутативность)

5. а=b => ас=bс;

6. ас = bс => а = b;

аb = ас => b = с; (сократимость)

7. а < b => ас<bс;

8. ас<bс => а < b;

9. а>b => ас >bс;

10. ас >bс => а > b

11. (а,b )(n )nb >а.

___________________________________________________________________

Определение 5. Число а меньше числа b(а < b) тогда и только тогда, когда существует такое натуральное число с, что а + с = b.

______________________________________________________________________________________________

При этих условиях говорят также, что число b больше а, и пишут: b > а.

Символически это определение можно записать так: а < b  (с )а + с = b или b > а  (с )а + с = b.

Например:

1. 7 < 9, т.к. существует число с = 2, такое, что 7 + 2 = 9.

2. 5 > 2, т.к. существует число с = 3, такое, что 2 + 3 = 5.

Задача 3.

Доказать свойство ассоциативности операции сложения, т.е. (а,b,c )(а + b) + с = а + (b + с).

Решение.

Будем пользоваться аксиомой индукции A₄.

Пусть натуральные числа а и b выбраны произвольно, а с принимает различные натуральные значения (индукция по с).

Обозначим через М множество всех тех и только тех натуральных чисел с, для которых равенство (а + b) + с = а + (b + с) верно.

M = {с\с N, (а + b) + с = а + (b + с)}; т.к. с  N , то М  N.

1. Докажем сначала, что 1  M, т.е. убедимся в справедливости ра­венства (а + b) + 1 = а + (b + 1). Действительно, по определению сложения, имеем (а + b) + 1 (а + b)' а + b' a + (b + 1), что и требовалось доказать (ч.т.д.) => 1  M.

2. Докажем теперь, что если сM => с' M . Пусть с  M (это предположение индукции – П.И.), т.е. равенство

(a + b) + c = а + (b + с) верно, докажем, что с' M, т.е. равенство (а +b) + с' = а + (b + с') верно. Верность числовых равенств можно доказать одним из следующих приемов:

• взять левую часть равенства, путем преобразований получить правую часть равенства;

• взять правую часть равенства, путем преобразования получить левую часть равенства;

• преобразовывая левую и правую части равенства, получить одинаковые числовые выражения.

Будем преобразовывать левую часть равенства.

(а + b) + с' ((а +b) + с)' (а + (b + с)) ' а + (b + с)' а +(b + с') ч.т.д. => с'  M.

Итак, мы показали, что

M  N  (1 M (с  M  с' M)) => М = N, т. е. равенство (а + b) + с = а + (b + с) истинно для любого натурального числа с, а т.к. а и b выбирались произвольно, то оно справедливо для любых натуральных чисел а и b, что и требовалось до­казать.

Задача 4.

Доказать дистрибутивность слева умножения относительно сложения, т.е.

(а,b,с N) а(b + с) = аb + ас.

Доказательство:

Пусть натуральные числа а и b выбраны произвольно, а с принимает различные натуральные значения (индукция по с).

Обозначим через М множество всех тех и только тех натуральных чисел с, для которых равенство а(b + с) = аb + ас верно, т.е.

М = {ссN, а(b + с) = аb + ас}, т.к. с  N, то М  N,

I. Докажем, что 1  М, т.е. а  (b + 1) = аb + а 1.

ab',

а  b + а  1 а b + а аb',

получили аb' = аb' – истинно, => 1  М.

II. Докажем, что с  М => с'  М

Пусть с  М, т.е. а(b + с) = аb +ас.

Докажем, что с' М, т.е. а(b + с') = аb + ас'.

Преобразуем левую часть равенства к правой части этого равенства.

а(b + с') а(b + с)' a(b + с) + а (аb + ас) + а аb + (ас + а) аb + ас'

ч.т.д., => с' М, тогда М  N(1 M (с  М => с'  М)) => M = N, т.е. равенство а(b + с) = аb+ас истинно для любого натурального числа с, а также для любых натуральных чисел а и b, т.к. они были выбраны произвольно.

Доказательство свойств операций сложения и умножения проводилось на основе аксиомы индукции Пеано (аксиома 4).

Его можно применять для доказательства других утверждений о натуральных числах, опираясь на следующую теорему.

Теорема 5. (Принцип математической индукции).

Если утверждение А(n) с натуральной переменой n истинно – для n = 1, т.е. А(1) – истинно и из того, что оно истинно для n = к, т.е. А(к) – истинно (к – произвольное натуральное число), следует что оно истинно для следующего числа n=к¹, то утверждение А(n) истинно для любого натурального числа n.

(к¹= к+1)

Доказательство методом математической индукции состоит из двух частей:

1. Доказывают, что А(1) – истинно (n = 1)

2. (П.И.) Предполагают, что утверждение А(к) – истинно (n = k) и, используя это предположенив, доказывают, что А(к¹) – истинно (n = к¹ = к + 1), т.е.

А(к)  А(к¹) истинное высказывание.

Если А(1)  (А(к)  А(к¹)) – истинное высказывание, то делают вывод об истинности утверждения А(n) для n.

Задача 6. Доказать, что для любого натурального числа n, сумма n первых чисел натурального ряда S(n) = т.е. 1 + 2 + 3 + … +n =-S(n).

Решение.

1. При n = 1 утверждение истинно, т.к. в левой части равенства имеем

S(1)= 1, в правой

2. П.И. (предположение индукции). Пусть при n = к S(к) – истинно, т.е.

1 + 2 + 3 + … + к = . Докажем, что А(к) А(к+1) – истинно.

Действительно, S(к+1)= 1 + 2 + … + к + (к + 1) = S(к)+(к + 1). По предположению S(к)=,значит, S(к+1)=+(к+1)= =Таким образом, А(к)  А(к¹) – истинно.

Следовательно, на основании принципа М.И. данное утверждение S(n) – истинно для любого натурального n.

Задача. Докажем методом М.И., что утверждение (6ⁿ – 1) 5n.

1. Пусть n = 1; 6¹ – 1 = 5; 5:5 – истинно значит, при n = 1 утверждение истинно.

2. Допустим (П.И.), что при n = к утверждение (6^к – 1) 5 – истинно. Докажем, что оно будет истинным, при n = к + 1 = к¹, т.е. (6^k – 1) 5.

1 способ. Рассмотрим разность (6^к+1–1)–(6^к–1). После преобразований получаем: 6^к+1 – 1 – 6^к + 1 = 6^к  (6 - 1) = 6^к  5. Произведение (6^к  5)5, т.к. 55, а (6^к-1)5 (по предположению). Получаем 6^к+1 – 1 = (6^к – 1) + 6^к  5, т.к. каждое слагаемое делится на пять, то по теореме о делимости суммы (6^к+1 – 1) 5.

2 способ. Преобразуем выражение 6^к+1 – 1 = 6^к  6 – 1. Прибавим и вычтем число 6, получим 6^к+1 – 1 = 6^к  6 – 6 + 6 – 1 = 6(6^к – 1) + 5. В полученном выражении (6^к – 1) 5 по предположению, а т.к. второе слагаемое 5, то (6(6^к – 1) + 5) 5, а это значит (6^к+1 – 1) 5.

На основании доказанного и теоремы индукции утверждение (6ⁿ – 1) 5 при любом натуральном n.

Контрольные вопросы

1. Сформулируйте и запишите свойства операции сложения.

2. Используя определение сложения, найдите значение выражения:

а) 3 + 2; б) 3 + 3; в) 3 + 4;

3. Какие законы сложения изучаются в начальном курсе математики? Приведите примеры.

4. Объясните, какие теоретические положения используются при нахождении суммы 6 + 3:

6 + 3 = 6 +(2 + 1) = (6+ 2)+1 = 8+1 = 9.

5. Используя определение умножения, найдите значение выражения:

а) 3  2; б) 3  3; в) 3  4.

6. Сформулируйте и запишите свойства операции умножения.

7. Какие законы умножения изучают в начальном курсе математики? Приведите примеры их использования.

8. Дайте определение отношения «меньше» («больше») для натуральных чисел.

9. Какое из отношений:

а) отношение «меньше»;

б) отношение «больше»;

в) отношение «непосредственно следовать за»является отношением порядка?

10. Запишите законы монотонности сложения и умножения натуральных чисел. Какие свойства неравенств они выражают?

11. Сформулировать принцип математической индукции.

Упражнения

289. Доказать коммутативный закон сложения натуральных чисел.

290. Составить таблицу прибавления 3 со всеми теоретическими обоснованиями.

291. Доказать, что для любых натуральных чисел а и b верны утверждения:

a) а +b  b

б) а +b  a  a + b  b

292. Доказать, что для любых натуральных чисел а, b и с верны утверждения:

a) а= b => а + с = b + с;

б) а + b= а + с => b = с;

в) а = b => ас = bс;

г) ас = bс => а = b;

д) аb = ас => b = с.

293. Составить таблицу прибавления 4 со всеми теоретическими обоснованиями.

294. Докажите, что для любых натуральных чисел а, b и с верны утверждения:

а) а< b => а + с < b + с;

б) а + с < b + с => а < b;

в) а + b < а + с => b < с;

г) а > b => а + с > b + с;

д) а + с > b + с => а > b;

е) а + b > a + с => b > c.

295. Составить таблицу прибавления 5 и 6 со всеми теоретическими обоснованиями.

296. Составить таблицу прибавления 7,8 и 9 со всеми теоретическими обоснованиями.

297. Применяя законы сложения вычислить результат; каждый случай применения законов объяснить:

а) 57689+ 48997+ 42311;

б)73562 + 3463 + 26438;

в) 3186+ 48763+ 6814;

г) 6747+17896+ 3253;

д) 42879+ (37999+ 57121).

298. Доказать дистрибутивность справа умножения относительно сложения.

299. Докажите, что для любых натуральных чисел а, b и с верны утверждения:

а) а < b => ас < bс;

б) ас < bс => а < b;

в) аb < ас => b < с;

г) а > b => ас > bс;

д) ас > bс => а > b;

е) аb > ас => b > с.

300. Доказать, что каждое из ниже указанных отношений, заданных на множестве натуральных чисел, является отношением порядка:

а) отношение «меньше»;

б) отношение «больше».

301. Доказать, что для любых натуральных чисел а и b существует такое натуральное число п, что пb > а. Привести примеры.

302. Используя определения отношений «меньше», «больше», докажите истинность следующих утверждений:

а) 5 < 7;

б) 6 > 3.

303. Используя теоретические положения, объясните истинности следующих утверждений:

а) 3 + 7 > 3 + 6;

б) 5 + 4 < 9 + 4;

в) 4 ∙ 7 > 4 ∙ 5;

г) 3 ∙ 6 < 5 ∙ 6;

д) 5 ∙ 7 < 7 ∙ 9;

е) 5 + 4>4 + 3;

ж) 7 ∙ 4 > 4 ∙ 3;

з) 3 + 6 < 6 + 5.

304. Какие теоретические положения неявно используют учащиеся при выполнении задания:

а) заполни пропуски так, чтобы получились верные равенства и неравенства:

9 ∙ 6 = 6 ∙ □; 8 ∙ 3 > 8 ∙ □; 78 + 18 < 78 + □.

б) верны ли следующие записи:

32 + 40 < 32; 27 + 30 > 27?

в) >; < ?

70 + 15  70 + 18; 14 + 46  12 + 46.

305.Какие свойства умножения могут быть использованы при нахождении значения выражения:

а) 5 ∙ (10 + 6);

б)125 ∙ 14 ∙ 5;

в) (8 ∙ 137) ∙ 125;

г) 48 ∙ 125?

306. Известно, что 37 ∙ 3 = 111. Используя это равенство, вычислите:

а) 37 ∙ 21; б) 185 ∙ 18.

307. Опираясь на коммутативные законы умножения и сложения, напишите выражения, равные (т + п) ∙ а.

308. Составить со всеми теоретическими обоснованиями таблицы умножения на числа:

а) 3; б) 4; в) 5; г) 6 и 7; д) 8 и 9.

309. Применяя законы умножения, вычислите результат:

а) 4 ∙ 5 ∙ 2 ∙ 25 ∙ 17;

б) 8 ∙ 7252 ∙ 125;

в) 7546 ∙ 5 ∙ 25 ∙ 4 ∙ 2;

г) 2 ∙ 3246 ∙ 5 ∙ 250 ∙ 4;

д) 4 ∙ 6524 ∙ 25.

310.Какие свойства умножения будут использовать учащиеся начальных классов, выполняя следующие задания:

1) Можно ли, не вычисляя, сказать, значения каких выражений будут одинаковы:

а) 2 ∙ 5 + 2 ∙ 3; б) 5 ∙ (3 + 2); в) (5 + 3) ∙ 2.

2) Верны ли равенства:

а) 19 ∙ 5 ∙ 2 = 19 ∙ (5 ∙ 2); в) 3 ∙ 5 + 8 ∙ 5 = (3 + 8) ∙ 5;

б) (4 ∙ 10) ∙ 13 ∙ 4 ∙ 10 ∙ 31; г) 7 ∙ (6 + 8) = 7 ∙ 6 + 8 ∙ 7.

3) Можно ли, не выполняя вычислений, сравнить значения выражений:

а) 60 ∙ 42 + 3 ∙ 42…63 ∙ 40 + 63 ∙ 2;

б) 59 ∙ 90 + 59 ∙ 5…50 ∙ 95 + 9 ∙ 95.

311. Не выполняя вычисления, вместо звездочки поставьте знак = или <, чтобы получилось истинное высказывание:

а) 354 + 246  354 + 246;

б) 273 + 475  237 + 456;

в) 271 + 543  271+ 537;

г) 237 + 425  273 + 425;

д) 546 ∙34  546-31;

е) 329 ∙ 78  329 ∙ 84;

ж) 513 ∙73  513 ∙ 73;

з) 275 ∙ 94  257 ∙ 94;

и) 25 ∙41 + 4 ∙ 41  20 ∙ 41 + 9 ∙ 41;

к) 73 ∙ 28 + 5 ∙ 29  20 ∙ 78 + 9 ∙ 78;

л) 53 ∙ 38 + 4 ∙ 38  30 ∙ 59 + 8 ∙ 59;

м) 32 ∙ 52 + 5 ∙ 52  50 ∙ 32 + 2 ∙ 32.

Доказать методом М.И. следующие предложения:

1. (8ⁿ + 6) : 7

2. 1 + 3 + 5 + … + (2n – 1) = n²

3. 1² + 2² + 3² + … + n² =

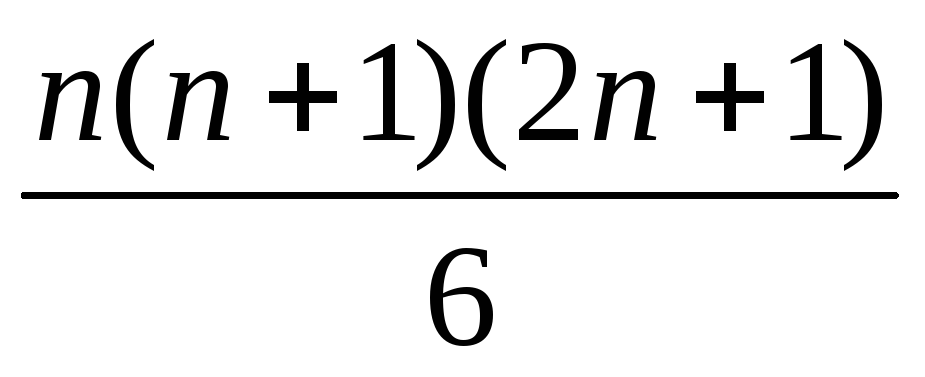
4. (n³ + 5n) : 6

5. (6^2n-1 + 1) : 7

6. (4ⁿ – 1) : 3

Дать теоретическое обоснование вашему выбору.

312. Сформулировать и дать теоретическое обоснование правил:

а) прибавления числа к сумме;

б) прибавления суммы к числу;

в) прибавления суммы к сумме. Проиллюстрировать примерами.