Деление суммы на число

Теорема 9. Если числа а и b делятся на число с, то их сумма а + b делится на с, причем частное, получаемое при делении суммы а + b на число с, равно сумме частных получаемых при делении а на с и b на с, т.е. (а + b):с = а:с + b:с.

Например, (60 + 16): 2 = 60 : 2 + 16 : 2 = 38. Эту теорему можно сформулировать в виде правила: для того чтобы разделить сумму на число, достаточно разделить на это число каждое из слагаемых и полученные результату сложить.

Деление разности на число

Теорема 10. Если натуральные числа а и b делятся на число с и а > b, то разность а – b делится на с, причем частное, получаемое при делении разности на число с, равно разности частных, получаемых при делении а на с и b на с, т.е. (а – b): с = а : с – b : с.

Например, (36 – 27) : 3 = 36 : 3 – 27 : 3 = 12 – 9 = 3.

Эту теорему можно сформулировать в виде правила:

для того чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе.

Деление произведения на число

Теорема 11. Если натуральное число а делится на натуральное число с, то для любого натурального числа b произведение аb делится на с. При этом частное, получаемое при делении произведения аb на число с, равно произведению частного, получаемого при делении а на с, т.е. (а  b): с = (а : с)  b.

Например (6  115) : 3 = (6 : 3)  115 = 230. Теорему можно сформулировать в виде правила: для того чтобы разделить произведение на число, достаточно разделить на это число один из множителей и полученный резуль­тат умножить на второй множитель.

Задача 7.

Доказать дистрибутивность слева умножения относительно вы­читания, т.е.

(а, b,с N) a(b – с) = аb - ас (если b > с).

Доказательство:

Будем использовать определение разности натуральных чисел. Покажем, что если к вычитаемому ас прибавим разность а(b - с), то получим уменьшаемое аb.

, ч.т.д.

Задача 8.

Доказать, что если разность натуральных чисел а и b существует, то она единственна.

Доказательство:

Доказывать будем методом от противного. Предположим, что существует два различных значения разности чисел а и b: а – b = с₁ и а – b = с₂, причем c₁  с₂.

Тогда, по определению разности, имеем а = b + с₁ и а = b + c₂ . Отсюда следует, что b + c₁ = b + c₂ (по транзитивности отношения «равно»).

По свойству сократимости операции сложения получим, что с₁ = с₂. Пришли к противоречию с допущением, значит оно не верно, а верно данное утверждение (теорема о единственности разности).

Задача 9.

Пусть а, b, с – натуральные числа.

Доказать, что (а + b) – с = (а - с) + b, если а > с.

Доказательство:

По определению разности, если к вычитаемому с прибавим разность ((а – с) + b), то должны получить уменьшаемое а + b.

, ч.т.д.

Задача 10.

Пусть а, b, с – натуральные числа и а > b + с. Доказать, что а – (b + с) = (а– с) – b.

Доказательство:

По определению разности, если к вычитаемому (b + с) прибавим разность ((а – с) – b), то должны получить уменьшаемое а.

, ч.т.д.

Задача 11.

Пусть а, b, с – натуральные числа.

Доказать, что если а и b делятся на с, то (а + b): с = а : с + b: c

Доказательство:

По определению частного, если делитель с умножим на частное (a:с + b:с), то должны получить делимое (а + b).

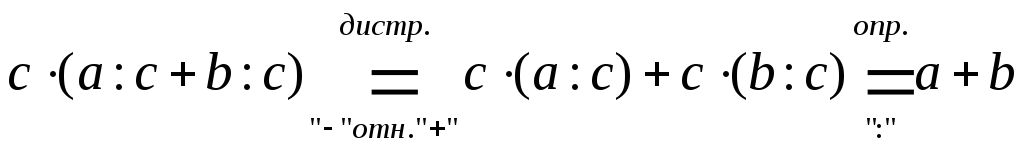, ч.т.д.

Задача 12.

Доказать, что для того, чтобы существовало частное двух нату­ральных чисел а и b, необходимо, чтобы b  а.

Доказательство:

Надо доказать, что (а : b) -  => b  а, где а, b N.

Пусть (а: b) существует, тогда, по определению частного, (с  N) а= b с. Т.к. с  N, то (с  N) 1  с. Умножим обе части неравенства на b, получаем b с. Но bс = а, следовательно, b  а.

Задача 13.

Пусть а, b, с – натуральные числа и число а делится на число b.

Доказать (с  N)а : b = ас : bс, т.е. частное не меняется, если де­лимое и делитель умножить или разделить на одно и то же натураль­ное число.

Доказательство: Пусть ас : bс = х, т.е.,

, ч.т.д.

Например: 375 : 15 = (375  2) : (15  2) = 750 : 30 = 25.

Задача 14.

Пусть а, b, с – натуральные числа, тогда а: (bс) = (а:b):с, если де­ление выполнимо, то деление на произведение можно осуществить делением а на отдельные множители.

Пусть

Контрольные вопросы

1. Сформулировать и записать в символической форме определение разности натуральных чисел.

2. Доказать, пользуясь определением разности натуральных чисел, что:

а) 7 – 4 = 3; б) 8 – 5  2; в) (5 – 9) – не существует в N.

3. Сформулировать теоремы об условии существования и единственности разности натуральных чисел.

4. Как можно вычесть число из суммы? Проиллюстрировать примерами.

5. Как можно вычесть сумму из числа? Проиллюстрировать примерами.

6. Доказать истинность утверждений: (а + b) – а = b; ( а + b) – b = а.

7. Сформулировать и записать в символической форме определение частного натуральных чисел.

8. Доказать, пользуясь определением частного натуральных чисел, что

а) 42 : 7 = 6; б) 40 : 8  3; в) (35 : 4) – не существует в N.

9. Сформулировать теорему об условии существования частного натуральных чисел. Почему это условие является только необходимым?

10. Сформулировать теорему о единственности частного.

11. Сформулировать правила деления суммы, разности и произведения натуральных чисел на натуральное число. Проиллюстрировать эти правила примерами.

Упражнения

313. Сформулируйте условие существования разности во множестве натуральных чисел и докажите его.

314. Доказать, что при b < а и любых натуральных с верно равенство (а – b)с – ас – bс.

315. Докажите, что:

а) если b > с, то (а + b) - с = а + (b - с);

б) если а > b + с, то а - (b + с) = (а – b) – с.

316. Докажите, что b – а < b.

317.Что является теоретической основой следующих приемов вычислений, изучаемых в начальном курсе математики:

а) 13 –7

13–3–4 13 – 7 = 6;

б) 15 – 8 = (8 + 7) – 8 = 7;

в) 26 – 9 = 26 – 6 – 3 = 17;

г) 57 – 40 = (50 + 7) – 40 = 10 + 7=17;

д) 57 – 4 = (50 + 7) – 4 = 50 + 3 = 53;

е) 42 – 5 = 42 – (2 + 3) = 40 – 3 = 37.

318. Определите значение выражения, не выполняя письменных вычислений. Ответы обоснуйте.

а) 8536  7 – 8536  6;

б) 729  11 – 729;

в) 13  24 – 8  24;

г) 11  957 – 957.

319. Пусть а, b, с, d – натуральные числа и а > b, с >d. Доказать истин­ность следующих высказываний:

а) а – b = с – d а + d = b + с;

б) (а – b) –( с – d)=( а + d) –( b + с);

в) (а – b)(с – d)= (ас + bd) –(ad + bс);

320. Найдите разность, применяя приемы вычисления, используемые в начальной школе. Дать теоретическое обоснование приемам.

1) 13 – 4;

2) 15 – 6;

3) 30 – 8;

4) 40 – 7;

5) 52 – 30;

6) 74 – 20;

7) 40 – 36;

8) 50 – 47;

9) 64 – 3;

10) 79 – 5;

11) 80 – 32;

12) 60 – 24;

13) 65 – 8;

14) 73 – 6;

15) 89 – 85;

16) 77 – 72;

17) 76 – 55;

18) 47 – 35;

19) 72 – 56;

20) 84 – 38.

321. Можно ли, не выполняя вычислений, сказать, значения выражений будут равны:

а) (60 + 15) – 13;

б) (60 – 13) +15;

в) (60 – 13) – 15;

г) 60 + (15 – 13);

д) 60 – (15 – 13);

е) (60 +13) – 16;

ж) 60 – (15 + 13);

з) (60 – 15) +13;

и) (60 – 15) – 13;

к) (60 – 13) + 15;

л) (60 –13) –15;

м) 60 – 15 – 13.

322. Докажите, что:

а) если частное натуральных чисел а и b существует, то оно единственно;

б) если числа а и b делятся на с и а > b, то(а – b): с = а : с – b : с;

в) если число а делится на число с, то (bN) (а  b): с = (а : с)  b;

г) (b : с)а = (аb): с.

Дайте словесные формулировки этим утверждениям.

323. Можно ли считать, что все данные утверждения истинны. Ответ обосновать.

а) 75 : (3 5) = 75 : 3 : 5; б) 96 : (3  8) = 96 : 3 : 8; в) 910: 130 = 910 : 10: 13.

324. Доказать, что деление

а) неассоциативно;

б) некоммутативно.

325. Какие свойства деления являются теоретической основой выполнения следующих заданий, предлагаемых школьникам начальных классов? Можно ли, не выполняя деления, сказать, значения каких выражений будут одинаковы:

а) (30 + 6) : 3;

б) (21 + 15) : 3;

в) 36 : 2;

г) (11 +25) : 2;

д) (20 + 16) : 3;

е) 36 : 3.

326. Верны ли равенства:

а) 96 : 8 : 2 = 96 : (8 : 2);

б) 96 : 8 : 2 = 96 : (8  2);

в) 96 : 8 : 2 = (24 : 8)  (4 : 2);

г) (60 – 12) : 3 = 20 – 4.

327. Найдите значение выражения рациональным способом; свои действия обоснуйте:

а) (9  57) : 9;

б) (2 7 9) : 18;

в) (35  48) : (7  6);

г) (18  35) : 14;

д) (195 : 13)  2;

е) 720 : 48;

ж) 954 : 18;

з) 882 : 18;

и) 480 : 32;

к) (560  32) : 16.

328. Не выполняя деления уголком, найдите наиболее рациональным способом частное; выбранный способ обоснуйте:

а)540 : 15;

б)378 : 7;

в) 385 : 55;

г) 428 : 85;

д) 240: 15;

е) 455 : 65;

ж) 555: 15;

з) 665 : 35;

и) 567 : 27;

к)541 : 19;

329. Укажите условия, при которых следующие равенства истинны:

а) ( а + b): с = а : с + b : с;

б) (а – b) : с = а : с – b : с;

в) (а₁  а₂  ... a_n) : b = (а₁ : b)  (а₂ а₃ ...  а_n) = а₁  (а₂ : b)  (а₃  а₄  … а_n) = ...= а₁ а₂ ...  а_n-1 (а_n : b).

г) а : (b с) = (а : b) : с; а : (b  с) = (а : с): b;

д) а (b : с) = (а  b) : с; а  (b : с) = (а : с)  b;

е) а : (b : с) = (а : b)  с.