9.3.КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ

Уравнения перемещений при расчете статически неопредели­ мых систем методом сил записывают в определенной к а н о н и- ч е с к о й форме.

Если заданная статически неопределимая система имеет n лиш­ них неизвестных, то система n канонических уравнений для опреде­ ления этих неизвестных в общем виде записывается как система

.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

δn1X1 + δn2X2 + ... + δnnXn + DnF = 0.

Впервом уравнении (9.2) δ11 — перемещение точки приложения первого лишнего неизвестного по собственному направлению выз­

вано действием единичного значения этого неизвестного. Произве­

дение δ11X1 представляет собой перемещение той же точки по тому же направлению, вызванное силой X1.

Второй член δ12X2 есть перемещение той же точки по тому же на­ правлению, вызванное силой X2, и т.д.

Член D1F есть перемещение в том же месте и по тому же направ­ лению, вызванное заданной нагрузкой.

Вцелом вся левая часть первого уравнения представляет собой

суммарное перемещение точки приложения силы X1 по направлению этой силы, вызванное всеми силами (заданными и лишними неиз­ вестными).

Это перемещение приравнивают к нулю, т.к. в заданной системе оно отсутствует.

Второе уравнение выражает то условие, что суммарное переме­

щение точки приложения силы X2 по направлению этой силы от всех воздействий равно нулю.

Смысл остальных уравнений ясен.

Уравнения (9.2) линейные и подчиняются закону Гука. В силу тео­

ремы о взаимности перемещений δ12 + δ21; ... δ1n = δn1; ... δ2n = δn2 и т.д. Коэффициенты δin и DiF определяют либо с помощью интегралов Мора, либо способом Верещагина. Причем коэффициент δin представ­ ляет собой результат перемножения i-х единичных эпюр на n-е единич­

ные эпюры. Величину DiF определяют перемножением эпюры заданных нагрузок (грузовой) на соответствующие i-е единичные эпюры. Следо­

вательно, для нахождения коэффициентов δin и DiF необходимо по­ строить соответствующие эпюры внутренних силовых факторов.

172

Следует отметить, что метод сил можно применять для любой статически неопределимой системы, работающей не только на изгиб, но и на кручение, растяжение или на то, другое и третье совместно.

Трудности расчета статически неопределимых систем состоят не в составлении этих уравнений, а в их решении.

При небольшом числе уравнений они могут быть без затруднений решены способом последовательного исключения неизвестных. При большем числе уравнений применяют специальные приемы, облег­ чающие их решение (способ Гаусса, способ последовательных приб­ лижений, машинный способ).

При решении статически неопределимых рам целесообразно ис­ пользовать их свойства симметрии, как конструктивные, так и на­ грузочные, что позволит значительно упростить решение рам. Рас­ смотрим, например, трижды статически неопределимую раму, кон­ структивно симметричную (рис. 9.6), при постоянной жесткости ее элементов EI = const.

h

Рис. 9.6. Три раза статически неопределимая рама:

а — исходная рама; б — рама, разрезанная сечением; в — эквивалентная система; г — эпюра моментов от Х1 = 1; д — эпюра моментов от Х2 = 1; е — эпюра моментов от Х3 = 1

173

Конструктивно симметричной будет такая рама, у которой правая часть может рассматриваться как зеркальное отображение левой части относительно плоскости симметрии (рис. 9.6, а). Основную систему этой рамы можно изобразить в виде рамы, рассеченной на левую и правую одинаковые части (рис. 9.6, б). Эквивалентная система будет представлять собой рассеченную раму с тремя внутренними силовыми факторами: Х1 — продольная неизвестная сила; Х2 — поперечная сила; Х3 — изгибающий момент.

Из рис. 9.6, видно, что неизвестные Х1 и Х3 являются симметрич­ ными, а неизвестная Х2 — кососимметричной. Построим эпюры мо­ ментов от единичных сил для основной системы (рис. 9.6, г, д, е).

Для рассматриваемой рамы, поскольку она трижды статически неопределима, имеем три канонических уравнения:

Если определять для решения этой системы коэффициенты δ, то можно заметить, что часть из них равна нулю, например

Аналогично получим и для коэффициентов δ21, δ23 = δ32, также равных нулю, т.е. все коэффициенты, содержащие один симметрич­ ный индекс, а второй несимметричный, для такой рамы равны нулю, и система канонических уравнений приобретает вид

Если на раму действует симметричная внешняя нагрузка (рис. 9.7, а), то эпюра грузовых моментов для нее будет также симметрична. Под симметричной нагрузкой понимают такую, при которой все внешние силы, приложенные к одной части рамы, являются зеркальным отоб­ ражением сил, приложенных к левой части (рис. 9.7, а). Под косо­ симметричной нагрузкой понимают такую нагрузку, при которой силы, приложенные к правой половине рамы, также являются зер­ кальным отображением сил, приложенных к левой половине, но противоположны им по знаку (рис. 9.7, б). При определении коэф­ фициента d2F перемножим эпюры моментов (рис. 9.7, а) от внешней

174

F F F F

Рис. 9.7. Примеры нагружения рамы:

а — симметричной нагрузкой; б — кососимметричной нагрузкой

нагрузки на кососимметричную эпюру моментов от единичных сил (рис. 9.6, д). Получаем d2F = 0. При d2F = 0 из второго уравнения си­ стемы (9.4) Х2 также будет равен нулю. Рама может быть нагружена и кососимметричной внешней нагрузкой (рис. 9.7, б). Эпюра момен­ тов при этом также кососимметричная, и перемещения d1F = d3F = 0. В этом случае из (9.4) видно, что симметричные усилия в месте раз­ реза равны нулю: Х1 = Х3 = 0.

Из этого следует:

—для конструктивно симметричной рамы коэффициенты δ, вхо­ дящие в канонические уравнения, содержащие один симметричный индекс, а второй кососимметричный, всегда равны нулю;

—при действии на раму симметричной внешней нагрузки коэф­ фициенты dF, содержащие кососимметричный индекс, равны нулю;

—если на раму действует кососимметричная нагрузка, то коэф­

фициенты dF, содержащие симметричные индексы, равны нулю. Технику расчета простейших статически неопределимых систем

покажем на конкретных примерах.

9.4.ПОРЯДОК РАСЧЕТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ

При решении статически неопределимых балок и рам (систем) целесообразно придерживаться следующей последовательности.

1.Устанавливают степень статической неопределимости системы.

2.Удаляются лишние связи, т.е. исходную систему превращают в статически определимую кинематически неизменяемую, называ­ емую основной системой. Вариантов основных систем может быть несколько. Выбирают наиболее рациональную основную систему с позиций удобства ее решения.

175

3.Основную систему нагружают заданной нагрузкой и неизвест­

ными силовыми факторами X1, X2, …, Xn, заменяющими удаленные связи. Полученную схему нагружения системы называют эквивалентной системой.

4.Для эквивалентной системы составляют канонические уравне­ ния, число которых должно равняться числу лишних неизвестных.

5.Строят грузовую и единичную эпюры лишних неизвестных и соответствующим их перемножением, находят коэффициенты кано­ нических уравнений.

6.После решения канонических уравнений и определения вели­

чины и знака лишних неизвестных X1, X2, …, Xn находят реакции опор и строят эпюры внутренних силовых факторов (N, Q, M).

7.Выполняют статическую и деформационную проверку. Наиболее надежной проверкой правильности определения лиш­

них неизвестных и построения эпюр внутренних силовых факторов для заданной системы является ее повторное решение при другом выборе основной системы. Совпадение окончательных эпюр, по­ лученных в результате двух указанных решений, является гарантией их правильности. Большая трудоемкость такой проверки заставляет в большинстве случаев от нее отказываться, ограничиваясь так на­ зываемыми статической и деформационной проверками. Первая из них заключается в проверке равновесия некоторой отсеченной части рамы под действием приложенных к ней внешних сил и внут­ ренних силовых факторов, заменяющих действие отброшенных частей рамы на оставленную. При деформационной проверке про­ изводится перемножение окончательной эпюры изгибающих мо­ ментов, построенной для заданной системы, на одну из единичных эпюр. Результат указанного перемножения должен быть равен нулю.

Пример 9.1. Построить эпюры поперечных сил Q и изгибающих моментов М для балки, изображенной на рис. 9.8, а. Оценить ее проч­ ность, если поперечное сечение балки выполнено в виде швеллера

№16, материал балки — сталь, [s] = 200 МПа.

Ре ш е н и е. 1. Определяем степень статической неопределимо­ сти балки. В заделке возникают три реакции RAB, RAГ, MA (рис. 9.8, а),

а на шарнирно-подвижной опоре — одна RB. Уравнений равновесия для плоской системы — три. Следовательно, балка один раз статиче­ ски неопределима.

2.Выбираем основную систему, отбрасывая лишние неизвестные. Для данной балки можно предложить только две основные системы (рис. 9.8, б, г). Рациональной будет схема на рис. 9.8, б.

3.Прикладываем к выбранной рациональной основной системе заданную нагрузку M и F и вместо отброшенной опоры В, неизвест­ ную силу Х. Получили эквивалентную систему (рис. 9.8, д).

176

аRAГ

Рис. 9.8. Статически неопределимая балка:

а — заданная схема нагружения балки; б, г — основные системы; в, д — эквивалентные системы; е — схема нагружения балки единичной

силой; ж — единичная эпюра; з — схема нагружения балки моментом M; и — эпюра от нагружения моментом М; к — схема нагружения балки силой F; л — эпюра от нагружения силой F; м — схема нагружения балки заданной нагрузкой и найденной Х; н — эпюра поперечных сил; о — окончательная эпюра моментов

177

10

20 Рис. 9.8. Окончание

4. Далее к основной системе последовательно прикладываем:

—единичную силу 1 (рис. 9.8, е); направление силы выбираем произвольно;

—внешний заданный момент М (рис. 9.8, з);

—внешнюю заданную силу F (рис. 9.8, к).

Заданную нагрузку разделяем, используя принцип «расслоения», рассмотренный в гл. 6, с целью упрощения перемножения эпюр по способу Верещагина.

5.Для этих схем (рис. 9.8, е, з, к) строим эпюры изгибающих мо­ ментов М1 (рис. 9.8, ж) Мм (рис. 9.8, и) и МF (рис. 9.8, л).

6.Записываем каноническое уравнение метода сил. Оно одно, так как балка один раз статически неопределима

δ11X + DF = 0.

7. Определяем коэффициенты канонического уравнения, исполь­ зуя перемножение эпюр по способу Верещагина.

178

Для нахождения коэффициента δ11 умножаем единичную эпюру саму на себя:

Для нахождения коэффициента DF умножаем грузовые эпюры Мм и МF на единичную, результаты суммируем.

Знак «минус» перед вторым слагаемым обусловлен тем, что эпюры М1 и МF расположены по разные стороны от нулевой линии.

8. Подставляя значения δ11 и DF в каноническое уравнение, нахо­ дим

Знак «плюс» перед Х означает, что направление Х выбрано верно. 9. Строим эпюры Q и M . Построение эпюр осуществляем, двига­

ясь от свободного конца балки к заделке.

I участок 0 ≤ z1 ≤ 2 м Q1 = F = 10 кН;

M1 = –F · z1; при z1 = 0 M1 = 0;

при z1 = 2 м M1 = –10 · 2 = –20 кНм. II участок 0 ≤ z2 ≤ 2 м

Q2 = F = 10 кН;

M2 = –F(2 + z2) + M;

при z2 = 0 M2 = –10 · 2 = –20 кНм; при z2 = 2 м M2 = –10 · 4 + 30 = –10 кНм.

III участок 0 ≤ z3 ≤ 2 м

Q3 = F – X = 1 – 17,5 = –7,5 кН; M3 = –F(4 + z3) + M + X · z3;

при z3 = 0 M3 = –10 · 4 + 30 = –10 кНм;

при z3 = 2 м M3 = –10 · 6 + 30 + 17,5 · 2 = 5 кНм. Эпюры Q и M представлены на рис. 9.8, н, о.

179

10. Выполняем деформационную проверку. С этой целью умно­ жаем по способу Верещагина единичную эпюру М1 на эпюру М.

EIxdв = − 12 2 15 132 + 5 2 12 2 = 0.

Полученный результат показал, что балка решена верно, т. к. пе­ ремещение на опоре В отсутствует.

11. Проверяем прочность балки, используя условие прочности

smax = Mmax ≤ [s].

Wmax

Для швеллера № 16 Wx = 93,4 см3, тогда

214 МПа > [σ] = 200 МПа, следовательно, необходимо выбрать поперечное сечение балки с большим номером швеллера, например, № 16 а.

Пример 9.2. Для балки, показанной на рис. 9.9, а, построить эпюры поперечных сил Q и изгибающих моментов M, подобрать из условий прочности поперечное сечение балки в виде двутавра, если [σ] = 160 МПа. Нагрузка и необходимые размеры указаны на схеме балки.

Р е ш е н и е. Раскрываем степень статической неопределимости балки. Балка два раза статически неопределима, т.к. имеет пять не­ известных (три реакции возникают в заделке, а по одной на шарнир­ ных опорах). Для кинематической неизменяемости балки достаточно трех связей.

1.Выбираем основную систему. На рис. 9.9, б, в, г приведены варианты основных систем. Более рациональной для дальнейшего расчета является система на рис. 9.9, г.

2.Создаем эквивалентную систему. Для этого основную систему нагружаем заданной нагрузкой и в местах отброшенных справа шар­

нирных опор прикладываем лишние неизвестные X1 и X2. Направле­ ние их выбираем произвольно. Эквивалентная система представлена на рис. 9.9, д.

3.Составляем канонические уравнения метода сил. Число их равно числу лишних неизвестных.

δ11X1 + δ12X2 + D1F = 0;

δ21X1 + δ22X2 + D2F = 0.

180

29,5 Рис. 9.9. Дважды статически неопределимая балка:

а— заданная схема нагружения балки; б, в, г — варианты основных систем;

д— эквивалентная система; е, ж — единичные эпюры моментов М1 и М2;

з— грузовая эпюра моментов MF; и — эпюра поперечных сил Q; к — эпюра изгибающих моментов после раскрытия статической неопределимости

181

3.Строим эпюры изгибающих моментов от заданной нагрузки F1

иF2 (грузовую) и от единичных сил X1 = 1 и X2 = 1 (единичные). Они изображены на рис. 9.9, е, ж, з.

4.Определяем коэффициенты канонических уравнений δ и ∆, используя способ Верещагина

1. Находим значения X1 и X2. Для этого вводим полученные зна­ чения коэффициентов в канонические уравнения и преобразуем их

Для решения системы уравнений используем матричный способ, т.е. находим определители ∆, ∆1 и ∆2

182

Q2 = –X2 + F = –24,1 + 50 = 25,9 кН;

M2 = X2(2 + z2) – F2z2;

при z2 = 0 M2 = 24,1 · 2 = 48,2 кНм;

при z2 = 3 м M2 = 24,1 · 5 – 50 · 3 = 29,5 кНм. III участок 0 ≤ z3 ≤ 3 м

Q3 = –X2 + F2 – X1 = –24,1 + 50 – 40,3 = 14,4 кН; M3 = X2(5 + z3) – F2(3 + z3) + X1 · z3;

при z3 = 0 M3 = 24,1 · 5 – 50 · 3 = 29,5 кНм;

при z3 = 3 м M3 = 24,1 · 8 – 50 · 6 + 40,3 · 3 = 5 кНм. IV участок 0 ≤ z4 ≤ 2 м

Q4 = –X2 + F2 – X1 + F1 = –24,1 + 50 – 40,3 + 30= 15,6 кН; M4 = X2(8 + z4) –F2(6 + z4) + X1(3 + z4) – F1 · z4;

при z4 = 0 M4 = 24,1 · 8 – 50 · 6 + 40,3 · 3 = 13,5 кНм; при z4 = 2 м M4 = 24,1 · 10 – 50 · 8 + 40,3 · 5 – 30 · 2 = 17,5 кНм.

Эпюры поперечных сил Q и изгибающих моментов М статически неопределимой балки представлены на рис. 9.7, и, к.

183

2. Используя условие прочности, подбираем двутавровую балку

По ГОСТ 8239-72 этому моменту сопротивления соответствует двутавровая балка № 24 а (прил. 2).

Пример 9.3. Построить эпюры продольных сил N, поперечных Q

иизгибающих моментов М для рамы, изображенной на рис. 9.10, а. Жесткость всех участков рамы одинаковая EI = const, l = 1 м; F = 25 кН.

Ре ш е н и е. 1. Определяем степень статической неопредели­ мости рамы. Ее неподвижность обеспечивают четыре реакции опор

(RAB, RAГ, MA, RB, рис. 9.10, а), а достаточно трех. Следовательно, рама один раз статически неопределима.

2. Выполняем основную систему, отбрасывая лишнюю связь (рис. 9.10, б, в).

3. Прикладываем к основной системе заданную нагрузку (силу F)

ивместо отброшенной лишней связи неизвестную Х, получаем эк­ вивалентные системы (рис. 9.10, г, д).

4. Далее к выбранной рациональной основной системе (рис. 9.10, б) последовательно прикладываем:

— внешнюю нагрузку (рис. 9.10, е);

— единичную силу (рис. 9.10, з).

5. Для этих схем строим единичную М1 и грузовую MF эпюры (рис. 9.10, ж, и).

6. Составляем каноническое уравнение

δ11X + D1F = 0.

7. Находим коэффициенты этого уравнения соответствующим перемножением эпюр по способу Верещагина.

Для нахождения коэффициента δ11 умножаем эпюру М1 саму на себя, а D1F — эпюру М1 на МF.

184

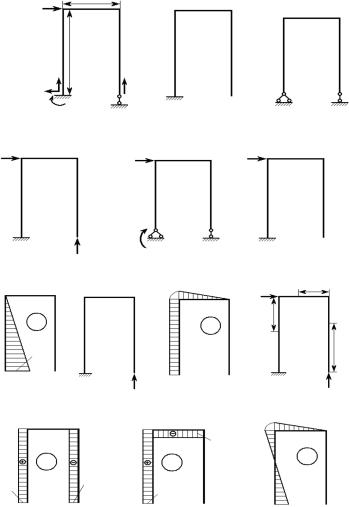
Рис. 9.10. Статически неопределимая рама один раз:

а — заданная схема нагружения рамы; б, в — основные системы; г, д — эквивалентные системы; е — схема нагружения рамы заданной

нагрузкой; ж — грузовая эпюра; з — схема нагружения рамы силой, равной единице; и — единичная эпюра; к — схема нагружения рамы заданной

нагрузкой и найденной реакцией RB = 67 F; л — эпюра продольных сил N;

м — эпюра поперечных сил Q; н — эпюра изгибающих моментов М

185

Подставляя коэффициенты в уравнение, получаем

8. Строим эпюры N, Q и М, учитывая найденное выше значение X (рис. 9.10, к)

I участок 0 ≤ z1 ≤ 2 м N1 = –X = –21,43 кН

Q1 = 0;

M1 = 0.

II участок 0 ≤ z2 ≤ 1 м

N2 = 0;

Q2 = –X = –21,43 кН;

Эпюры N, Q и М показаны на рис. 9.10, л, м, н.

9. Выполняем деформационную проверку, перемножая эпюру М1 на эпюру М.

Перемещение опоры В в направлении X равно

EIxdв = 12 21,43 1 321 + 2 21,43 1 − 1250 2 1 = 0,

что соответствует условиям закрепления рамы (вертикальное пере­ мещение опоры В невозможно).

Пример 9.4. Построить эпюры внутренних силовых факторов N, Q, М для статически неопределимой рамы, представленной на рис. 9.11, а, если жесткость сечений элементов рамы EI = const. На­ грузка и необходимые размеры указаны на схеме рамы.

Р е ш е н и е. 1. Устанавливаем степень статической неопредели­ мости рамы. Рама имеет пять неизвестных (три в заделке и две на опоре), значит, она дважды статически неопределима внешним об­ разом.

2. Удаляем левую опору и получаем основную систему рамы (рис. 9.11, б).

186

Рис. 9.11. Дважды статически неопределимая рама:

а— заданная схема нагружения рамы; б — основная система;

в— эквивалентная система; г — грузовая эпюра; д, е — единичные эпюры

3.Создаем эквивалентную систему, для чего заменяем левую

опору лишними неизвестными Х1 и Х2, и прикладываем их и задан­ ную нагрузку F (рис. 9.11, в) к основной системе.

4.Составляем канонические уравнения

δ11X1 + δ12X2 + D1F = 0;

δ21X1 + δ22X2 + D2F = 0.

5. Для решения этой системы уравнений строим эпюру моментов для основной системы рамы только от внешней нагрузки на сжатых волокнах (рис. 9.11, г). Кроме этого, строим эпюры моментов от еди­ ничных нагрузок Х1 = 1; Х2 = 1 (рис. 9.11, д, е) также на сжатых волокнах.

6. Находим коэффициенты канонических уравнений δ и , ис­ пользуя метод Верещагина.

При определении коэффициента δ11 производим перемножение площади единичной эпюры моментов Ω = 6 · 6 / 2 на ординату под

центром тяжести площади этой эпюры yc = 326.

187

Коэффициент d12 определяется как произведение площади эпюры моментов от первой единичной силы на ординату второй эпюры, взятую под центром тяжести первой, отнесенное к жесткости сече­ ния рамы

Согласно теореме взаимности работ и перемещений

δ12 = δ21.

Коэффициент d22 найдется от перемножения второй единичной эпюры на саму себя

Коэффициенты 1F и 2F найдем, перемножая площади эпюры моментов от внешней нагрузки (рис. 9.11, г) на соответствующие ординаты под центром тяжести грузовой эпюры, взятые на эпюре моментов от единичных сил. Перемножение производим по участкам нагружения, суммируя произведения

Ординаты под центром тяжести второй площади (площадь треу­ гольника) на эпюрах единичных сил равны нулю.

7.После преобразования канонические уравнения приведем

квиду

72X1 + 36X2 + 720 = 0;

36X1 + 26,66X2 + 480 = 0.

188

Решая эту систему уравнений, имеем X1 = –3 кН; X2 = –14 кН. Таким образом, освобождаются от статической неопределимости

рамы.

Зная X1 и X2 и используя обычные приемы построения эпюр, вы­ полняем построение эпюр N, Q, и M.

7. На рис. 9.12, а показана схема нагружения рамы после раскры­ тия статической неопределимости.

Для построения эпюр N, Q, и M разобьем раму на три участка и найдем силовые факторы, действующие по их длине.

I участок 0 ≤ z1 ≤ 2 м N1 = Х1 = 3 кН;

Q1 = –X2 = –14 кН;

в г

Рис. 9.12. Рама после раскрытия статической неопределимости:

а— схема нагружения; б — эпюра продольных сил N;

в— эпюра поперечных сил Q; г — эпюра изгибающих моментов М

189

при z2 = 6 м M3 = 14 · 2 + 3 · 6 – 20 · 2 = 6 кНм.

Эпюры N, Q, и M представлены на рис. 9.12, б, в, г. Окончательную эпюру моментов можно также получить путем алгебраического сло­ жения эпюры моментов только от внешней нагрузки и эпюр от еди­ ничных нагрузок, умноженных соответственно на величину Х1 и Х2.

8. Выполняем деформационную проверку. С этой целью перемно­ жаем по способу Верещагина эпюру М (рис. 9.12, г) на единичную эпюру М1 (рис. 9.11, д)

Полученный результат перемножения эпюр показал, что действи­ тельно перемещение на левой опоре в направлении Х1 отсутствует (равно нулю). Задача решена верно.

Пример 9.5. Построить эпюры внутренних силовых факторов для рамы, изображенной на рис. 9.13, а, если q = 10 кН/м; h = 5 м; l = 2 м; EI = const.

Решение. 1. Определяем степень статической неопределимости рамы. Условия закрепления дают пять реакций связей (RAB, RAГ, MA, RB и RC, рис. 9.13, а). Необходимы — три. Следовательно, рама два раза статически неопределима.

2.Выбираем основные системы (рис. 9.13, б, в).

3.Нагружаем основные системы заданной нагрузкой q и лиш­

ними неизвестными Х1 и Х2, получаем эквивалентные системы (рис. 9.13, г).

4.Записываем канонические уравнения

δ11X1 + δ12X2 + D1F = 0; δ21X1 + δ22X2 + D2F = 0.

190

A RAГ

MA

ll

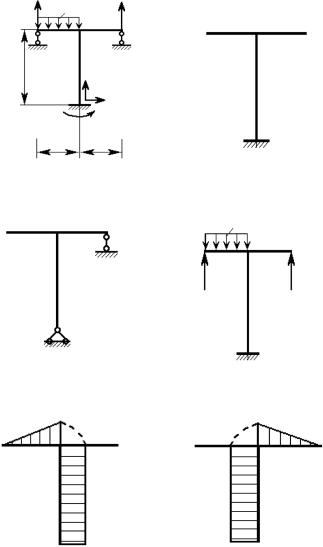
Рис. 9.13. Статически неопределимая рама:

а — заданная схема нагружения; б, в — основные системы;

г— эквивалентная система; д — единичная эпюра при Х1 = 1;

е— единичная эпюра при Х2 = 1; ж — грузовая эпюра; з — схема нагружения рамы заданной нагрузкой и найденными реакциями; и — эпюра продольных сил N; к — эпюра поперечных сил Q; л — эпюра изгибающих моментов M

191

192

5.Строим эпюры изгибающих моментов от единичных сил X1 = 1

иХ2 = 1 и от распределенной нагрузки q (рис. 9.13, д, е, ж).

6.Находим коэффициенты канонических уравнений перемноже­ нием соответствующих эпюр по способу Верещагина

Подставляя значения коэффициентов в канонические уравнения метода сил, имеем

Тогда

X2 = Rc = 2,35 кН; X1 = RВ = 12,66 кН.

Рама с заданной нагрузкой q и найденными лишними реакциями RВ и Rc изображена на рис. 9.13, з.

7. Строим эпюры N, Q, и M.

I участок 0 ≤ z1 ≤ l м N1 = 0;

Q1 = RB – qz1; при z1 = 0 Q1 = 12,66 кНм;

при z1 = 2 м Q1 = 12,66 – 10 · 2 = –7,34 кНм.

z2

M1 = RB z1 − q 21 ; при z1 = 0 M1 = 0;

193