6.2.СПОСОБ ВЕРЕЩАГИНА

Недостатком метода вычисления перемещений с использованием интегралов Мора является необходимость составления аналитического выражения подинтегральных функций и сам процесс интегрирования. Это особенно неудобно при определении перемещений для бруса с большим числом участков нагружения.

Если же брус состоит из прямых участков с постоянной в пределах участка жесткостью, операцию интегрирования можно упростить. По способу Верещагина операция интегрирования заменяется перемножением площади Ω эпюры М(z) от заданной нагрузки на ор­ динату yc эпюры М1(z) от единичной нагрузки, взятой под центром тяжести площади Ω эпюры М(z).

Способ перемножения эпюр предложен в 1925 г. студентом Московского института инженеров железнодорожного транспорта А.Н. Верещагиным.

Для отдельного участка балки это правило формулируется следующим образом: каждое из слагаемых, входящих в интеграл Мора, равно произведению площади Ω нелинейной эпюры изгибающих моментов на

ординату yc линейной эпюры, взятую под центром тяжести нелинейной, деленному на жесткость сечения (EIx) данного участка балки.

Для определения линейного или углового перемещения, т. е. вычисления интеграла Мора в целом, следует просуммировать указанные слагаемые для всех участков балки.

Вычисление интеграла Мора по правилу Верещагина часто называют способом перемножения эпюр. При этом эпюру МF по-прежнему называют грузовой, а эпюру М1 — единичной.

Есть случаи, когда вычисление интеграла Мора не может быть выполнено по правилу Верещагина. Это относится, во-первых, к брусьям с криволинейной осью — для них обе эпюры изгибающих моментов МF и М1 нелинейны; во-вторых, к балкам с непрерывным переменным сечением, для которых величина EIx не может быть вынесена за знак интеграла, следовательно, не применимы преобразования, выполнявшиеся при выводе правила Верещагина.

Приведем некоторые практические указания по применению правила Верещагина.

1. Произведение площади нелинейной эпюры на ординату линейной считается положительным, если площадь и ордината расположены по одну сторону от нулевой линии (обе положительны или обе отрицательны). В противном случае произведение площади на ординату — величина отрицательная.

109

2.Если в пределах данного участка обе эпюры линейны, то принципиально безразлично, площадь какой эпюры брать и на какой эпюре — ординату.

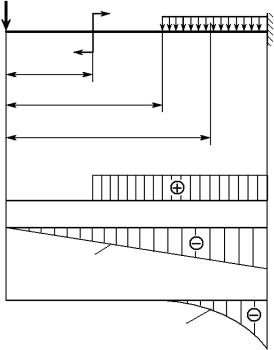
3.Во многих случаях оказывается удобным строить грузовую эпюру в так называемом «расслоенном» виде. Сущность этого расслоения состоит в использовании принципа суперпозиции: строят эпюры изгибающих моментов отдельно от каждой из заданных нагрузок (рис. 6.3).

4.При сложном очертании эпюры МF или М1 их делят на простые эпюры, площади и положение центра тяжести которых известны.

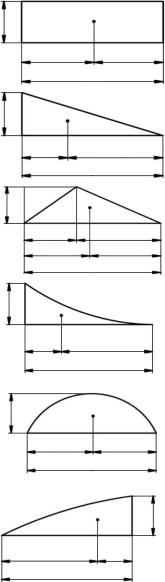
В табл. 6.1 приведены величины площадей и координаты центров тяжести отдельных геометрических фигур, а в прил. 5 — произведения площадей и ординат подобных фигур.

III

a

b

z

M

а

б

Fz

в

q(z – b)2 / 2

Рис. 6.3. Грузовая эпюра в «расслоенном» виде:

а— от момента М; б — от сосредоточенной силы F;

в— от распределенной нагрузки q

110

111

Таким образом, при определении перемещений с использованием правила Верещагина соблюдают следующую последовательность:

—строят эпюры внутренних силовых факторов от заданной нагрузки (грузовую эпюру);

—сняв заданную нагрузку, прикладывают единичную силу (или единичный момент) в сечении, перемещение которого определяют, и строят от нее эпюры внутренних силовых факторов (единичные эпюры);

—перемножают эпюры по способу Верещагина, тем самым вычисляют интеграл Мора.

Пример 6.3. Для балки (рис. 6.1, а), рассмотренной в примере 6.1, выполнить определение прогиба в т. А и угла поворота в т. В с использованием способа Верещагина. Сравнить полученные результаты

срешением примера 6.1.

Р е ш е н и е. 1. Строим эпюру изгибающих моментов от заданной нагрузки (рис. 6.1, б).

2. Строим эпюру от единичной силы (рис. 6.1, г).

3. Перемножаем эти эпюры по способу Верещагина, Так как обе эпюры линейные, не имеет значения, где брать площадь, а где ординату.

δ A = Σ Ω yc .

EIx

Участок I. Умножаем площадь треугольника единичной эпюры М1 на ординату грузовой эпюры МF. Так как обе эпюры имеют разные знаки, перед их произведением ставим знак «минус».

Участок II. Эпюры МF и М1 (имеют вид трапеции) на этом участке разбиваем на более простые фигуры — прямоугольник и треугольник, для которых известны положения центров тяжести. Обе эпюры имеют разные знаки, перед их произведением ставим знак «минус».

Складывая прогибы участков, имеем

δA = −14 мм.

112

4.Строим эпюру от единичного момента (рис. 6.1, е).

5.Перемножаем эпюры МF (рис. 6.1, б) и М2 (рис. 6.1, е) по способу Верещагина. Тогда угол поворота сечения в т. В будет равен:

Участок I

θBI = 0, т.к. на I участке эпюра М2 = 0.

Участок II: умножаем площадь прямоугольника эпюры М2 на ординату эпюры МF — среднюю линию трапеции.

Полученные результаты вычислений по методу интегралов Мора и способу Верещагина абсолютно идентичны. Знаки результатов вычислений пояснены в примере 6.1.

Пример 6.4. Определить прогиб в т. В и угол поворота сечения в т. А консольной балки (рис. 6.4, а), нагруженной сосредоточенной силой F =50 кН и распределенной нагрузкой q = 10 кН/м, используя способ Верещагина. Жесткость балки постоянна и равна EIx = 1· 104 кНм2.

Р е ш е н и е. 1. Строим эпюру изгибающих моментов от заданной нагрузки:

I участок 0 ≤ z ≤ 2 м

II участок 0 ≤ z ≤ 1 м M = –q · 2(1 + z);

при z = 0 М = –q · 2(1 + 0) = –10 · 2 · 1 = –20 кНм; при z = 1 м M = –q · 2(1 + 1) = –10 · 2 · 2 = –40 кНм.

III участок 0 ≤ z ≤ 2 м

M = –q · 2(1 + 1 + z) + F · z;

при z = 0 М = –q · 2(2 + 0) = –10 · 2 · 2 = –40 кНм; при z = 2 м M = –q · 2(2 + 2) = –10 · 2 · 4 = –80 кНм;

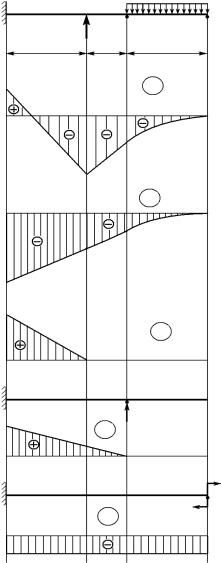
Эпюра изгибающих моментов от заданной нагрузки представлена на рис. 6.4, б.

2. Для перемножения эпюр по способу Верещагина выше построенная эпюра представляет некоторую сложность, так как пересекает нулевую линию (меняет знак), поэтому необходимо найти коорди-

113

Рис. 6.4. Эпюры изгибающих моментов консольной балки с эффектом «расслоения»:

a — схема нагружения; б — эпюра от заданной нагрузки; в — эпюра только от распределенной нагрузки q; г — эпюра только от силы F; д — нагружение балки единичной силой; е — эпюра от единичной силы; ж — нагружение балки единичным моментом; з — эпюра от единичного момента

114

нату z точки пересечения. Будем решать задачу, используя эффект «расслоения» эпюр, т. е. построим грузовую эпюру, как сумму двух составляющих:

—отдельно от распределенной нагрузки q;

—отдельно от сосредоточенной силы F.

3. Строим грузовую эпюру Mq от распределенной нагрузки q: I участок 0 ≤ z ≤ 2 м

II участок 0 ≤ z ≤ 1 м

Mq = –q · 2(1 + z);

при z = 0 Мq = –q · 2(1 + 0) = –10 · 2 · 1 = –20 кНм; при z = 1 м Mq = –q · 2(1 + 1) = –10 · 2 · 2 = –40 кНм.

III участок 0 ≤ z ≤ 2 м

Mq = –q · 2(1 + 1 + z);

при z = 0 Мq = –q · 2(2 + 0) = –10 · 2 · 2 = –40 кНм; при z = 2 м Mq = –q · 2(2 + 2) = –10 · 2 · 4 = –80 кНм;

при z = 2 м MF = F · 2 = 50 · 2 = 100 кНм. Эпюра MF приведена на рис. 6.4, г.

5. Строим эпюру изгибающих моментов от единичной силы, приложенной в т. В, т.к. именно в этой точке необходимо определить прогиб. Направление силы выбираем произвольно:

6. Строим эпюру изгибающих моментов от единичного момента, приложенного в т. А, т.к. именно в этой точке необходимо определить

115

угол поворота сечения балки. Направление момента выбираем произвольно:

I; II и III участки 0 ≤ z ≤ 5 м

М2 = −1.

7. Определяем угол поворота сечения в т. А по правилу Верещагина, перемножая эпюры Mq; MF и M2

Полученный в результате расчета знак при θА указывает, что направление угла поворота задано верно выбранным направлением единичного момента (рис. 6.4, ж).

8. Определяем прогиб в т. В, используя способ Верещагина и перемножая эпюры Mq; MF и M1 :

и M1 расположены по одну сторону от нулевой линии, их произведение положительно.

Знак δB указывает, что балка прогнется вниз, а не вверх, как предполагалось при выборе направления единичной силы вверх.

Пример 6.5. Определить прогиб в т. В и угол поворота сечения в т. А консольной балки (рис. 6.5, а), нагруженной сосредоточенной силой F = 20 кН, моментом М = 10 кНм и распределенной нагрузкой q = 40 кН/м, используя способ Верещагина. Жесткость балки постоянна и равна EIx = 1·104 кНм2.

116

Рис. 6.5. Эпюры изгибающих моментов консольной балки с эффектом «расслоения»:

а— схема нагружения; б — эпюра от момента М и сосредоточенной силы F;

в— эпюра от распределенной нагрузки q; г — эпюра от М = 1;

д— эпюра от F = 1

Ре ш е н и е. 1. Решаем задачу, используя эффект «расслоения» эпюр, т.е. построим грузовую эпюру как сумму двух составляющих:

— отдельно от распределенной нагрузки q;

— отдельно от сосредоточенной силы F и момента М.

2. Строим грузовую эпюру MF от сосредоточенной силы F и момента М

117

III участок 0 ≤ z ≤ 1 м MF = M + F(1 + 1 + z);

при z = 0 MF = M + F(1 + 1 + 0) = 10 + 20 · 2 = 50 кНм; при z = 1 м MF = M + F(1 + 1 + 1) = 10 + 20 · 3 = 70 кНм.

Эпюра MF приведена на рис. 6.5, б.

3. Строим грузовую эпюру Mq от распределенной нагрузки q: I участок 0 ≤ z ≤ 1 м

Mq = 0;

II участок 0 ≤ z ≤ 1 м

Mq = 0;

III участок 0 ≤ z ≤ 1 м

Эпюра Mq приведена на рис. 6.5, в.

4.Строим эпюру изгибающих моментов от единичного момента, приложенного в т. А, т.к. именно в этой точке необходимо определить угол поворота сечения балки. Направление момента выбираем произвольно:

I участок М1 = 0;

II и III участки М1 = 1.

5.Строим эпюру изгибающих моментов от единичной силы, приложенной в т. В, т.к. именно в этой точке необходимо определить прогиб. Направление силы выбираем произвольно

I участок 0 ≤ z ≤ 1 м M1 = 0. II участок 0 ≤ z ≤ 1 м M1 = 0.

III участок 0 ≤ z ≤ 1 м M1 = 1 · z; при z = 0 M1 = 0;

при z = 1 м M1 = 1 · 1 = 1.

Эпюра M1 приведена на рис. 6.5, д.

6. Определяем угол поворота сечения в т. А по правилу Верещагина, перемножая эпюры Mq; MF и M1:

При EIx = 1·104 кНм2 qА = 0,0093 рад.

118