Добавил:

Mehanik Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Технология машиностроения

Файл:

Radzevich, S.P. Monograph - 2001

.pdf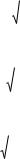

Скачиваний:

Добавлен:

23.02.2023

Размер:

24.47 Mб

Скачать

☆

<<< < Предыдущая 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 5556 / 6056 57 58 59 60 > Следующая >>>

550 9. Топология формообразованных поверхностей деталей

cos ( X

(K) , Z

) cosU

T.д(и)

д(и)

T.д(и)

Аналогично направление касательной к VT.д(и)

линии

учетом

выбранного

направления отсчета

VT.д(и) параметра определим столбцовой матрицей

cosU

]sin V

1.д(и)

2.д(и)

T.д(и)

(V)

T.д(и)

cosU

T.д(и)

]cosV

1.д(и)

2.д(и)

T.д(и)

д(и)

T.д(и)

Косинусы углов, которые направление T (V)

составляет с осями системы координат X

T.д(и)

д(и)

T.д(и) T.д(и)

поверхности заменяющего тора Tд(и) , соответственно равны:

cos ( y(K) , X

T.д(и)

) sinV

;

cos ( y(K)

) cosV

;

cos ( y(K)

, Z

T.д(и)

) 0 .

д(и)

T.д(и)

д(и)

T.д(и)

д(и)

Третья ось zд( K(и))

локальной системы координат xд(K(и)) yд(K(и)) zд(K(и))

направлена вдоль нормали NT.д(и)

к по-

верхности заменяющего тора Tд(и) . Направление нормали

NT.д(и)

к поверхности тора Tд(и) определяется

вектором:

rT.д(и)

iT.д(и)

T.д(и)

sin U

T.д(и)

cosV

T.д(и)

2.д(и)

T.д(и)

[R1.д(и)

R2.д(и)

R2.д(и) cosUT.д(и) ]sin VT.д(и)

jT.д(и)

k T.д(и)

R2.д(и) sin UT.д(и) sin VT.д(и)

R2.д(и) cosUT.д(и)

[R1.д(и) R2.д(и)

R2.д(и) cosUT.д(и) ]cosVT.д(и)

Нормаль NT.д(и)

направлена от тела материального носителя формы поверхности Tд(и) тора.

Косинусы углов,

которые

направление нормали

NT.д(и)

составляет

с осями

системы

координат

XT.д(и)YT.д(и) ZT.д(и) , соответственно равны:

cos (zд(K(и)) , XT.д(и) )

cosUT.д(и) cosVT.д(и)

;

cos2 U

sin 2 U

cos2

T.д(и)

cos (z(K)

)

cosUT.д(и) sinVT.д(и)

;

д(и)

T.д(и)

cos2 U

sin 2 U

cos2 2V

T.д(и)

cos (zд(K(и)) , ZT.д(и) )

sin UT.д(и)

cos 2VT.д(и)

cos

2 U

sin 2 U

T.д(и)

cos 2 2V

T.д(и)

9.7. О допустимости применения принципа суперпозиции при расчете результирующей погрешности формообразования

551

Приведенные результаты позволяют составить оператор Rs (Tд(и) K)

результирующего прямого

sin UT.д(и)

cosVT.д(и)

sin UT.д(и) sin VT.д(и)

cosUT.д(и)

sin VT.д(и)

cosVT.д(и)

cosU

T.д(и)

cosV

sin V

sin U

T.д(и)

cos2 2V

T.д(и)

Rs (T

д(и)

cos2 U

sin 2 U

cos2 V

T.д(и)

Rs (K T

) Rs 1 (T

K) обратного

д(и)

sin UT.д(и)cosVT.д(и)

sin VT.д(и)

cosUT.д(и) cosVT.д(и)

sin U

T.д(и)

sinV

cosV

sin V

T.д(и)

cosUT.д(и)

sin UT.д(и) cos

2VT.д(и)

RT.д(и) rT.д(и)

Rs (K T

)

д(и)

cos2 U

sin 2 U

cos2 V

T.д(и)

преобразования координат.

Локальные системы координат x( K) y

( K) z

(K) и

x(K) y(K) z(K) имеют противоположно направленные оси

и и

аппликат, вокруг которых они развернуты на угол относительной локальной ориентации.

Вектор скорости движения формообразования расположен в общей касательной плоскости и направлен под некоторым углом к первому главному направлению поверхности тора Tд . В сечениях для расчета высоты

и других параметров остаточного детерминированного регулярного микрорельефа нормальные кривизны Rд(и) поверхностей торов Tд(и) не равны главным их кривизнам и могут быть найдены по формуле Эйлера

исходя из значений R1.д(и) и R2.д(и) .

На многокоординатных станках с ЧПУ применяют относительно простой режущий инструмент, которому придают сложное многопараметрическое движение относительно детали. В процессе обработки в результате точечного касания сложной поверхности детали и исходной инструментальной поверхности имеет место дискретное формообразование поверхности Д (см. выше, раздел 9.1).

Расчет величин элементарных составляющих hВ и hП результирующей погрешности формообразования h производится по зависимостям (10) и (13) (см. выше, раздел 9.1). Обычно полагают, что результирующая погрешность формообразования h равна сумме ее элементарных составляющих, т.е. допускают справедливость соотношения1:

h hВ hП ,

(9.64)

а при грубых расчетах, более того, пренебрегают и величиной составляющей hВ , образованной вдоль строки формообразования.

1Помним, что в общем случае справедливо соотношение h ahВ bhП (см. с. 518).

552	9. Топология формообразованных поверхностей деталей

Формула (64) позволяет расчитать величину результирующей погрешности формообразования в текущей точке на поверхности Д детали1, в том числе и в вершинах элементарной формообразованной ячейки на Д ,

когда справедливы соотношения hВ hВ(max) , hП hП(max) и h h(max) и, следовательно, уместна формула

h(max) hВ(max) hП(max) .

Зависимость (64) является приближенной, поскольку основана на предположении о допустимости применения принципа суперпозиции существенно нелинейно коррелируемых между собой элементарных составляющих результирующей погрешности формообразования.

Использование принципа суперпозиции (принципа наложения) предполагает, что результатом сложного эффекта является сумма результатов от всех составляющих его элементарных эффектов при условии, что последние взаимно не влияют один на другой. Поэтому принцип алгебраической суперпозиции строго справедлив лишь к эффектам, описываемым линейными соотношениями. Из формул (10) и (13) очевидно следует, что

составляющие hВ и hП в пределах элементарной ячейки на Д изменяются существенно нелинейно. В этой

связи правомерна постановка вопроса об определении области допустимого применения принципа суперпози-
ции при расчете результирующе погрешности формообразования поверхностей деталей. Допустимость или
			недопустимость применения принципа суперпозиции суще-
	Tи		ственно изменяет подходы к расчету точности и определе-
YT.и	Tи		нию эффективности формообразования.
			Чтобы воспользоваться зависимостью (64), необходи-
			мо определить условия, при которых результирующая по-
			грешность формообразования h с приемлемой точностью
		ZT.и	подчиняется принципу суперпозиции элементарных со-
	X	ZT.и	ставляющих	hВ и hП . Для этого достаточно сопоставить
	T.и		значения результирующей погрешности формообразования
			значения результирующей погрешности формообразования
	(K)		h , определенной по формуле (64) с учетом (10) и (13), с
	(K)		ее значением	~
	xд		ее значением	h , полученным более точным методом, не
rд	Nд	И	требующим использования принципа суперпозиции эле-
rд	Д	И	требующим использования принципа суперпозиции эле-
д	Д	rд	ментарных составляющих результирующей погрешности
	K	д	формообразования.
(K)		д	Точное значение результирующей погрешности фор-
(K)				~
zд	XT.д		мообразования h может быть расчитано исходя из ло-
		yд(K)	кальной аппроксимации поверхностей Д(И) поверхностя-
			ми заменяющих торов Tд(и) .
ZT.д			Процесс формообразования поверхности детали рас-
ZT.д			смотрим в течение промежутка времени, когда формирует-
		YT.д	ся одна элементарная ячейка на Д . В точке K касания обе
			поверхности	Д(И) локально аппроксимируются поверх-

Tд

Рис. 9.12. Относительное положение поверхно-

стей заменяющих торов Tд и Ти .

ностями торов Tд(и) . Поэтому образование результирую-

щей погрешности формообразования h можно проанали-

зировать по схеме (рис.9.12).

С локальным участком поверхности заменяющего тора удобно связать поверхность T[h] , отстоящую от поверх-

ности Tд на расстояние [h] h , равное допуску на точность формообразования поверхности Д (рис. 9.13). Тогда

“погружая” поверхность Tи в пространство между поверхностями Tд и T[h] (в пространство допуска) и вводя

1Если элементарные ячейки на обработанной поверхности детали имеют форму шестиугольников (см. выше. рис. 8.30 на с. 498), используются другие зависимости для расчета величины результирующей погрешности формообразования h

9.7. О допустимости применения принципа суперпозиции при расчете результирующей погрешности формообразования		553
ее в касание	в точке К с поверхностью Tд , полу-чим формообразованную элементарную ячейку	на
поверхности	Д детали. Проекция границ элементарной ячейки на общую к поверхностям заменяющих торов

касательную плоскость является вписанной в замкнутую линию пересечения поверхностей T[h]		и Tи .
Ти	R1.и	Тд
	Nд
T[h]	R2.и
T[h]

Xи

	XT.и
	Yи
	rT.и
Zи	Res (И Ти )
	ZT.и YT.и	Д р	R1.д	R2.д
	Nд	n 2.д	n1.д
	Дн		n1.д

n3.д	n 4.д	2д
	n 4.д	K
		K

		3д	P			1д
			P			hП

		hВ
		hВ
XT.д		Q 4д			h	SВ
XT.д	SП
		rT.д
ZT.д		Xд
YT.д
	Res ( Д Тд)			Yд
				Yд
		Zд
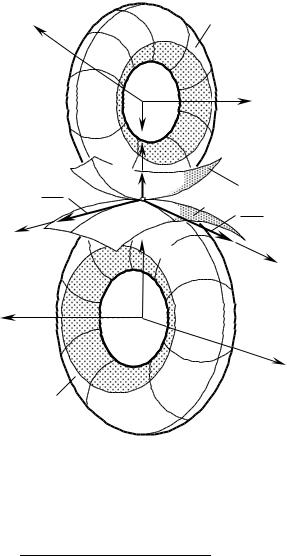
Рис. 9.13. Элементарная ячейка на формообразованной поверхности Д детали.
Погрешность	~	измеряется вдоль нормали к тору Tд				, проходящей через вершину P	элементарной
Погрешность	h	измеряется вдоль нормали к тору Tд				, проходящей через вершину P	элементарной
ячейки и пересекающей поверхность Tд			в точке Q : PQ h . Очевидно, что точка P лежит на поверхности
заменяющего тора Tи ,		а в пределах дуг	SВ	и SП	соответствующие радиусы кривизны поверхностей Tд(и)
постоянны. С учетом принятых допущений (см. выше), проведенные через основания 1д ,							2д , 3д	и 4д
вершин элементарной ячейки нормали n1.д ,				n 2.д , n 3.д и n 4.д		будут попарно: n1.д и n 2.д ; n1.д	и n 3.д ;	n1.д и
n 4.д ; n 2.д и n 3.д ;	n 2.д	и n 4.д ; n 3.д и n 4.д		компланарны.

554	9. Топология формообразованных поверхностей деталей

Если вести речь о наивыгоднейшем формообразовании поверхности детали, величина погрешности h

во всех вершинах элементарной ячейки одинакова, а точка К отстоит от границ элементарной ячейки на расстояния 0,5 SВ и 0,5 SП . Это следствие того, что при наивыгоднейшем формообразовании используются все

резервы и потенциальные возможности процесса фор-

90 ( )

мообразования заданной поверхности детали.

Чтобы получить

точное значение

погрешности

необходимо определить коорди-

C1.и

формообразования h ,

наты точки Q , провести через нее нормаль к тору Tд ,

1.д

рассчитать координаты точки P как точки пересечения

C2.и

проведенной нормали с тором Tи . После этого можно

(K)

zд

S Bz

S Пz

0,5SП

определить погрешность h как расстояние между точ-

C2.

SBy

rQ*z

ками P и Q .

С общей для поверхностей Д и И точкой К (см.

рис. 9.12) свяжем начало локальной системы координат

x(K) y(K) z(K) , оси которой направим параллельно соот-

S П

S Пy

ветствующим

осям системы координат

XT.дYT.дZT.д

rQ*

поверхности заменяющего тора Tд . Тогда в координат-

ной плоскости

y(K) z(K) следы главных секущих плос-

костей

C1.д и

C2.д поверхности Д детали совпадут с

y(K)

осями координат yд(K)

и zд( K) , а следы главных секу-

щих плоскостей C1.и и C2.и поверхности И будут раз-

Рис. 9.14. Локальная

подвижная

система коор-

вернуты относительно этих же координатных осей на

угол

относительной локальной ориентации поверх-

динат.

ностей

Д и И (рис. 9.14). Направление подачи S В

со-

ставляет угол с первым главным сечением C1.и

по-

верхности

И ,

а направление подачи S П

ортогонально направлению подачи S В . Точка Q* лежит в общей

касательной плоскости (см. рис. 9.14), где ее положение определяется радиус-вектором rQ* S В S П .

В проекциях на координатные оси направления подач S В и S П

можно представить так:

(9.65)

SВ

cos( ) k

SВ

sin( ) ;

(9.66)

SП

sin( ) k

SП

cos( ) .

С учетом (65) и (66) справедливо равенство

SВ cos( ) SП sin( )

SВ sin( ) SП cos( )

k K .

Считаем, что “в малом” поверхность тора Tд допускает разворачиваемость на плоскость. Для этого достаточно, чтобы локально выполнялось условие Φ1.д 0 . Такое допущение правомерно, поскольку локально любая поверхность может рассматриваться как разворачивающаяся на плоскость. Тогда положение точки Q

на поверхности тора Tд определится положением точки Q* в общей касательной плоскости.

9.7. О допустимости применения принципа суперпозиции при расчете результирующей погрешности формообразования 555

Найдем проекции r *

и r *

радиус-вектора

r *

на оси координат

y(K)

z( K)

Q Y

Q Z

rQ*Y rQ* cos ;

rQ*Z rQ* sin ,

где – угол между радиус-вектором r * и осью y

(K)

(см. рис. 9.14).

Из рис. 9.14 следует, что

[90 ( )] arctan

SВ

SП

Считаем, что при локальном наложении общей касательной плоскости на поверхность заменяющего тора

r *

точка Q* наложится на точку Q . Тогда в системе координат

T.д

для точки Q имеем следую-

T.д

щие параметры:

rQ*Z

rQ* sin

;

rQ*Y

rQ* cos

(9.67)

rT.д

где rT.д – радиус образующей окружности тора Tд .

Подставив расчитанные по (67) параметры Q и Q точки Q в уравнение поверхности заменяющего

тора

Tд , получим значения декартовых

координат

XQ ,

точки

в системе координат

XT.дYT.дZT.д .

Зная координаты точки Q , через нее проводим нормаль Nд к поверхности Tд заменяющего тора. Урав-

нение нормали удобно получить, используя свойство векторного произведения двух векторов, а именно век-

торов, касательных к координатным линиям на поверхности Tд . Для этого уравнения поверхности Tд										запи-
шем в виде:
		(rT.д cos T.д RT.д) cos T.д
r			(r	cos	T.д	R		) sin		(9.68)
r	T.д		T.д	r	T.д	T.д			T.д .	(9.68)
	T.д			r		sin	T.д
				T.д			T.д
						1
						1

Продифференцировав это уравнение по параметрам T.д и T.д , получим:

rT.д

T.д

rT.д sin T.д cos T.д
	r	sin	T.д	sin
	T.д		T.д		T.д
	rT.д cos T.д
		1
		1

		(rT.д cos T.д RT.д) sin T.д
r	T.д		(r	cos		R	) cos
	T.д		T.д		T.д	T.д		T.д	.
T.д									.
T.д						0
						1
						1

На основании приведенных производных уравнения касательных	rT.д	и	rT.д	к координатным лини-
	T.д
			T.д
ям на поверхности Tд можно записать так:

556

9. Топология формообразованных поверхностей деталей

rT.д

[ r

sin

T.д

cos

T.д

sin

T.д

sin

T.д

cos

T.д

;

T.д

rT.д

[ (r

cos

) sin

cos

) cos

T.д

где iT.д ,

jT.д , k T.д – орты системы координат XT.дYT.дZT.д

С учетом рис. 9.12 приведенные зависимости приводят к

rT.д

iT.д

jT.д

k T.д

sin

T.д

cos

T.д

sin

T.д

sin

T.д

cos

T.д

cos

T.д

) sin

T.д

cos

T.д

) cos

T.д

Раскрывая этот определитель, имеем в виду, что в рассматриваемом случае интерес представляет только направление контактной нормали Nд и , а не ее длина; поэтому во второй строке определителя можно при-

нять радиус rT.д	равным единице (т.е. допустимо считать, что rT.д 1). Это соответствует единичной каса-
тельной к координатной линии T.д на поверхности заменяющего тора Tд . По тем же соображениям третью
строку можно сократить на (rT.д cos T.д RT.д ) 0 . В результате получаем, что:
(9.69)	N д и iT.д cos T.д cos T.д jT.д cos T.д sin T.д k T.д sin T.д .

По значениям координат XQ , YQ и ZQ точки Q (они расчитываются по формулам (67)) и по направлению (69) контактной нормали Nд и , записываем уравнение прямой линии r h , вдоль которой измеряется ре-

зультирующая погрешность формообразования h .

Уравнение проходящей через точку Q ( XQ , YQ , ZQ ) прямой r h имеет вид

(9.70)

rQ iT.д XQ jT.дYQ k T.дZQ .

Уравнение прямой, проходящей параллельно направляющему вектору Nд и (69), в векторной форме за-

писывается так:

(9.71)

r h rQ N д иth ,

где th

– параметр текущей точки на прямой r h .

Исходя из (70) и (71) имеем

(9.72)

r h ( XQ th cos T.д cos T.д) iT.д (YQ th cos T.д sin T.д) jT.д (ZQ th sin T.д) k T.д .

A (RT.д rТ.д) (RT.и rТ.и)

Чтобы

установить координаты точки P

(см.

рис. 9.13) пересечения прямой r h

с поверхностью тора

Tд ,

ZT.д

ZT.и

достаточно рассмотреть уравнение (72) совместно с

коор-

уравнением поверхности Tи , записанным в системе

XT.д

XT.и

динат XT.дYT.дZT.д .

Как следует из рис. 9.12,

система координат

YT.и

XT.иYT.иZT.и

заменяющего тора

Tи смещена

вдоль

YT.д

Рис. 9.15. Относительное

расположение

систем

координат

заменяю-

щих торов Т

и Т .

557

оси XT.д системы координат XT.дYT.дZT.д

заменяющего тора Tд

на величину

A (RT.д rT.д ) (RT.и rT.и )

и развернута вокруг этой оси на угол относительной локальной ориентации

поверхностей

и И

(рис. 9.15). Поэтому опе-ратор результирующего перехода от системы координат

XT.иYT.иZT.и

к системе

координат X Y

может быть представлен так Rs T T

T.д

, Tr A, 0, 0 или:

T.д T.д

T.д

Rs T T

cos

sin

cos

Умножим столбцовую матрицу (68) слева на оператор Rs Tи Tд

преобразования координат – полу-

чим матрицу [rT.д](д)

поверхности заменяющего тора rT.д , записанную в системе координат XT.дYT.дZT.д :

(rT.и cos T.и

RT.и ) cos T.и A

]

Rs T T

cos

T.и

) sin

T.и

cos r

sin

T.и

sin

T.д

(д)

T.и

cos

T.и

) sin

T.и

sin r

sin

T.и

cos

T.и

или в векторной форме:

r	(д) i	T.д	r	cos	T.и	R	cos	T.и	A
	T.и	T.д	T.и		T.и	T.и		T.и
	jT.д rT.и cos T.и RT.и sin T.и cos rT.и sin T.и sin									(9.73)
	k T.д rT.и cos T.и RT.и sin T.и sin rT.и sin T.и cos .

В точке пересечения прямой r h (72) и поверхности rT(д.и) (73) координаты их общей точки одни и те же,

поэтому должны выполняться очевидные соотношения:
XQ th cos T.д cos T.д (rT.и cos T.и RT.и ) cos T.и A;
YQ th cos T.д sin T.д (rT.и cos T.и RT.и ) sin T.и cos rT.и sin T.и sin ;		(9.74)
ZQ th sin T.д (rT.и cos T.и RT.и ) sin T.и sin rT.и sin T.и cos .
Таким образом по трем уравнениям (74) определяются три неизвестных параметра и , и		и th , которые
задают положение точки P пересечения поверхности заменяющего тора Tи с прямой (71).
При этом возможны следующие два варианта.
1-й вариант: если простыми средствами удается определить параметр th	для точки P ,	то подставляя
найденное значение этого параметра в (72), сразу находим координаты XP , YP	и ZP точки	P . Если пара-

метр th определить сложно, то для нахождения координат точки P следует использавать

558	9. Топология формообразованных поверхностей деталей

2-й вариант: из уравнений (74) для точки P находятся значения параметров и и и , которые затем подставляются в уравнение (73). Таким путем в системе координат тора Tд записывается радиус-вектор точки P , чем и определяются ее координаты.

С учетом найденных значений координат точек Q( XQ , YQ , ZQ ) и P( XP , YP , ZP ) , уточненное значение

результирующей погрешности ~ формообразования поверхности детали, расчитанное без использования h

принципа суперпозиции, равно:

( X

)

2 (Y Y ) 2

) 2 .

P Q

С учетом последнего результата можно утверждать, что принцип суперпозиции элементарных составляющих при расчете результирующей погрешности формообразования поверхностей деталей может быть использован, если выполняется условие:

~	h ,
h h	h ,
где h – допуск на точность определения погрешности		~
где h – допуск на точность определения погрешности		h .

Наиболее точный результат будет получен, если вместо заменяющих торов использовать собственно поверхности Д и И.

ЗАКЛЮЧЕНИЕ

В монографии изложены основы дифференциально-геометрического метода формообразования поверхностей деталей – нового направления в теории формообразования поверхностей при механической обработке деталей. Этот метод развит исходя из постулированной концепции, в соответствие с которой при разработке технологии механической обработки первичной является обрабатываемая поверхность детали, а вся необходимая дополнительная информация может быть вычислена по данным о геометрии обрабатываемой поверхности с учетом требований к точности ее формообразования.

Однозначное аналитическое описание (синтез) наивыгоднейшей исходной инструментальной поверхности в функции обрабатываемой поверхности детали (как ее -отображение) и аналитическое описание (синтез) наивыгоднейшей кинематики формообразования в функции поверхности детали и исходной инструментальной поверхности дает основание утверждать, что в соответствие с разработанным методом весь процесс наивыгоднейшего формообразования может быть полностью описан (синтезирован) в функции только формообразуемой поверхности детали. Этим подтверждена правильность исходной концепции выполненного исследования и принципиально решена задача синтеза наивыгоднейшего формообразования поверхностей деталей.

Дифференциально-геометрический метод формообразования обладает рядом принципиально важных преимуществ. В частности, его применение позволяет отказаться от повсеместного использования консервативного подхода, сводящегося к назначению большинства параметров процесса обработки исходя только из накопленного практического опыта и использовать вместо этого результаты аналитического решения задачи синтеза1 наивыгоднейшего формообразования поверхности детали. Вместе с тем полностью игнорировать имеющийся практический опыт не следует.

Разработанный метод эффективен при комплексном подходе к решению задач синтеза наивыгоднейшего формообразования сложных поверхностей деталей на многокоординатных станках с ЧПУ и деталей общемашиностроительного назначения на соответствующем оборудовании. В теории этого метода многое удалось достичь путем применения метода подвижного трехгранника (подвижного репера), внутренним образом связанного с поверхностью Д детали и с исходной инструментальной поверхностью И . Если задаться вопросом о

внутренних причинах плодотворности разработанного метода формообразования поверхностей деталей, нужно прежде всего обратить внимание на то, что он предполагает широкое использование методов дифференциальной геометрии двумерного E2 и трехмерного E3 евклидова пространства, представляющей собой обширную

область приложения анализа бесконечно малых (дифференциального и интегрального исчисления, а также элементов теории дифференциальных уравнений) к исследованию геометрических образов деталей и инструментов. Использованный аппарат дифференциальной геометрии можно рассматривать как приложение анализа к теории формообразования поверхностей при механической обработке деталей, а сама теория формообразования в значительной мере может быть представлена как геометрическая интерпретация элементов теории дифференциальных уравнений с частными производными.

Предметом разработанного метода является процесс формообразования заданной поверхности детали. Этот процесс рассматривается сначала в малом – вблизи (в дифференциальной окрестности) текущей точки касания поверхности детали и исходной инструментальной поверхности. Аналитически описав таким образом

1Здесь полезно еще раз остановиться на принципиальном различии задач синтеза и задач оптимизации в том смысле, как это понимается в настоящей монографии. В результате решения задачи синтеза создается новое техническое решение, являющееся наивыгоднейшим для конкретных условий обработки. Это решение может быть синтезировано с учетом ограничений на величины параметров синтезируемого технического решения. Результатом же решения задачи оптимизации является оптимальное сочетание параметров исходного технического решения, структура которого заранее известна. При этом исходное решение может иметь принципиальные недостатки, неустранимые в результате решения задачи оптимизации. Именно такая принципиальная разница усматривается между задачами синтеза и оптимизации в данной монографии. Детально со спецификой задач оптимизации в машиностроениии можно познакомиться по книге

Seireg, A.A., Rodriguez, J., (1997).

<<< < Предыдущая 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 5556 / 6056 57 58 59 60 > Следующая >>>

Соседние файлы в предмете Технология машиностроения

#
23.02.202324.47 Mб12Radzevich, S.P. Monograph - 2001.pdf
#
23.02.20237.23 Mб4Горбацевич - Курсовое проектирование по ТМ.doc
#
23.02.2023949.47 Кб3Мешкова - Организация Технологии Отрасли.pdf
#
23.02.20234.4 Mб1Оптимизация Технологических Систем (укр).pdf
#
23.02.2023882.47 Кб3Основные Положения Теории Базирования (Лекции).pdf
#
23.02.20231.01 Mб7Основы Проектирования ТП.pdf