21. Теоремы подобия. Первая теорема Ньютона и ее доказательство. Вторая и третья теоремы подобия. Пи – теорема Бэкингема.

I теорема сформулирована Ньютоном:

При подобии систем всегда могут быть найдены такие безразмерные комплексы величин, которые для сходственных точек данных систем одинаковы, т. е. подобные явления характеризуются численно равными критериями подобия. Доказательство теоремы рассмотрим, применив закон движения тел (II закон Ньютона) к промышленному объекту и его модели.

Для промышленного образца:

, (3.10)

Для его модели:

= , (3.11)

По условию подобия физические величины модели могут быть выражены через величины образца с помощью констант подобия:

, , , , (3.12)

Выразим переменные модели через изменение промышленного образца и подставим в уравнение Ньютона (3.11) записанное для модели: (3.13) 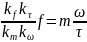(3.14)

Полученное уравнение (3.14) тождественно уравнению II закона Ньютона, записанного для промышленного образца: (3.15)

Подставляя в уравнение (3.15):

; ; ; константы подобия по уравнениям (3.12) получаем выражение:

, (3.16)

Полученное выражение (3.16) разделяем по индексам и получаем уравнение, обе части которого представляют комплекс:

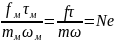, (3.17)

Безразмерный комплекс представляет собой критерий Ньютона. Этот критерий характеризует отношение силы, действующей на частицу к силе инерции.

II теорема была доказана Бэкингемом, Федерманом, Афанасьевым-Эренфест:

Решение любого дифференциально уравнения, связывающего между собой переменные, влияющее на процесс, может быть представлено в виде зависимости между безразмерными комплексами этих величин, т.е. между критериями подобия.

Если ; … критерии подобия, то решение любого дифференциального уравнения, описывающего процесс может быть получено в виде

, (3.18)

Такие уравнения называют уравнением в обобщенных переменных или критериальными уравнениями.

Вторая теорема подобия отвечает на вопрос, как обрабатывать результаты опытов, проведенных на моделях: их надо представить в виде функциональной зависимости между критериями подобия.

СледствиеII теоремы.

Всякое уравнение, связывающее между собой «n» физических величин, среди которых «m» величин обладают независимыми размерностями, может быть преобразовано к уравнению, связывающему (n–m) безразмерных комплексов и симплексов, составленных из этих величин.

III теорема Кирпичева-Гухмана формулирует необходимые и достаточные условия подобия явлений: подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и у которых соблюдается подобие условий однозначности, т. е. явления подобны, если их определяющие критерии равны.

22. Теория подобия и ее применение к исследованию процессов перемещения жидкостей и газов.

Метод анализа размерностей

Этот метод применяется, если рассматриваемый процесс очень сложен и для него затруднительно составить дифференциальное уравнение.

Базируется он на двух допущениях:

1. Известно (из опытов) от каких параметров процесса и изменений зависит рассматриваемая величина, т.е.

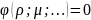
2. Связь между существенными для исследуемого процесса физическими величинами выражается в виде степенного многочлена.

Для установления числа критериев, которыми может быть описан процесс используем II теорему Бэкингэма.

Для примера рассмотрим процесс движения жидкости по трубопроводу. Нам необходимо знать как различные физические факторы влияют на гидравлическое сопротивление трубопровода. Пусть из предварительных опытов известно, что сопротивление трубопровода будет зависеть от физических характеристик продукта (ρ) и (μ), геометрических характеристик трубопровода (d) и (l), а также от скорости движения жидкости (ω) и для вертикального трубопровода оказывает влияние сила тяжести. Её влияние учтём введя в функциональную зависимость(g).

, (3.19)

n=7

, = , ,l=m, d=m, g= , m=3, m=4

Результат будет представлен в виде функции зависимости:

Подставим размерности входящих величин:

, (3.20)

Сгруппируем члены с одинаковым основанием:

Составим систему, исходя из одинаковости размерностей левой части и правой:

Примем за известные величины y, k, n. Получим:

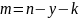
Найденные значения подставим в уравнение (2):

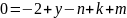
, (3.21)

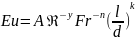
, (3.22)

В полученном критериальном уравнении число критериев – 4, причем один из них (l/d) является симплексом геометрического подобия:

1. Критерий Эйлера: 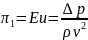, (3.23)

Характеризует соотношение между силами давления и силами инерции, т.к. в критерий Эйлера входит искомая величина Δp.

2. Критерий Рейнольдса: ,(3.24)

Характеризует соотношение между силами инерции и вязкостного трения.

3. Критерий Фруда: , (3.25)

Характеризует соотношение сил инерции и сил тяжести.

4. Симплекс геометрического подобия: , (3.26)

Характеризует соотношение геометрических величин в подобных системах.

Критерий Eu– определяемый, а критерии Re, Fr, Г определяющие. Тогда полученное уравнение может быть записано в виде:

, (3.27)