28. Свойства гидростатического давления. Доказательство независимости величины давления от ориентации площадки в пространстве.

Гидростатическое давление обладает двумя основными свойствами.

1-ое свойство. Силы гидростатического давления в покоящейся жидкости всегда направлены внутрь по нормали к площадке действия, т.е. являются сжимающими.

Это свойство доказывается от противного. Если предположить, что силы направлены по нормали наружу, то это равносильно появлению в жидкости растягивающих напряжений, которых она воспринимать не может (это вытекает из свойств жидкости).

2-ое свойство. Величина гидростатического давления в любой точке жидкости по всем на­правлениям одинаково, т.е. не зависит от ориентации в пространстве площадки, на которую оно действует

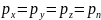
где   - гидростатические давления по направлению координатных осей;

 - то же по произвольному направлению n.

Для доказательства этого свойства выделим в неподвижной жидкости элементарный объем в форме тетраэдра с ребрами, параллельными координатным осям и соответственно равными  , dy и dz (рис. 2.3).

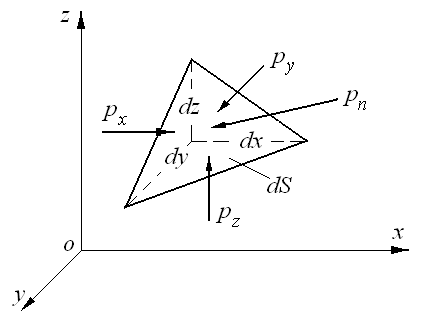
Рис. 2.3. Схема для доказательства свойства о независимости гидростатического давления от направления

Введем обозначения:   - гидростатическое давление, действующее на грань, нормальную к оси Ox;

 - давление на грань, нормальную к оси Oy;

 - давление на грань, нормальную к оси Oz;

 - давление, действующее на наклонную грань;

dS - площадь этой грани;

ρ - плотность жидкости.

Запишем условия равновесия для тетраэдра (как для твердого тела) в виде трех уравнений проекций сил и трех уравнений моментов:

При уменьшении в пределе объема тетраэдра до нуля система действующих сил преобразуется в систему сил, проходящих через одну точку, и, таким образом, уравнения моментов теряют смысл.

Таким образом, внутри выделенного объема на жидкость действует единичная массовая сила, проекции ускорений которой равны X, Y, и Z. В гидравлике принято массовые силы относить к единице массы, а так как G=mg, то проекция единичной массовой силы численно будет равна ускорению.

где  ,  ,   - проекции единичной массовой силы на оси координат;

m - масса жидкости;

g - ускорение.

Составим уравнение равновесия выделенного объема жидкости в направлении оси Ox, учитывая при этом, что все силы направлены по нормалям к соответствующим площадкам внутрь объема жидкости:

(2.4)

Где   - проекция силы от гидростатического давления  ;

- проекция силы от давления  ;

 - проекция массовой силы, действующей на тетраэдр.

Разделив уравнение (2.2) на площадь , которая равна пло­щади проекции наклонной грани dS на плоскость yOz, т. е.   получим

При стремлении размеров тетраэдра к нулю последний член уравнения, содержащий множитель dx, также стремится к нулю , а давления   и   остаются величинами конечными.

Следовательно, в пределе получим

Или

Аналогично составляя уравнения равновесия вдоль осей Oy и Oz, находим

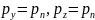
Или

Так как размеры тетраэдра dx, dy и dz и наклон площадки dS взяты произвольно, то, следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаково. Что и требовалось доказать.

Рассмотренное свойство давления в неподвижной жидкости имеет место также при движении невязкой (идеальной) жидкости. При движении же реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством, строго говоря, не обладает.

В общем случае давление в точке зависит от координат рассматриваемой точки, а при неустановившемся движении жидкости может изменяться в каждой данной точке с течением времени: