49 Дифференциальные уравнения движения реальных жидкостей (уравнения Навье-Стокса). Критерии гидродинамического подобия.

Рассмотрим случай движения реальной (вязкой) жидкости. При ее движении в потоке помимо сил гидродинамического давления P будут возникать и силы вязкостного трения Т. Их действие проявляется в возникновении касательных напряжений , которые определяются из закона внутреннего трения Ньютона.

Если движение жидкости рассматривать как плоское одномерное (вдоль одной из осей, например OX см. рисунок 8.3), тогда величина скорости будет зависить только от расстояния z до горизонтальной плоскости отсчета.

Р исунок 8.3 − К определению величины касательных напряжений

В этих условиях возникающие касательные напряжения зависят от градиента скорости , который может определяться из условия подобия треугольников скоростей

Выделим в потоке равномерно движущейся реальной жидкости элементарный объем с размерами ребер . Рассмотрим плоское движение жидкости вдоль оси OX. В выделенном элементарном объеме будут действовать поверхностные силы: силы давления Р и трения Т, а также массовые силы М.

Согласно основному принципу динамики, запишем уравнение равновесия:

Р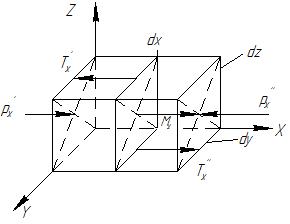 исунок 8.4 − К выводу уравнения Навье − Стокса

Силы трения представим через возникающие от их действия касательные напряжения и как:

и

Как следует из расчетной схемы, касательные напряжения возникают лишь на поверхности верхней и нижней граней выделенного параллелепипеда. Площадь поверхности граней будет равна .

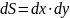Выразим касательные напряжения через касательные напряжения, действующие на нижней грани . Производная выражает изменение касательных напряжений вдоль вертикального ребра в точках, лежащих на нижней грани параллелепипеда, а ( )·dz выражает изменение этого напряжения вдоль всей длины dz ребра параллелепипеда.

Тогда силы трения выразится как:

и

Равнодействующая сил трения будет равна:

Подставляя , получим:

В более общем случае (трехмерное движение) составляющая скорости будет изменяться не только в направлении оси Z, но и в направлении всех трех осей координат. Тогда проекция равнодействующей сил трения на ось X примет вид:

сумму вторых производных по осям координат называют оператором Лапласа

Следовательно, равнодействующая сил трения в проекции на ось X:

На ось Y:

На ось Z

Проекции на оси координат всех сил (тяжести, давления и трения), действующих на элементарный объем капельной жидкости составляют :

Вдоль оси X

Вдоль оси Y

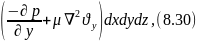
Вдоль оси Z

Суммы проекций сил на оси координат, в соответствии с основным принципом динамики, должны быть равны произведению массы жидкости , заключенной в элементарном объеме, на проекции ускорения на соответствующие оси координат. Поэтому система уравнений (8.29) − (8.31) приобретает вид:

Субстанциональные произведения ; ; выражаются аналогично как и при выводе уравнения Эйлера:

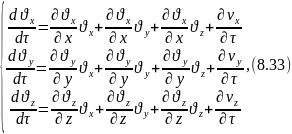
Системы уравнений (8.32) и (8.33) представляет собой уравнения Навье- Стокса, описывающие движение вязкой капельной жидкости.