53. Расчет расхода жидкости при ламинарном режиме движения (уравнение Пуазейля).

В ламинарном потоке жидкости выделим элементарное кольцевое сечение расположенное на расстоянии r от оси круглой трубы. Толщина кольца равна dr.

Рисунок 10.3- К выводу уравнения Пуазейля.

Площадь этого кольца будет равна

(10.9)

Но при dr0 величина будет представлять собой бесконечно малую величину и в дальнейшем рассматриваться не будет. В таком случае

(10.10)

Объемный расход жидкости через это кольцевое сечение будет равен

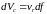_(10.11)

где v_r – скорость движения жидкости. Из закона Стокса она определяется как

тогда секундный расход жидкости будет равен

(10.12)

Интегрируя, полученное уравнение в пределах изменения r от 0 (по оси трубы) до R (стенка трубы), получим общий расход жидкости через все живое сечение

(10.13)

Определяя интегралы и приводя подобные, получим

(10.14)

если R=d/2, то

(10.15)

Уравнение (10.15) носит название уравнение Пуазейля и позволяет рассчитать расход жидкости при ламинарном режиме течения.

54. Течение жидкости в малом зазоре. Уравнение Петрова.

С оздателем гидродинамической теории смазки является профессор Н. П. Петров. До него считали, что в подшипниках скольжения происходит трение одного тела (вала) о другое (вкладыш). Н. П. Петров показал, что при вращении вал увлекает за собой смазочную жидкость, направляя ее в зазор между валом и вкладышем в нижней части (рис. 6.11, а). От этого давление в зазоре между валом и вкладышем возрастает. Образуется своего рода масляный клин, вытесняющий вал вверх и влево (рис. 6.11, б). При увеличении числа оборотов п вал "всплывает". Таким образом, трения вала о вкладыш не происходит – сухое трение заменяется жидкостным. При увеличении числа оборотов вал стремится встать в центре отверстия во вкладыше (центр вала О1 совпадает с центром подшипника О – рис. 6.11, в).

Вывод формулы Петрова для силы трения основывается на следующем. При одинаковой толщине слоя смазки

где и – окружная скорость. При радиусе вата r и длине вкладыша l (рис. 6.11, г) полная поверхность, по которой происходит трение:

Тогда сила трения будет

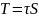
Так как то

Отсюда

Учитывая, что

где – угловая скорость; п – число оборотов вала, получаем

55. Турбулентный поток и его структура. Интенсивность пульсаций и турбулентная вязкость потока. Закон распределения скорости по сечению потока

Турбулентный режим движения

Так как при Re> 2300 происходит смена ламинарного режима на турбулентный, то можно сделать вывод, что закономерности турбулентного движения отличаются от закономерностей ламинарного режима. Проблема турбулентного режима возникла в середине в. в результате противоречия между теоретическим (казалось бы, вполне строгим выводом закона сопротивления в круглой трубе из уравнения Навье – Стокса) и эмпирическими законами сопротивления. Это противоречие выходило далеко за пределы ошибок измерений. Первый закон (Пуазейля) давал сопротивление, пропорциональное 1-й степени скорости; второй закон (Шези) приводил к квадрату скорости.

Теоретический анализ турбулентного движения, являющегося, на первый взгляд, совершенно беспорядочным, представляет большие трудности. Однако, несмотря на беспорядочность движения отдельных частиц в турбулентном потоке, в целом имеет место свой строгий порядок, свои вполне определенные закономерности, которые будут рассмотрены ниже.