
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf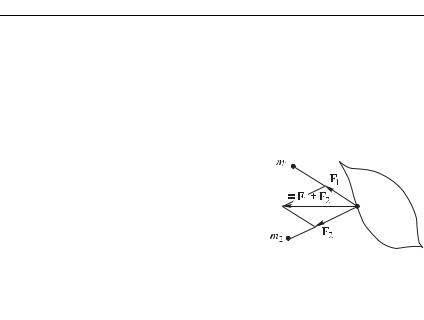
5.2 ] |
Потенциальная энергия. Закон сохранения энергии |
81 |
|||
пути, а зависит только от начального и конечного положения |
|||||
этой материальной точки. |
|
|
|
||
Представим себе теперь, что на заданную материальную точ- |
|||||
ку действуют силы со стороны ! других материальных точек, |
|||||
причем все эти силы 1, 2, F |
являются центральными. |
||||
Результирующая сила, действующая на заданную материальную |
|||||
точку уже не является центральной — в разных точках простран- |
|||||
ства она не будет направлена к какому либо одному и тому же |
|||||
центру (для наглядности на рис. 5.6 |
|
1 |
|
||
изображен случай, когда на матери- |
|
|
|||
|
|
|
|||
альную |
точку массы |
действуют |
|
|
à |
две центральные силы гравитационно- |
Fð |
|
|||
m |
|
||||
го притяжения со стороны двух мате- |
|
|
|||
|
|
|
|||
риальных точек с массами 1 и 2). |
|
á |
|
||
Для |
дальнейших |
рассуждений |
|
|
2 |
воспользуемся тем фактом, что ре- |
Рис. 5.6 |
|
|||
зультирующая сила р равна вектор- |
|
||||
|
|
|
|||
ной сумме составляющих ее сил 1, 2, ... |
. Это заранее |
||||
не очевидное свойство сил получило название принципа |
|||||
суперпозиции сил. Следовательно справедливо соотношение: |
|
||||
р , |
(5.16) |
1
итогда элементарная работа при перемещении материальной точки на величину при действии результирующей силы р
может быть записана согласно определению (5.2) в виде
Æр р |
Æ , |
(5.17) |
1 |
1 |
|
где Æ — элементарная работа, совершаемая центральной силой. Отсюда для полной работы р результирующей силы при перемещении из некоторой точки 1 в точку 2 получаем
|
2 |
2 |
|
|
|
|
|
1 |
|
1 |
(5.18) |
р |
|
р |
1 2 |
||
|
1 |
1 |
|
|
|
Каждая из работ 1, 2, совершается центральной силой и поэтому не зависит от пути. Следовательно и работа р не зависит от пути.
Вернемся к определению потенциальной энергии (5.13):
, 0
Так как работа не зависит от пути, то после выбора какого-либо нулевого положения 0 потенциальная энергия однозначно зави-
82 |
Работа и энергия |
[ Гл. 5 |
сит только от положения материальной точки в пространстве. Что касается выбора нулевого положения, то этот выбор определяется соображениями удобства решения конкретной механической задачи.
Произвол в выборе нулевого положения приводит к тому, что
потенциальная энергия определена с точностью до произвольной константы. В самом деле, вычтем из потенциальной энер-
гии при одном выборе начального положения , 0 потенциальную энергию при другом выборе начального положения , 0 :
, , 0 0 |
(5.19) |
Так как работа не зависит от пути, то справедливо соотношение
0 0 0 0
Подставляя это равенство в (5.19), получаем
, , 0 0 ,
то есть изменение нулевого положения действительно приводит к изменению потенциальной энергии на величину 0 0 , не зависящую от — положения материальной точки в простран-
стве.
Сумма кинетической и потенциальной энергий называется полной энергией материальной точки и обозначается обычно
буквой -:
- , |
(5.20) |
Покажем, что при движении материальной точки в поле консервативных сил или, что то же, в потенциальном поле ее
полная энергия не меняется. Для этого воспользуемся соотношением, связывающим бесконечно малое изменение кинетической энергии с работой:
Æ |
(5.21) |
Это равенство справедливо для движения под действием любой силы, а не только потенциальной. Но лишь в этом последнем случае его правую часть можно выразить через изменение потенциальной энергии:
, , (5.22) |
|
0 |
0 |
Так как работа в случае потенциальной силы не зависит от пути, то
0 0
С учетом этого равенства соотношение (5.22) можно записать
в виде
Æ

5.2 ] Потенциальная энергия. Закон сохранения энергии 83
Подставляя полученный результат в (5.21), приходим к равенству
, , 0, 0
Дифференциал (бесконечно малое приращение) любой функции равен нулю, если эта функция является константой, то есть мы получили
- , |
(5.23) |
Это соотношение выражает закон сохранения энергии. Укажем еще одно весьма полезное формальное следствие ра-
венства (5.22). Предположим вначале ради упрощения выкладок, что либо потенциальная энергия зависит только от одной координаты, либо движение происходит лишь вдоль одной координаты. В обоих этих случаях можем положить , , Соответственно, в элементе работы Æ существенна лишь компонента силы
(с учетом ее знака). Положив Æ |
, получаем |
|
|
|
(5.24) |
|
|
|
В качестве примера приведем выражение для потенциальной энергии деформированной пружины. При малых деформациях связь между силой и смещением, как известно, линейна:, что соответствует квадратичной зависимости для потенциальной энергии: , 2 2
В принципе ту же операцию мы можем провести и в общем трехмерном случае. Рассматривая малые перемещения вдоль осей , , , мы получим три дополняющих друг друга соотношения:
|
|
, |
, |
|
|
|
, |
, |
|||||
|
, |
|
|
Входящие в них производные по одной координате при фиксированных остальных называются в математике частными производными и обозначаются через . . и т. д. Таким образом, вектор силы F в компонентах может быть представлен следующим образом:
|
, |
, |
|
(5.25) |
|
|
|
|
|
Эти соотношения имеют более общий характер, нежели сама ньютонова механика. В практическом отношении они удобны для вычисления силы, если известна потенциальная энергия как функция координат.
Соотношения (5.25) можно представить в компактной форме, введя формально вектор
1 2 3 ,
84 |
Работа и энергия |
[ Гл. 5 |
который в математике называется градиентом. Мы еще неоднократно встретимся с такими операторами в разделе «Электричество и магнетизм». Такой формализм позволяет переписать (5.25)
впредельно коротком виде:
,
5.3.О законе сохранения энергии
инепотенциальных силах
Вэлементарных курсах физики закон сохранения энергии (5.23) зачастую толкуется упрощенно. Мы попытаемся в данном параграфе дать о нем более адекватное представление.
Прежде всего заметим, что, сколь бы ни естественным казалось предположение о центральном характере сил взаимодействия между двумя материальными точками, оно отнюдь не универсально. Например, взаимодействие между двумя электронами, движущимися с непараллельными скоростями, к потенциальным силам не сводится. Поэтому и примеры наши с центральными силами (а они всегда потенциальны) — это именно примеры, но не доказательство.
Эксперимент — основа любой естественной науки — показы-
вает, что все многообразие силовых полей в рамках механики подразделяется на три класса. Помимо консервативных сил, нам придется рассмотреть еще гироскопические и диссипативные.
Гироскопическими называются силы, работа которых всегда в точности равна нулю. Очевидно, 0 при 0, если
, а поскольку , то это означает . Примеров таких сил можно привести немного, наиболее очевидным является случай силы Лоренца, которая действует на частицу с зарядом / в магнитном поле :
/
Эти силы, как следует из самого определения, ни к потенциальной
энергии, ни к закону сохранения энергии отношения не имеют. Диссипативными называются силы, работа которых пони-
жает энергию - , (диссипация — затухание, рассеяние энергии). Это силы трения, знакомые нам из школьного курса; к диссипативным относятся также силы вязкого сопротивления жидкости или газа (они-то и не дают парашютисту падать с ускорением ), сила радиационного торможения при ускорении заряженных частиц и многие другие. Этим классом сил обу-
словлено то обстоятельство, что закон сохранения энергии (5.23)
в рамках одной только механики оказывается верным лишь приблизительно, с большей или меньшей точностью.

5.3 ] |
О законе сохранения энергии и непотенциальных силах |
85 |
|
|
В принципе, полная энергия - механической системы может |
||
даже расти во времени. Это просто означает, что наша система |
|||
не достаточно хорошо изолирована от других тел, и над ней |
|||
совершается работа извне. По этой причине точность закона |
|||
(5.23) не может быть выше той точности, с которой мы можем |
|||
считать законы движения не зависящими от внешнего мира. |
|
||
|
Но как бы тщательно мы не изолировали механическую си- |
||
стему, сколь бы скрупулезно ни учитывали количественно вли- |
|||
яние внешней среды, мы никогда не сможем выполнить условие |
|||
(5.23) с любой наперед заданной точностью, причем изменение |
|||
полной энергии будет происходить именно в сторону потерь. Это |
|||
означает, что вступает в игру диссипация, и предельная точность |
|||
закона (5.23) определяется именно уровнем диссипации. Обычно |
|||
при этом говорят: «Энергия сохраняется, но переходит в другие |
|||
виды», но что такое эти «другие виды», нам еще предстоит |
|||
разбираться на протяжении всего нашего курса. |
|
|
|
|
Мы рассмотрим пример сил трения между твердыми телами |
||
как наиболее хрестоматийный. Популярный образ зацепляющих- |
|||
ся неровностей на поверхности соприкасающихся тел не дает |
|||
правильного понимания природы явления, ибо сам механизм |
|||
зацепления остается как бы «за скобками». В действительности |
|||
в основе сил трения лежит электромагнитное взаимодействие |
|||
электронных оболочек атомов и молекул. Феноменологические |
|||
законы (т. е. законы, обобщающие напрямую опытные данные) |
|||
представляют собой усредненные и огрубленные количествен- |
|||
ные соотношения. Сформулируем их для случая сухого трения |
|||
скольжения. Этим термином называют трение между поверх- |
|||
ностями двух твердых тел, скользящих друг по другу при от- |
|||
сутствии между ними какой-либо прослойки, например смазки. |
|||
В случае сухого трения сила трения возникает не только при |
|||
скольжении одной поверхности по другой, но и при попытках |
|||
вызвать такое скольжение у покоящегося вначале тела. В по- |
|||
следнем случае она называется силой трения покоя. Рассмотрим |
|||
два соприкасающихся тела 1 и 2, причем тело 2 закреплено |
|||
неподвижно (рис. 5.7). Пусть тело 1 прижи- |
|
|
|
мается к телу 2 с силой , направленной |
|
|
|
по нормали к поверхности соприкоснове- |
|
|
|
ния тел. Она называется силой нормаль- |
1 N |
F |
|
ного давления. Она может быть обуслов- |
|
||
лена притяжением первого тела к Земле |
|
|
|
(силой тяжести) или другими причинами. |
2 |
|
|
Если тело 1 (вместе с телом 2) в инер- |
|
|
|
циальной системе отсчета не перемещается |
Рис. 5.7 |
|
|
в вертикальном направлении и его ускоре- |
|
|
|
ние в этом направлении равно нулю, то это означает согласно |
|||
второму закону Ньютона, что на него со стороны второго тела |
|||

86 Работа и энергия [ Гл. 5
действует уравновешивающая сила, равная по модулю и направленная вверх. Ее называют силой реакции опоры и обычно
обозначают через N. По своему происхождению она аналогична упругой силе и также обусловлена электромагнитным взаимодействием молекул в поверхностных областях тела 1 и тела 2.
Если попытаться переместить первое тело, подействовав на него внешней горизонтальной силой , то обнаружится, что для каждой конкретной пары тел и каждого значения силы нормального давления имеется определенное минимальное по модулю значение 0 силы , при котором тело 1 удается сдвинуть с места. При значениях внешней силы, заключенных в пределах 0 ' ' 0, тело остается в покое. По второму закону Ньютона это возможно только в том случае, когда сила уравновешивается равной ей и противоположно направленной силой, которая и есть сила трения покоя тр (см. рис. 5.7). Эта сила, действующая на тело 1 со стороны тела 2, по модулю равна величине внешней силы до тех пор, пока последняя не превосходит наибольшего значения силы трения покоя 0. Из опыта следует, что во многих практически интересных ситуациях сила 0 оказывается пропорциональна нормальному давлению : 0 #0 .
Когда внешняя сила превзойдет по модулю 0, тело начнет скользить, причем до некоторого значения скорости проскальзывания движение будет равномерным. При этом, как следует из второго закона Ньютона, сила трения должна быть равна по модулю составляющей приложенной силы, параллельной соприкасающимся поверхностям, и полностью ее уравновешивать. Отсутствие у тела ускорения означает, что скорость проскальзывания зависит от приложенной силы, и притом нередко весьма сложным образом.
Увеличивая приложенную силу , мы в конце концов превзойдем предельную силу трения скольжения, и далее движе-
ние будет происходить уже с ускорением |
|
тр; тр # , |
(5.26) |
причем при специальной обработке соприкасающихся поверхностей сила трения скольжения может оказаться практически не зависящей от скорости движения тела и, что особенно интересно — от площади соприкосновения трущихся тел. Разумеется, эти свойства не являются ни вполне точными, ни вполне универсальными, но все же правильно описывают большой массив
экспериментальных данных. Безразмерный коэффициент пропорциональности называется коэффициентом трения (соответ-
ственно покоя #0 или скольжения #). Он зависит от природы и состояния трущихся поверхностей, в частности от их шероховатости. Коэффициенты трения покоя и скольжения практически никогда не совпадают друг с другом.
5.3 ] |
О законе сохранения энергии и непотенциальных силах |
87 |
|
Попробуем проанализировать эту ситуацию с точки зрения |
|
закона сохранения энергии. Из (5.26) легко усмотреть, что работа силы уже не равна приращению кинетической энергии тела
2 2 Часть ее, равная работе силы трения тр |
, как бы |
«исчезает» — это и есть диссипация. |
|
Еще выразительнее проявляются диссипативные |
эффекты |
при тр ' — работа совершается, но кинетическая энергия не изменяется.
Энергия, соответствующая работе сил трения, переходит к атомам поверхности — увеличивается их кинетическая энергия. Это увеличение кинетической энергии атомов находит свое отражение в повышении температуры трущихся поверхностей. (Подробнее о связи хаотического движения атомов вещества с его тепловыми свойствами будет рассказано в одном из последующих разделов курса — термодинамике). Поэтому говорят, что «потерянная» из-за трения кинетическая энергия переходит в тепло. Она может переходить также в акустические возбуждения, электромагнитные волны и даже радиоактивные излучения, но сути дела это не меняет.
Получим формальное соотношение, определяющее изменение полной энергии материальной точки из-за действия на нее неконсервативных сил. Для этого воспользуемся соотношением (5.9), связывающим бесконечно малое изменение кинетической энергии с работой:
к н Æк н,
где к обозначает результирующую всех консервативных сил, ан — результирующую всех неконсервативных сил. Пусть тело совершает конечное перемещение по некоторой траектории из точки 1 в точку 2. Тогда бесконечно малые изменения в полученных соотношениях следует просуммировать вдоль этого участка траектории:
22
Æн, или -2 -1 н 1 2
11
Итак: при действии на материальную точку неконсервативных сил изменение ее полной энергии на любом участке траектории равно работе на этом участке результирующей неконсервативных сил. В частности, работа сил трения скольжения всегда отрицательна, так как они всегда направлены против перемещения тела, поэтому силы трения всегда приводят к уменьшению полной механической энергии движущегося тела.
Таким образом, когда мы говорим, что в изолированной системе энергия сохраняется, это означает, что энергия может переходить из одной формы в другую, но ее количество остается
88 |
Работа и энергия |
[ Гл. 5 |
постоянным, оно не зависит от времени. Закон сохранения энергии является строгим законом природы, справедливым для всех известных взаимодействий.
5.4. Простые примеры
Закон сохранения энергии — не только фундаментальный закон природы, но и эффективный метод решения задач. В этом
отношении полезны любые законы сохранения (как принято называть их в механике — интегралы движения), и принцип их
использования совершенно универсален — не решая уравнений движения (например, не вычисляя траекторию материальной точки), сразу же связать начальное и конечное состояния системы. Именно по такому принципу мы выводили формулу Циолковского из закона сохранения импульса.
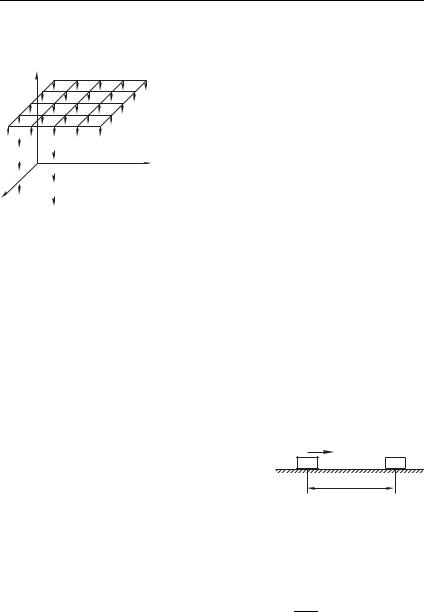
Начнем с движения материальной точки под действием силы тяжести. Чтобы использовать закон сохранения энергии для исследования движения, необходимо сначала определить конкретное выражение для потенциальной энергии, то есть найти ее зависимость от положения тела в пространстве. Для этого необходимо выбрать в пространстве некоторую произвольную точку с радиусом-вектором 0 и вычислить работу, совершаемую
силой тяжести при перемещении ма-
|
|
z |
|
|
|
|
|
|
|
|
|
|
териальной точки с массой из |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
заданного положения в положе- |
|
|
|
|
r |
|
|
|
|
A |
|
mgz |
ние 0. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y |
|
|
|
z |
|
|
y |
Чтобы сделать изложенную вы- |
|
|
|
O |
|
|
|
|
|
|
|
ше процедуру более наглядной, вос- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
|
|
r0 |
|
|
|
|
|
|
|
|
пользуемся рис. 5.8. На этом рисун- |
x |
|
|
|
|
|
|
|
|
|
|
|
ке положение материальной точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
A 0 |
с массой определяется ее радиу- |
||||||||
U A(r r0 ) A |
|
|
|
A mgz |
сом-вектором r в декартовой систе- |
||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ме координат , у которой плос- |
Рис. 5.8 |
кость совпадает с поверхностью |
|
Земли. Для определения потенциальной энергии выберем точку с радиусом-вектором 0 в любом месте на поверхности Земли. Работу силы тяжести при перемещении из точки в точку 0, которая, как мы знаем, не зависит от пути, вычислим вдоль пути, состоящего из двух отрезков: вдоль вертикали до поверхности и далее вдоль произвольной траектории по поверхности до точки с радиусом-вектором 0. На первом участке работа равна произведению модуля силы тяжести на величину пути до поверхности Земли, т. е. на координату нашей материальной точки. А на втором участке работа равна нулю, так как здесь сила всюду перпендикулярна перемещению. Таким образом, работа силы тяжести при перемещении материальной

5.4 ] |
Простые примеры |
89 |
|
точки из положения |
с |
радиусом-вектором r |
в положение |
с радиусом-вектором |
0, |
то есть потенциальная энергия, |
|
,
Следовательно, закон сохранения энергии при движении материальной точки под действием только силы тяжести имеет вид следующего соотношения, справедливого для любой точки траектории:
- 2 |
|
(5.27) |
2 |
|
|
Если, например, тело начинает падать с некоторой высоты0 с нулевой начальной скоростью, то из закона сохранения энергии (5.27) легко получить закон нарастания скорости по мере приближения тела к поверхности:
0 |
2 |
|
2 0 |
|
2 |
||||
|
|
|
Определим выражение для потенциальной энергии и для второго простейшего типа движения материальной точки, рассмотренного в предыдущей главе, — для гармонических колебаний груза по поверхности под действием упругой силы со стороны пружины (см. рисунки 4.5, 4.6). В качестве произвольного начального положения с радиусом-вектором 0 в определении потенциальной энергии используем равновесное положение груза при 0. Тогда потенциальная энергия в положении равна работе упругой силы при перемещении материальной точки из положения с координатой в положение c координатой0: , 2 2 Таким образом, закон сохранения полной энергии при гармонических колебаниях материальной точки по поверхности записывается в виде
2 |
2 |
|
(5.28) |
2 |
2 |
|
|
С помощью этого соотношения можно решать многие задачи о гармонических колебаниях, не прибегая к интегрированию уравнений движения. Так например, если нам задана начальная скорость груза 0 в положении равновесия 0, то из (5.28) легко найти амплитуду 0 возникающих после этого гармонических колебаний. При максимальном отклонении скорость груза, а следовательно и его кинетическая энергия равны нулю. Применяя (5.28) к начальному моменту времени и к моменту, когда достигается максимальное отклонение, получаем
2 |
2 |
|
|
|
|
|
|
|
|
||
0 |
0 |
, |
0 0 |
|
|
2 |
2 |
|
|
|
|
Особо подчеркнем, что закон сохранения энергии при движении во внешнем силовом поле справедлив только при движении
90 |
|
Работа и энергия |
|
|
[ Гл. 5 |
||
материальной точки под действием сил, постоянных во времени. |
|||||||
(В противном случае условие (5.12) не было бы инвариантно |
|||||||
по отношению к выбору траектории ). О таком движении |
|||||||
|
|
говорят иногда, как о движении в по- |
|||||
z |
|
стоянном силовом поле, понимая под |
|||||
|
|
словом |
«поле» |
пространство, |
каждой |
||
|
mg |
точке |
которого |
соответствует |
вектор |
||
|
|
действующей |
в |
пространстве |
силы. |
||
|
mg |
(На рис. 5.9 в качестве примера изоб- |
|||||
|
y ражено постоянное силовое поле силы |
||||||
|
|
тяжести). Если условие постоянства |
|||||
x |
mg |
силового поля не выполняется, полная |
|||||
|
энергия материальной точки, |
вообще |
|||||
|
|
||||||
|
Рис. 5.9 |
говоря, не сохраняется. С одним из та- |
|||||
|
ких примеров мы имели дело в преды- |
||||||
дущей главе, когда рассматривали явление резонанса, возникаю- |
|||||||
щего при колебаниях тела, на которое помимо упругой силы дей- |
|||||||
ствует еще внешняя вынуждающая сила. Полная энергия в этом |
|||||||
случае растет с ростом амплитуды вынужденных колебаний. |
|||||||
Полезно рассмотреть также пример, когда для решения зада- |
|||||||
чи используется не сохранение энергии, а ее полная диссипация. |
|||||||
Это также нередко дает возможность получить простой ответ, не |
|||||||
решая уравнений движения. |
|
|
|
|
|||
Уменьшение энергии, обусловленное действием сил трения, |
|||||||
можно определить с помощью соотношения между изменением |
|||||||
кинетической энергии и работой (5.11), которое часто оказыва- |
|||||||
ется полезным при решении задач. В качестве наглядного при- |
|||||||
мера рассмотрим такую задачу (рис. 5.10). На горизонтальной |
|||||||
поверхности лежит тело массы , ко- |
|
v0 |
|
||||
торому в начальный момент сообща- |
|
|
|||||
ют скорость поступательного движе- |
|
|
|
||||
ния 0. Из-за трения |
о |
поверхность |
|
l |
|
||
тело |
останавливается |
на |
некотором |
|
|
|
|
расстоянии от исходного положения. |
|
Рис. 5.10 |
|
||||
Чему равно это расстояние, если коэф- |
|
|
|||||
|
|
|
|||||
фициент трения равен #? Ответ можно, конечно, найти путем |
|||||||
решения соответствующего уравнения движения (второго закона |
|||||||
Ньютона). Но решение можно проще и короче получить с помо- |
|||||||
щью соотношения (5.11), из которого сразу получаем |
|
||||||
2 |
|
2 |
|
||
0 |
тр # , |
|
0 |
|
|
2 |
|||||
|
2 |
|
|||
Конечно, результат этот приблизителен, а иногда может быть и просто неверен, поскольку мы воспользовались приближением постоянной силы трения. Но принцип решения подобных задач наш пример демонстрирует должным образом.
