
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
6.4 ] Закон всемирного тяготения 111
Таково выражение для второй космической скорости. Из срав-
нения с (6.29) видно, что вторая космическая скорость в 2 раз больше первой: 22 11 км/c.
Для того чтобы навсегда покинуть Солнечную систему, тело должно преодолеть, помимо земного притяжения, еще и силы притяжения к Солнцу. Необходимая для этого скорость 23 существенно зависит от направления запуска, поскольку скорость Земли на орбите сравнима с искомой величиной: 23 30 км/с. При запуске в направлении орбитального движения Земли эта
скорость минимальна и составляет около 17 км/c. Она называется третьей космической скоростью.
Применяя к различным ситуациям закон всемирного тяготения (6.25), мы оставили открытым вопрос, до какой степени мы вправе это делать, если в реальной задаче фигурируют далеко не точечные массы. Ни в формуле (6.29), ни в левой части формулы (6.30) Земля отнюдь не может быть представлена как материальная точка. В действительности мы молчаливо подразумевали, что сферически симметричное распределение массы может рассматриваться («глядя извне») как материальная точка. Покажем, что это действительно так.
Итак, нашей задачей является определение модуля и направления силы гравитационного притяжения, действующей между Землей (с массой ) и материальной точкой (с массой ), которая находится на расстоянии от центра Земли (рис. 6.9 a).
Сделаем два упрощающих предпо- |
m |
m |
||
ложения. Во-первых, будем считать |
||||
|
|
|||
Землю строго сферическим телом, |
|
|
||
хотя она слегка сплющена вдоль |
M |
|
||
своей оси вращения. Во-вторых, бу- |
|
|
||
дем предполагать, что |
плотность |
|
R |
|
вещества Земли всюду |
постоянна. |
|
||
|
|
|||
Оба эти предположения выполня- |
|
|
||
ются с хорошей точностью — до- |
à |
á |
||
статочно сказать, что силы тяжести |
|
|
||
измеренные на полюсе и на эквато- |
Рис. 6.9 |
|
ре отличаются на доли процента. Это означает, что наша задача сводится к определению силы гравитационного притяжения между материальной точкой и однородным шаром (рис. 6.9 б).
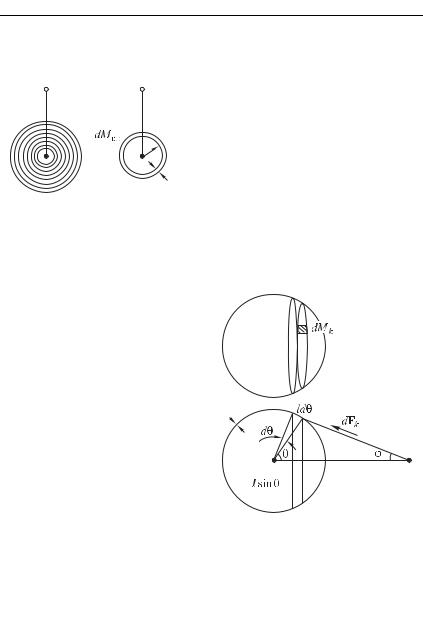
Представим нашу Землю в виде совокупности материальных точек — бесконечно малых объемов с массой , притом каждый из них взаимодействует с материальной точкой с известной силой тяготения , величина и направление которой определяются их взаимным расположением (рис. 6.9 б). Результирующая сила притяжения со стороны шара определится затем векторной суммой всех этих элементарных сил .
112 |
|
Замкнутая система тел |
[ Гл. 6 |
||
При вычислении результирующей силы мы используем сим- |
|||||
метрию задачи. А именно, представим сплошной шар как со- |
|||||
вокупность |
тонких шаровых слоев, |
вложенных друг в |
друга |
||
|
m |
m |
(рис. 6.10 а), и вычислим |
снача- |
|
|
ла силу притяжения между исход- |
||||
|
|
|
|||
|
r |
r |
ной материальной точкой и одним |
||
|
|
|
из шаровых слоев, радиус которо- |
||
M |
|
l |
го обозначим через , толщину — |
||
|
|
|
через |
, а массу — через |
сл |
|
|
dl |
(рис. 6.10 б). |
|
|
|
|
|
Для нахождения силы взаимо- |
||
|
à |
á |
действия между слоем и матери- |
||
|
Рис. 6.10 |
альной точкой выделим сначала из |
|||
|
слоя кольцо, края которого отвеча- |
||||
|
|
|
|||
ют значениям угла и |
(рис. 6.11 а). На рис. 6.11 б кольцо |
||||
обозначено штриховыми линиями. Каждый бесконечно малый |
|||||
элемент кольца с массой |
находится на одном и том же рас- |
||||
стоянии от массы и по- |
|
|
|
||
этому действует на эту массу |
|
|
|
||
с силой всемирного тяготе- |
|
|
|
||
ния |
, которая по модулю |
|
|
|
|
одинакова |
для всех малых |
à |
|
|
|
элементов кольца и равна |
|
|
|
||
|
|
|
|
|
(6.32) |
|
|
|
|
|||
|
|
5 |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
d |
|
|
|||||
Из |
симметрии |
задачи |
ясно, |
|
l |
|
|
|||||
|
l |
|
|
|||||||||
что при вычислении суммар- |
|
|
|
|||||||||
|
|
a |
|
|||||||||
ной |
силы |
со стороны |
все- |
|
|
|
m |
|||||
го |
кольца |
следует |
учесть |
á |
{ |
r |
||||||
|
||||||||||||
только |
вклад |
от |
|
|
|
|
|
|||||
|
|
— составляющей |
|
|
|
|||||||
силы |
вдоль прямой, со- |
|
|
|
|
|||||||
единяющей массу с цен- |
|
Рис. 6.11 |
|
|
||||||||
тром шарового слоя. Вклады |
|
|
|
|||||||||
|
|
|
|
|||||||||
от перпендикулярных к этому направлению составляющих |
|
|||||||||||
взаимно уничтожатся при их суммировании от всех элементов |
||||||||||||
кольца |
. |
|
|
|
|
|
|
|
|
|||
Итак, сила , действующая на массу со стороны одного |
||||||||||||
кольца, направлена к центру шарового слоя и по модулю равна |
||||||||||||
с учетом (6.32) |
|
|
|
|
|
|
|
|||||
кол |
|
|
|
|
|
|
5 2 |
|
5 |
2 , |
|
|
по кольцу |
|
по кольцу |
|
(6.33) |
где |
— масса |
кольца. Выражение для |
мы |
найдем, |
|

6.4 ] Закон всемирного тяготения 113
если учтем, что радиус кольца равен , а ширина — (рис. 6.11 б). Следовательно, площадь кольца определяется выражением 2$ 2 . Если толщина шарового слоя , а плотность 3, то масса кольца, равная произведению его объема на плотность, составляет
2$ 2 3 2$32
Подставляя это выражение в (6.33), получаем |
|
|
кол 5 2$32 $ $ |
|
(6.34) |
2 |
|
|
Весь рассматриваемый нами шаровой слой можно представить, как совокупность колец, положение которых однозначно задаетcя углом (при заданных и величины и однозначно зависят от ). Поэтому суммарная сила сл со стороны всего слоя определяется суммой вкладов (6.34) от всех колец:
сл кол 5 2$32 $ $ |
|
(6.35) |
|
по всем кольцам |
2 |
|
|
|
|
|
|
В (6.35) удобно перейти от интегрирования по к интегрированию по всем возможным расстояниям . Для этого воспользуемся известной из тригонометрии теоремой косинусов (см. рис. 6.11 б):
2 2 2 2 , |
2 2 2 2 |
(6.36) |
|||
Продифференцировав первое из этих соотношений (при по- |
|||||
стоянных и ), получаем |
|
|
|
|
|
|
2 |
2 |
|
(6.37) |
|
Определив |
из (6.37) и из (6.36), получим после |
||||
подстановки результатов в (6.35) |
|
|
|
||
|
|
|
2 #2 2 |
|
|
сл 5 % |
, |
(6.38) |
|||
|
|
#2 |
2 |
|
|
|
|
|
|
|
|
где мы учли, что может изменяться в пределах от до
.
Интеграл в (6.38) разбивается на сумму двух интегралов
|
|
|
|
|
2 2 |
|
2 |
|
|
|
|

114 Замкнутая система тел [ Гл. 6
Нетрудно убедиться, что после интегрирования для обоих слагаемых получается одинаковый результат, а именно, 2 . Поэтому получаем из (6.38)
% |
|
4 2 |
|
|
сл 5 |
|
# |
2 |
|
|
|
|
|
|
Выражение 4$ 2 дает объем слоя, а 3 4$ 2 — его массу cл. Таким образом, находим окончательно, что шаровой слой с массой сл действует на находящуюся вне слоя материаль-
ную точку с массой с силой, направленной к центру слоя и равной по модулю:
сл 5 |
сл |
, |
(6.39) |
|
#2 |
||||
|
|
|
где — расстояние от точечной массы до центра слоя. Любопытно отметить, что если точечная масса находится внутри шарового слоя, то действующая на нее результирующая сила со стороны всего слоя равна нулю. В этом легко убедиться, изменив в (6.38) пределы интегрирования по от значения до, которые соответствуют нахождению массы внутри слоя.
Просуммировав выражение (6.39) по всем слоям, получим силу, с которой шар притягивает массу ,
сл 5 |
|
|
|
# |
2 |
5 #2 |
|
|
|
|
|
Таким образом, действие шара на материальную точку эквивалентно действию помещенной в центре шара материальной точки с массой, равной массе шара.
6.5. Упругие и неупругие соударения
Обратимся к изучению круга явлений, которые, в зависимости от области физики, именуются столкновениями, соударениями, рассеянием. Преимущественно процессы такого рода
важны в физике микромира (едва ли не главная задача в физике элементарных частиц — задача о рассеянии). Столкновения составляют один из важнейших предметов рассмотрения в физической кинетике, т. е. в молекулярной физике, физике плазмы, растворов и т. д. Но и в небесной механике, коль скоро речь идет не о регулярных планетных или звездных системах, но об астероидах, кометах, фрагментах, образовавшихся как следствие
взрывных процессов, данная проблема занимает достойное место. Главная особенность взаимодействий, которые могут быть
квалифицированы как столкновения, состоит в следующем. Участвующие в них частицы (тела) как бы «приходят из бесконечности» и в конечном состоянии «уходят на бесконечность»,

6.5 ] Упругие и неупругие соударения 115
где взаимодействием можно пренебречь. Сразу ясно, например, что взаимодействие Земли и Солнца не может быть отнесено к этой категории. А вот соударение биллиардных шаров — в принципе, может, хотя о бесконечностях в пределах биллиардного стола говорить и не принято. Но при достаточной и вполне разумной степени идеализации задачи (пренебрежение трением о сукно, тем более — обменом импульса через воз-
мущение воздуха или гравитационным взаимодействием шаров) можно утверждать, что шары взаимодействуют в процессе удара,
но не взаимодействуют до или после него. Значительно сложнее представить таким образом столкновение заряженных частиц, взаимодействующих по закону Кулона, поскольку сила и потенциальная энергия их взаимодействия не обращаются в нуль ни на каком конечном расстоянии. Отсюда и возникает бесконечность в корректном определении процесса столкновения, а в реальной ситуации мы всегда имеем дело с некоторым приближением к таковому.
Мы в рамках курса механики ограничимся достаточно простыми примерами, по преимуществу такими, когда при соударении тела приходят в непосредственный контакт друг с другом. Термин «соударение» как раз и относят обычно к классической механике макроскопических тел. В этом случае определение траекторий тел после соударения путем решения уравнений движения оказывается часто очень сложной, а иногда вообще невыполнимой задачей. Вот тут-то особенно полезными оказываются законы сохранения энергии и импульса, применение которых к задачам о соударениях мы сейчас рассмотрим.
При соударении макроскопические тела деформируются. При этом некоторая часть кинетической энергии, которой обладали тела перед ударом, переходит в потенциальную энергию упругой деформации, а некоторая часть кинетической энергии переходит во внутреннюю энергию образующих тела атомов и молекул. В зависимости от того, насколько меняется внутренняя энергия тел, при решении задач используют нередко одно из двух при-
ближений: абсолютно упругий и абсолютно неупругий удар. Абсолютно упругим ударом называют такое соударение тел,
при котором переходом части их энергии во внутреннюю энергию тел можно пренебречь. Можно считать, что при таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела восстанавливают свою форму, отталкивая друг друга. В результате потенциальная энергия упругой деформации переходит обратно в кинетическую энергию, и тела разлетаются со скоростями, величина и направление которых определяется двумя условиями —
законом сохранения полной энергии и законом сохранения полного импульса сталкивающихся тел. При абсолютно неупругом

116 Замкнутая система тел [ Гл. 6
ударе тела «слипаются», т. е. после удара они движутся с одинаковой скоростью либо покоятся. Кинетическая энергия тел полностью или частично превращается в их внутреннюю энергию. Кинетическая энергия тел до и после соударения имеет различное значение, и выполняется лишь закон сохранения импульса.
z |
|
|
|
|
|
|
|
Пример абсолютно неупругого |
||
y m |
m2 |
m1 m2 |
удара показан на рис. 6.12. |
|||||||
|
||||||||||
|
Рассмотрим также |
пример |
||||||||
|
1 v1 |
v2 0 |
|
v x |
||||||
O |
|
|
|
|
|
|
|
абсолютно упругого удара, при- |
||
|
|
|
|
|
|
|
||||
|
|
|
v m1v1/(m1 m2 ) |
чем ограничимся случаем цен- |
||||||
|
|
|
Рис. 6.12 |
|
|
|
|
трального удара двух однород- |
||
|
|
|
|
|
|
|
ных шаров, один из |
которых |
||
|
|
|
|
|
|
|
|
|||
первоначально покоится. (Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры.) Пусть вращение шаров отсутствует и пусть справедливо приближение, в котором два тела образуют как бы замкнутую систему, или, что то же, внешние силы, приложенные к шарам, уравновешивают друг друга (как, например, при скольжении шаров без трения по горизонтальной поверхности). Обозначим
массы шаров через 1 и 2. |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть второй шар до удара |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неподвижен, а первый до удара |
|
|
y m1 v |
|
|
m |
|
|
v1 |
v |
|
|
||||||
двигался в положительном на- |
|
|
|
|
|
|
10 |
|
2 |
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
правлении оси со скоростью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
v m1 m2 |
v |
|
v |
|
|
2m1 |
v |
|
|
|
||||||
10 (рис. 6.13). Скорости шаров |
1 |
m1 |
m2 |
|
10 |
2 |
|
|
m1 m2 |
|
10 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
после удара обозначим через 1 |
|
|
|
|
|
|
|
Рис. 6.13 |
|
|
|
|
|
|
|
|
||
и 2. Эти неизвестные пока величины являются проекциями на ось соответствующих векто-
ров 1 и 2, и, следовательно, их знак, полученный в результате решения, определит, в каком направлении оси шары будут двигаться после удара.
Запишем условия сохранения энергии и импульса:
2 |
2 |
2 |
|
|
|||
|
1 10 |
1 1 |
2 2 |
, |
(6.40) |
||
|
2 |
|
2 |
2 |
|||
|
(6.41) |
||||||
1 10 1 1 2 2 |
|||||||
Решение системы уравнений (6.40), (6.41) — задача элементарная. Искомые значения для 1 и 2:
1 |
2 |
10, 2 |
2 1 |
, |
(6.42) |
|
1 |
|
|
10 |
|||
|
2 |
|||||
1 |
|
1 2 |
|
|
||
Отметим некоторые особенности движения шаров при их упругом центральном ударе, вытекающие из полученного решения (6.42). Если массы шаров равны, то из (6.42) следует, что1 0, 2 10. Это означает, что в таком случае первый шар после удара останавливается, а второй движется с той скоро-
6.5 ] |
Упругие и неупругие соударения |
117 |
стью, которая была у первого шара до удара. Именно по этой причине наилучшей защитой от быстрых нейтронов оказываются вещества, содержащие как можно больше водорода. При столкновении нейтрона с ядром атома водорода — протоном — последний перехватывает практически всю кинетическую энергию (поскольку p n), а нейтрон останавливается.
Рассмотрим случай упругого столкновения тела со стенкой, т. е. с телом, массу которого можно считать бесконечно большой.
Для этого случая из (6.42) получаем 1 10, 2 0, т. е. в результате упругого столкновения со стенкой первый шар меняет
свою скорость на противоположную, отскакивая от стенки с той же по модулю скоростью, с которой он к стенке подлетал. Если же столкновение происходит с движущейся стенкой (которая в принципе моделирует любое массивное тело), то весь этот сценарий просто переносится в систему отсчета движущейся стенки. Возвращаясь в лабораторную систему, получаем
2 20 ; 1 10 2 20, |
(6.43) |
в предположении, что 10, 20 считаются однонаправленными (направления «вперед-назад» учитываются посредством знака). Подчеркнем, что соударение, упругое в системе отсчета стенки, безусловно остается таковым и в л-системе: при корректном подсчете кинетической энергии уже нельзя пренебрегать поправками к 1, 2 порядка 1 2 в формуле (6.43).
Пусть теперь рассматривается упругое столкновение двух частиц, которое уже не может быть описано в рамках одномерной модели. Припишем индекс начальным значениям всех физических величин, а индекс 7 — конечным. Закон сохранения импульса в произвольной системе отсчета будет существенно трехмерным:
|
|
|
, |
(6.44) |
1 |
2 |
1 |
2 |
|
где p — сохраняющийся суммарный импульс системы сталкивающихся частиц. В ц-системе 0, и размерность уравнения (6.44) понижается. Действительно, векторы 1 2 определяют некоторую прямую, векторы 1 2 — еще одну прямую, а две пересекающиеся прямые задают некоторую плоскость (исключая тот вырожденный случай, когда 1 1 , так что задача оказывается одномерной). Следовательно, в ц-системе процесс рассеяния всегда происходит в некоторой плоскости, поэтому в общем случае вместо двух переменных 1, 2 в уравнениях (6.40), (6.41), мы будем иметь дело с четырьмя. Процесс рассеяния, ввиду его фактической двумерности, удобно представить графически, как это показано на рис. 6.14.
В ц-системе 1 2 8 , тогда кинетическая энергия в ц-системе (которая при упругом столкновении сохраняется)
118 Замкнутая система тел [ Гл. 6
равна |
&2 |
1 |
|
1 |
|
|
&2 |
1 |
|
1 |
|
|
|||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
2 1 |
2 |
2 1 |
2 |
||||||||||||
|
|
|
|
|
|||||||||||
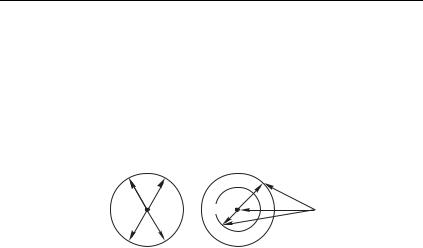
Отсюда следует, что и после соударения 1 2 8 . Таким образом, концы векторов 1 , , 2 в ц-системе можно представить лежащими на окружности, как это показано на рис. 6.14 а: в результате рассеяния векторы 1,2 поворачиваются, как показано на рисунке, не изменяя своей длины (модуля). Похожая картинка получилась бы и для скоростей частиц,
p1 f |
p1i |
|
|
v1C |
v1 |
|
v2C |
VC |
|
v2 |
|
|
|
|
p2i |
p2 f |
|
à |
á |
|
|
Рис. 6.14 |
|
только концы векторов 1,2 располагались бы на концентрических окружностях с радиусами, соответственно равными 8 1, 8 2 На рис. 6.14 б показано, как можно построить векторы скорости частиц в л-системе, складывая 1,2 с вектором скорости центра масс. Такое построение можно провести и для начальных, и для конечных скоростей.
Если бы столкновение было неупругим, но мы бы знали, какая именно доля кинетической энергии в ц-системе утрачена, можно было бы провести аналогичное построение, но радиус соответствующих окружностей был бы разным для начального и конечного состояний. Эта проблема — учет неупругости с известными потерями — чрезвычайно важна в контексте молекулярной, атомной и ядерной физики, ибо моделирует реакции — от химических до ядерных.
Вопросы и задачи
1.Что такое приведенная масса?
2.Что такое энергия взаимодействия трех материальных точек?
3.Напишите выражение для энергии гравитационного взаимодействия двух материальных точек с массами 1 и 2.
4.Как связана сила взаимодействия между двумя материальными точками
сих энергией взаимодействия?
5.Что такое центр масс?
6.Чем отличаются упругие соударения от неупругих?
7.Что такое первая, вторая и третья космические скорости?
8.Определить долю энергии Æ, теряемую частицей массы 1 при упругом центральном столкновении с неподвижной частицей массы 2. При каком соотношении масс 1 2 потеря энергии максимальна? Используя полученный

6.6 ] Вопросы и задачи 119
результат, объяснить, почему в ядерных реакторах для замедления нейтронов используется рассеяние их на ядрах атомов легких (дейтерий, углерод), а не
тяжелых элементов.
Ответ: Æ 4 1 2 1 2 2. Отсюда видно, что при 1 2 теряется вся энергия (Æ 1).
9. Лодка длиной и массы с находящимся на ее корме человеком массы неподвижно стоит на спокойной воде носом у причала перпендикулярно ему. На сколько отодвинется лодка от причала, когда человек пройдет по лодке
с кормы на нос?
Ответ:
10. На дне маленькой запаянной пробирки, подвешенной над столом на нити, сидит муха, масса которой равна массе пробирки. Расстояние от дна пробирки до стола равно длине пробирки . Нить пережигают, и за время падения муха перелетает со дна в верхний конец пробирки. Определите время падения пробирки.
Ответ:
11. Два маятника в виде шариков разных масс 1 и 2 подвешены на нитях разной длины 1 и 2 так, что шарики соприкасаются. Первый шарик отводят в плоскости нитей на небольшой угол ' и отпускают. На какие углы
отклонятся маятники после упругого удара?
Ответ: '1 ' 1 2 1 2 , '2 2'1 1 2 1 2
12. Тело, движущееся со скоростью , догоняет стенку, движущуюся в том же направлении со скоростью " . Найдите скорость тела после упругого
соударения.
Ответ: 2" .
13. Шайба массы , скользя по льду, сталкивается с неподвижной шайбой массы 3 . Считая удар центральным и упругим, определите, на каком расстоянии ( друг от друга остановятся шайбы, если скорость первой шайбы непосредственно перед ударом была равна , а коэффициент трения между шайбами и льдом равен .
Ответ: ( 2 4 .
Г л а в а 7
УРАВНЕНИЕ МОМЕНТОВ. ДИНАМИКА ТВЕРДОГО ТЕЛА
7.1. Момент импульса и момент силы
Введем два понятия, чрезвычайно важных для описания движения (и как частный случай — равновесия) макроскопического твердого тела. Но вводить их целесообразно на основе закона движения материальной точки:
|
|
(7.1) |
|
|
|||
|
|
В векторной форме уравнение (7.1) имеет универсальный вид во всех инерциальных системах отсчета и не зависит от выбора начала координат. Предположим, что мы выбрали в качестве такового некоторую точку . Пусть r — радиус-вектор нашей материальной точки в системе координат с началом в точке . Проведем некоторую тождественную операцию — умножим все уравнение (7.1) слева векторно на r:
|
|
|
|
|
|||
|
|
Учтем, далее, что
L |
P |
= |
|
h
O 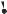
для материальной |
точки |
, |
|
|||||
Отсюда следует, в частности, что |
||||||||
mv |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
, |
|
|
|
|
||||||
|
|
|
|
|
|
|
||
так что в целом второй закон Ньютона (7.1) приводится к эквивалентному виду
|
, |
(7.2) |
|
|
|||
|
|
где векторная величина именуется моментом силы F относительно точки , а , соответственно, моментом импульса материальной точки относительно точки — (рис. 7.1).
В плоскости, заданной векторами r и p, модуль вектора L может быть представлен, в соответствии с рис. 7.1, как
+ 8 # .
Пусть, например, материальная точка массы движется по окружности радиуса (рис. 7.2). Момент импульса этой
