
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
3.4 ] Электродвижущая сила. Правила Кирхгофа 241
приводит и другого рода соображение: ввиду неизбежной, хотя бы и сколь угодно слабой, диссипации, источник тока должен совершать работу.
Таким образом, постоянный ток не может рассматриваться иначе, как удобное приближение, адекватность которого обеспечивается сильным неравенством >, где — характерный временной масштаб задачи, а > — характерное время релаксации источника.
Для решения электротехнических задач, связанных с рассмотрением квазиодномерных цепей, подобных изображенной на рис. 3.2 а, немецким физиком Густавом Р. Кирхгофом (1824– 1887) были предложены специальные приемы, базирующиеся на фундаментальных физических законах. Собственно цепь на рис. 3.2 а ни в каких иных рецептах, кроме закона Ома, не нуждается. Необходимость в дополнительных формальных правилах возникает при рассмотрении разветвленных цепей.
Первое правило Кирхгофа относится именно к точкам разветвления или узлам (рис. 3.2 б). Из стационарности задачи следует, в частности, что в узловой точке не должен накапливаться заряд. Это значит, что заряд, поступающий в единицу времени в эту точку, должен быть равен заряду, уносимому из нее в единицу времени. Конкретно, для случая рис. 3.2 б должно быть :1 :2 :3 Общий рецепт строится по тому же принципу.
Будем считать, ради удобства, ток, втекающий в узел, положительным, а ток, из него вытекающий, — отрицательным. Тогда для любого узла сложной схемы должно иметь место
соотношение |
|
|
|
: 0 |
(3.17) |
Это и есть первое правило Кирхгофа.
Для иллюстрации второго правила Кирхгофа обратимся к рис. 3.2 в. Любой замкнутый контур, который мы произвольным образом выделили бы из этой разветвленной схемы, должен был бы удовлетворить условию (3.16). Интеграл от потенциального поля по замкнутому контуру дал бы нуль, а фактически эта операция даст алгебраическую сумму всех ЭДС, включенных в контур. Но в случае системы с соредоточенными параметрами (3.16) можно существенно упростить, заменив интеграл просто суммой по элементам контура:
: , |
(3.18) |
|
|
|
|
где как токи : , так и ЭДС выбираются с учетом знака — по
соотношению направления тока и направления обхода контура. В этом состоит второе правило Кирхгофа. Направления (знаки)
с самого начала можно выбрать произвольно, при последующих
242 |
Постоянный ток |
[ Гл. 3 |
вычислениях они будут исправлены автоматически. Например, для схемы рис. 3.2 в, полагая все токи и ЭДС направленными по часовой стрелке, можем написать
1 2 :1 1 :2 2 : |
|
|
; |
1 :1 1 : ; |
|
|
|
|
:: : 0;
2 2:2 : :
— всего шесть уравнений для всех возможных контуров и еще три уравнения для всех узлов схемы:
:1 : : 0 и т. д.
Обычным свойством оказывается переопределенность системы уравнений, не ведущая, однако, ни к каким парадоксам. Так в нашем примере уравнений получается девять, а неизвестных токов, как следует из рис. 3.2 в, всего пять. При последующей работе с полученными уравнениями из них как раз и получится пять линейно независимых. При расчетах сложных схем правила Кирхгофа дают такие преимущества, что с этой переопределенностью приходится мириться.
Задачи
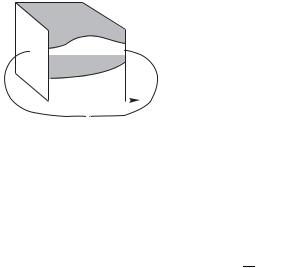
1. Пространство между пластинами плоского конденсатора заполнено многослойным диэлектриком (рис. 3.3), обладающим слабой электропроводностью. Диэлектрическая проницаемость и удельная проводимость изменяются от 01,
|
|
|
|
|
|
|
1 у одной пластины до 02, 2 у другой |
1 |
2 |
|
|
пластины. Конденсатор включен в цепь по- |
|||
|
|
|
|
|
|
|
стоянной ЭДС. Определить величину и знак |
|
|
|
|
|
|
|
суммарного свободного заряда 5, сосредото- |
|
2 |
ченного в объеме диэлектрика, когда в цепи |
|||||
|
1 |
|
|
|
|
|
устанавливается постоянный электрический |
|
2 |
ток +, текущий через диэлектрик по направле- |
|||||
|
1 |
|
|
|
|
|
нию от пластины 1 к пластине 2. |
|
|
|
|
|
x |
Решение. Полезно обратить внимание на |
|
|
|
|
|
|
то, что никаких предположений касательно |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функций 0 , в задаче не сделано. Усло- |
|
|
|
|
|
|
|
вие постоянства тока: |
|
|
|
|
|
|
|
|
|
|
Рис. 3.3 |
+ |
||||
|
|
( 3 * |
|||||
|
|
|
|
|
|
|
|
Отсюда * + ( , тем самым = 00 + ( 0 Соответственно,
% |
|
|
0 |
+ 0 |
|
|
|
|
|
|
|||
|
( |
|||||
Искомая величина получается интегрированием плотности заряда по объему:
2 |
|
|
|
02 |
01 |
|
|
5 ( % 00+ 2 |
|
|
|
1 |
1

3.5 ] Задачи 243
2. Заземление концов телеграфной линии осуществлено посредством ме- |
|||||||||||
таллических шаров радиуса #1 и #2 соответственно (рис. 3.4). Удельная про- |
|||||||||||
водимость грунта вблизи них равна 1 и 2. Найти сопротивление земли |
|||||||||||
между шарами. Считать почву в окрестности каждого из них однородной на |
|||||||||||
расстояниях, больших по сравнению с радиусами |
|
|
|
|
|
|
|
||||
шаров. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
Решение. Для получения сопротивления за- |
|
|
|
~ ~ |
|
|
|
||||
земления в компактной форме полезно прене- |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
бречь также асимметрией, связанной с подводя- |
|
|
|
|
|
|
|
||||
щими проводами. Таким образом, для каждого |
1 |
r1 |
|
2 |
|
||||||
(почти уединенного) шара задача о течении заря- |
|
|
|||||||||
|
|
|
r2 |
||||||||
да оказывается с точностью до малых поправок |
|
|
|
||||||||
сферически симметричной. Отсюда сразу следует: |
|
|
|
|
|
|
|
||||
+ 4#23 # * # |
3 |
|
+ |
|
|
|
|
Рис. 3.4 |
|||
|
4#2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
При вычислении падения напряжения следует учесть, что интеграл * # быстро сходится, поэтому зависимостью # можно пренебречь вдали от электродов, и, кроме того, падения напряжения на двух электродах войдут аддитивно:
|
|
|
|
+ |
+ # |
+ # |
, |
4 1#2 4 2#2 |
|||
1 |
|
2 |
|
откуда и следует
1 1 1
4 1#1 2#2
Всилу сделанных выше предположений, результат представляет собой лишь оценку (впрочем, довольно точную). Но и на оценочном уровне универсальность сопротивления заземления — факт нетривиальный.
3.Определить сопротивление АБ цепочки, изображенной на рис. 3.5 а.
Ответ: АБ 7 5 #.
|
|
|
r |
|
|
|
2r |
|
|
r1 |
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
r2 |
||
A |
|
|
r |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|||
|
|
|
2r |
|
|
|
r |
|
|
|
R |
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
à |
|
|
|
|
|
|
|
á |
|
|||
|
|
|
|
|
|
|
|
|
Рис. 3.5 |
|
|
|
|
||||
4. Два гальванических элемента, ЭДС и внутренние сопротивления которых равны соответственно 1, #1 и 2, #2, соединены параллельно и нагружены на сопротивление (рис. 3.5 б). Определить падение напряжения на сопротивлении .
Ответ: |
1 |
#2 2 |
#1 |
|
|
|
|
#1#2 #1 #2
Г л а в а 4
МАГНИТНОЕ ПОЛЕ ТОКА
4.1. Взаимодействие проводников с током. Понятие о магнитном поле
Говоря о магнитном поле тока, мы подразумеваем, если не оговорено противное, постоянный ток. В действительности, как будет ясно из последующих глав нашего курса, при не слишком жестких ограничениях все результаты настоящей главы могут быть перенесены и на случай переменного тока. Но и те ситуации, когда такой перенос затруднителен, достаточно типичны — это, например, длинные линии или электромагнитные волны в вакууме.
Мы уже упоминали в гл. 3 эффект взаимодействия квазинейтральных токонесущих проводников. В зависимости от величины тока, это взаимодействие может из чисто демонстрационного превратиться в очень сильное, например, результатом его может быть весьма эффектный и небезопасный взрыв соленоида. Цилиндрический проводник с продольным током — лайнер — может при уровне тока в несколько мегаампер создавать при схлопывании на ось давление порядка нескольких тысяч атмосфер.
Задолго до того как был построен первый гальванический элемент, и даже, пожалуй, раньше, чем были осознаны какие-либо электрические явления, человечество познакомилось с постоянными магнитами природного происхождения и, соответственно, с магнитными явлениями. Современная цивилизация сделала подобное знакомство неизбежным для любого ребенка.
Исследование свойств токонесущих проводников привело еще в начале XIX века к пониманию того, что они взаимодействуют не только между собой, но и с постоянными магнитами и взаимодействия эти — одной природы. Так складывалось представление о магнитном поле тока. Именно токовое магнитное поле, а не поле намагниченных образцов, оказалось в конечном счете тем первичным понятием, исходя из которого, мы представляем себе сегодня весь круг магнитных явлений, объединяющихся в современной электродинамике в единое целое с электрическими.
Реальная история физики развивалась таким образом, что первоначальное понимание сути магнетизма оказалось не вполне адекватным. Сначала, была построена, по аналогии с электростатикой, магнитостатика, в которой роль положительных и от-
4.1 ] |
Взаимодействие проводников с током |
245 |
рицательных зарядов исполняли северные и южные магнитные массы (названия были даны исходя из свойств стрелки компаса). Были введены понятия напряженности и индукции магнитного поля. Всю эту иерархию пришлось решительно пересмотреть на основании позднейших данных, и прежде всего — о магнитном поле тока.
Во-первых, оказалось, что магнитных зарядов в принципе нет. Вместо теоремы Гаусса (1.10) или (1.14), магнитное поле, точнее магнитная индукция , подчиняется более простому закону
0, или 0 |
(4.1) |
Таким образом, поток магнитного поля любой природы через любую замкнутую поверхность равен нулю. Традиционная геометрическая интерпретация этого факта такова: силовые линии магнитного поля либо идут из бесконечности в бесконечность, либо замкнуты. (Обращаем особое внимание читателя на неполноту такой классификации — есть еще третья возможность, о которой большинство учебников просто забывает, — см. ниже.)
Во-вторых, как следует из возможности замкнутых силовых линий, магнитное поле и в стационарной задаче не является потенциальным. Можно посмотреть на это свойство и с другой стороны: поскольку теорема Гаусса (4.1) для магнитного поля вырождается, его источники должны фигурировать в каком-то другом уравнении — это будет так называемая теорема о циркуляции.
В § 1.6 мы рассмотрели дипольное приближение в электростатике. В частности, мы пользовались и понятием точечного диполя, но лишь как удобным приближением. Элементарным объектом при этом по умолчанию оставался электрический заряд. Именно заряд оказывается фундаментальным свойством элементарных частиц, тогда как элементарные «точечные» дипольные моменты у них не обнаружены. С точки зрения магнитных свойств элементарным объектом оказывается как раз диполь. У элементарных частиц нет магнитных зарядов, но многие из них обладают собственным магнитным дипольным моментом. (Так называемый магнитный монополь Дирака (по имени английского физика-теоретика П.А.М. Дирака (1902–1984)), входящий в некоторые теоретические построения как гипотетическая частица, в данном контексте рассматриваться не должен. Даже если он и существует реально, свойства его слишком далеко выходят за пределы классической, т. е. неквантовой физики.)
Исторически понятие магнитного диполя, как и многие другие, было введено по полной аналогии с электростатикой. В дальнейшем, когда была признана неадекватность этой аналогии, пришлось изменить и саму методологию построения данного

246 |
Магнитное поле тока |
[ Гл. 4 |
раздела физики, опираясь на взаимодействие проводников с током. Но некоторые «следы» старинной магнитостатики сохранились и в современной электродинамике. Главный из них — так называемая перекрестная аналогия между характеристиками
электрических и магнитных полей.
Суть ее в том, что магнитной индукцией называется векторная силовая характеристика магнитного поля, отражающая взаимодействие поля с током или магнитоактивным веществом
(аналог ).
Напряженностью магнитного поля называется величина, определяемая из конфигурации токов проводимости (или свободных токов) без учета отклика магнитоактивного вещества, или, что то же, микроскопических молекулярных токов (аналог ).
Второе определение с неизбежностью несовершенно — такая же ситуация, как в сегнетоэлектриках, здесь еще более типична. По-настоящему корректное определение напряженности поля можно будет дать лишь на основании уравнений поля и граничных условий (как и для вектора в электростатике).
Очевидно, в вакууме величины и физически тождественны. Но в системе СИ их принято измерять в разных единицах. Коэффициент между единицей — 1 А/м и единицей —
1 Тл (Тесла; по имени сербского ученого Н. Тесла (1856–1943)) называется магнитной постоянной и обозначается символом
10 4$ 10 7 СИ. Единица ее измерения по традиции именуется генри на метр (Г/м). Полезно заранее иметь в виду следующее равенство:
где 3 108 м/с — скорость света. Строгий вывод этой формулы будет дан в главе «Электромагнитные волны».
Таким образом, в вакууме или в веществе, откликом которого на магнитное поле можно пренебречь, имеет место соотношение
10 |
(4.2) |
Соотношение (4.2) открывает цепочку самосогласованных формул, обобщающих опытные данные и корректно вводящих понятие магнитного поля. Для двух последующих законов нам еще понадобится определение элемента тока. Под таковым понимается малый участок квазиодномерного проводника, по которому течет ток :. В последующие формулы он войдет в виде : , где — вектор элемента длины провода, поперечные масштабы которого пренебрежимо малы.
Итак, если электрическое поле действует на заряды как таковые и порождается зарядами, то магнитное поле действует на токи и токами порождается. Именно с вклада элемента тока в создание магнитного поля мы и начнем. Для этого рассмотрим

4.1 ] Взаимодействие проводников с током 247
так называемый закон Био и Савара (по имени французских физиков Ж.Б. Био (1774–1862) и Ф. Савара (1791–1841)):
|
1 |
|
|
, |
(4.3) |
|
4 #3 : |
|
|||||
|
|
|
||||
Для вычисления полного поля формулу (4.3) следует проинтегрировать по . При этом векторное произведение автоматически согласует направление поля с «правилом буравчика».
Взаимодействие элемента тока с внешним магнитным полем описывается законом Ампера (по имени А.М. Ампера
(1775–1836); иногда, быть может, более правильно его называют законом Лапласа по имени французского астронома, физика и
математика П.С. Лапласа (1749–1827)):
: , |
(4.4) |
Полную силу и момент, действующие на проводник, и в этом случае можно получить, интегрируя по . Формулы (4.3) и (4.4) вместе с соотношением (4.2) дают полное описание взаимодействия двух токонесущих проводников через посредство магнитного поля. Поучительна попытка Ампера объединить две основных формулы в одну:
|
|
: |
|
|
, |
|
|
!0 |
|
+1+2 |
|
, |
|
|
(4.5) |
|
|
12 |
|
1 |
|
1 |
2 |
|
4 |
|
#123 |
|
1 |
2 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Раскрывая двойное векторное произведение по известной формуле
,
получаем
|
|
, |
|
2 |
|
, |
|
12 |
, |
|
|
1 |
2 |
12 |
|
1 |
12 |
|
1 |
2 |
|
Попробуем в этой формуле поменять местами индексы 1 и 2. Лишь второй член остается без изменений (с точностью, разумеется, до знака), но не первый. Таким образом,
12 21
Означает ли это, что или неверен третий закон Ньютона, или какая-нибудь из наших формул? Вовсе нет. Дело в том, что соотношения (4.3), (4.4) оперируют лишь с малыми элементами токонесущих проводов и дают в ответе лишь дифференциал вклада в силу. Говорить о третьем законе Ньютона можно только после интегрирования по 1, 2, т. е. по длине обоих контуров. При этом, как можно показать прямым вычислением,
12 21
Сама же формула (4.5) оказывается достаточно бессмысленной. Это не мешает ей, однако, также носить имя Ампера и притом именоваться законом взаимодействия токов.

248 Магнитное поле тока [ Гл. 4
Закон Ампера во многих случаях удобно переписать в локальной форме, к которой выражение (4.4) без труда можно свести. Введем элемент поперечного сечения проводника и
представим элемент тока в виде : |
" . Далее, принимая |
во внимание, что направления и |
для тонкого проводника сов- |
падают, получаем элемент тока в следующей форме: : |
|
|
Поделив (4.4) на |
, получим плотность силы Ампера в прово- |
|
дящей среде: |
|
(4.6) |
|
||
|
" |
|
И, наконец, отнесем силу Ампера к одной заряженной частице. Для этого формулу (4.6) нужно просто разделить на концентрацию носителей тока . Вспоминая соотношение (3.5) и
ограничиваясь одним сортом носителей, получаем |
|
D , |
(4.7) |
где D — заряд частицы с учетом знака. Эта зависимость называется силой Лоренца и представляет собой самостоятельную
ценность. Можно было бы начать прямо с нее и отсюда выводить закон Ампера. Зависимость эта играет принципиально важную роль в механике заряженных частиц — как при движении в заданном внешнем поле, так и при изучении самосогласованной динамики.
Как можно видеть из (4.7), сила Лоренца относится к т. н. гироскопическим силам — при движении заряженной частицы
в заданном однородном поле работа не совершается. Из нее, в частности, следует эффект циклотронного вращения. Пусть частица с зарядом D и массой совершает нерелятивистское движение в однородном внешнем поле . Уравнение движения
D
расщепляется на два. Проекция уравнения на направление описывает равномерное движение, тогда как в плоскости, перпендикулярной , траекторией будет окружность, по которой частица будет двигаться равномерно с угловой скоростью
* < |
(4.8) |
|
|
Ее принято называть циклотронной частотой или гирочастотой.
4.2. Магнитные поля простейших токовых конфигураций. Векторные свойства магнитного поля
Самая простая задача на вычисление магнитного поля — поле в центре тонкого кольца радиуса с током :. Формула (4.3) при этом существенно упрощается; последующее интегрирование по
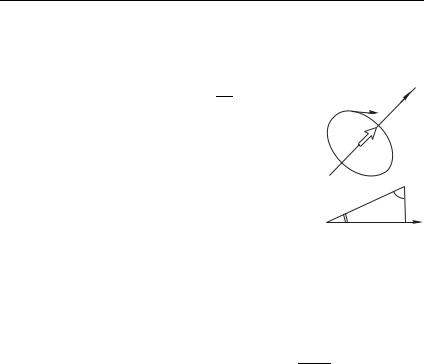
4.2 ] Магнитные поля простейших токовых конфигураций 249
сводится к умножению на длину окружности, в то же время любой элемент дает вклад в вектор , направленный по оси. Как следствие, полное поле также оказывается параллельно оси, связано с направлением тока в кольце правилом буравчика и
равно |
|
+ |
|
|
2$ |
|
|
à |
|
|
|
G |
|
|
|
+ |
|
|
|
||||
|
|
|
|
|
|
||||||
4 3 |
|
|
|
||||||||
|
|
2 |
|
|
H |
d l |
|||||
Соответственно, |
|
10: 2 . |
Несколько |
|
|
|
|||||
сложнее будет вычислить поле прямого прово- |
|
|
|
||||||||
да, но именно эта задача оказывается очень |
|
I |
|
||||||||
важной для последующих построений. |
|
|
|
||||||||
Обратимся к рис. 4.1 а. Пусть по бесконеч- |
|
|
|
||||||||
ному прямому проводу течет ток :. Из осевой |
á |
r |
R |
||||||||
симметрии задачи следует, что силовые линии |
|
|
|||||||||
|
x |
||||||||||
магнитного поля — замкнутые концентриче- |
|
||||||||||
|
|
|
|||||||||
ские окружности. (Другой |
вариант — ради- |
|
Рис. 4.1 |
|
|||||||
альные лучи — не годится, потому что усло- |
|
|
|||||||||
|
|
|
|||||||||
вие (4.1) оказалось бы нарушено.) Тот же самый ответ следует и из других соображений, а именно из геометрических свойств формулы (4.3) и из равнозначности двух полубесконечных лучей, образующих ось системы. Таким образом, G G , где —
расстояние до оси. Легко |
видеть, |
что , |
|
— см. |
|||||||||
рис. 4.1 б. Далее, |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
; |
|
|
|
# |
|
, |
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
||||
и окончательно — |
|
|
2 |
|
|
|
|
|
|
|
|||
+ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
+ |
+ |
|
|
(4.9) |
||||||
G |
|
|
|
|
|
|
|
||||||
4 |
#3 |
|
4 |
2 |
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Результат (4.9) можно чисто формально переписать и таким |
|||||||||||||
образом: |
|
:, |
|
|
|
|
|
(4.10) |
|||||
|
|
|
|
|
|
|
|
|
|||||
поскольку интегрирование по контуру в данном случае сведется к тривиальному умножению на 2$ . На этом простом примере мы познакомились с той формой закона Био и Савара, которая
чаще всего употребляется в современной физике и называется теоремой о циркуляции. Название это достаточно условно; для
вакуумного поля эквивалентность формул (4.10) и (4.3) может быть строго доказана методами векторного анализа, но в магнитоактивной среде обе эти формулы по сути постулируются в качестве определения напряженности магнитного поля. Не следует также забывать, что обе они подразумевают стационарную постановку задачи — в случае же переменных во времени полей их либо придется модифицировать, либо обеспечить их применимость какими-то сильными неравенствами.

250 |
Магнитное поле тока |
[ Гл. 4 |
При всех этих оговорках мы, тем не менее, будем придерживаться для (4.10) общепринятого названия: теорема о циркуляции. Но, имея в виду последующие ее применения, мы перепишем (4.10) в локальной (дифференциальной) форме, в которой она и фигурирует в числе основных уравнений теоретической электродинамики — уравнений Максвелла. Для этого нам придется, помимо операций дивергенции и градиента, познакомиться с новой операцией векторного дифференцирования, которая называется «ротор»:
rot ,
1 2 3
Операция может применяться к любому вектору ; мы используем вектор просто для удобства. Символическое представление операции rot в виде векторного произведения очень удобно для вывода некоторых важных соотношений. В частности, используя известные правила векторной алгебры, нетрудно получить
B , B 0,
, , , 2
—для любых функций B и . Эта же операция позволяет
придать весьма изящную форму одной из главных теорем векторного анализа — теореме Стокса.
Пусть дан некоторый произвольный контур + и векторная функция . Пусть, далее, 9 — гладкая поверхность, натянутая на наш контур, т. е. построенная так, что он является для нее линией границы. Тогда при произвольной ее форме имеет место соотношение
rot , |
(4.11) |
+
— циркуляция вектора по замкнутой границе поверхности равна потоку через эту поверхность его ротора. В этом и состоит содержание теоремы Стокса. Сравним формулы (4.11) и (4.10), представляя в последней : . Правые части обеих формул должны быть равны для произвольных + и 9. Это значит, что равны подынтегральные выражения:
rot |
(4.12) |
Это и есть теорема о циркуляции в локальной форме, входящая наряду с (2.3) и (4.1) в систему уравнений Максвелла. Она еще будет в последующих главах дополнена током смещения;
внастоящем виде этот закон является точным, по крайней мере,
вслучае токов и полей, не зависящих от времени.
