
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
7.3 ] Вращение абсолютно твердого тела вокруг неподвижной оси 131
где — толщина диска. Подставляя это выражение в (7.18), |
|||||
получаем |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
: |
|
2$3 |
2$3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Последний результат можно выразить через полную массу диска, равную произведению плотности 3 на объем диска $ 2. Окончательно получаем
: |
|
2 |
|
(7.19) |
|
|
2 |
в |
рассмотренном примере |
Нахождение момента инерции |
||||
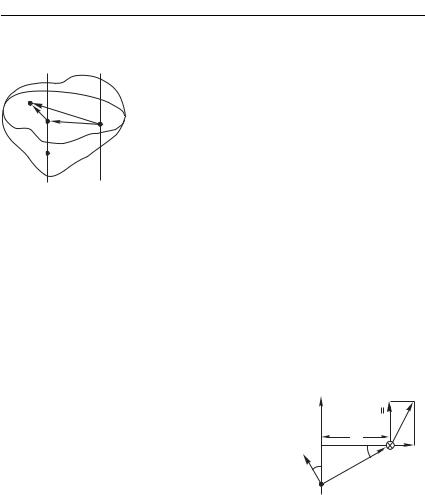
сильно упрощалось тем, что тело было однородным и симметричным, а момент инерции мы вычисляли относительно оси симметрии. Если бы мы захотели найти момент инерции диска относительно, например, оси, перпендикулярной к диску и проходящей через его край, то вычисления оказались бы более сложными. В подобных случаях нахождение момента инерции значительно облегчается, если воспользоваться следующей теоремой: «момент инерции : относительно произвольной оси равен сумме момента инерции : относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы телана квадрат расстояния между осями», т. е.
: : |
|
2 |
(7.20) |
Что касается центра масс твердого тела, то он определяется по уже известному правилу
% "% "
Для доказательства соотношения (7.20) предположим, что «старая» и «новая» оси связаны вектором параллельного переноса R
(рис. 7.9):
0 ,
где и 0 — старый и новый радиусы-векторы -й точки в плоскости ее вращения. Тогда моменты инерции связаны следующим образом:
: |
|
2 |
2 2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 :0 |
|
|
|
2 0 0 |
|
||
|
|
|
|
|
|
|
Если «старая» ось проходила через центр инерции, то 0,
а :0 : Теорема доказана. Ее обычно называют теоремой Штейнера (по имени швейцарского геометра Я. Штейнера
5*
132 |
|
Уравнение моментов. Динамика твердого тела |
[ Гл. 7 |
|||
(1796–1863)) или Гюйгенса–Штейнера. Отметим, что в ней |
||||||
отнюдь не предполагается какая-либо особая симметрия тела. |
||||||
|
|
|
В соответствии с названной теоремой, мо- |
|||
|
|
|
мент инерции диска относительно оси, |
|||
mi |
r |
|
перпендикулярной |
поверхности |
диска |
и |
|
проходящей через его край, равен найден- |
|||||
ri0 |
i |
|
||||
|
|
|||||
|
|
ному нами моменту инерции (7.19) относи- |
||||
|
R |
|||||
|
тельно оси, проходящей через центр диска, |
|||||
|
|
|
||||
C |
|
|
плюс 2 (расстояние между осями равно |
|||
|
|
|
радиусу диска ): |
|
|
|
|
|
2 |
2 3 |
|
2 |
|
Рис. 7.9 |
: |
2 |
|
|
|
|
2 |
|
|||||
Вотличие от второго закона Ньютона, в правую часть уравнения вращательного движения входит не сила, а момент силы относительно оси. При этом он играет роль, аналогичную той, которую играет сила для поступательного движения.
Вреальных задачах непосредственно сам момент силы обычно не задан, а заданы модули и направления внешних сил и точки приложения этих сил к телу, как, например, было в нашей задаче о вращении тонкого диска (см. рис. 7.8). Поэтому для
определения оси в конкретных задачах необходимо воспользоваться тем, что оси является, по определению, проекцией момента силы M относительно некоторого центра на ось вращения. Если ось вращения направлена вдоль ко-
ординатной оси , то |
|
|
z |
F |
|
|
|
|
|
||
оси |
|
|
h |
|
|
Покажем, как выражается оси через |
|
|
|
||
|
|
F |
Fh |
||
условия задачи о вращении тонкого дис- |
M |
|
|
|
|
|
r |
|
|||
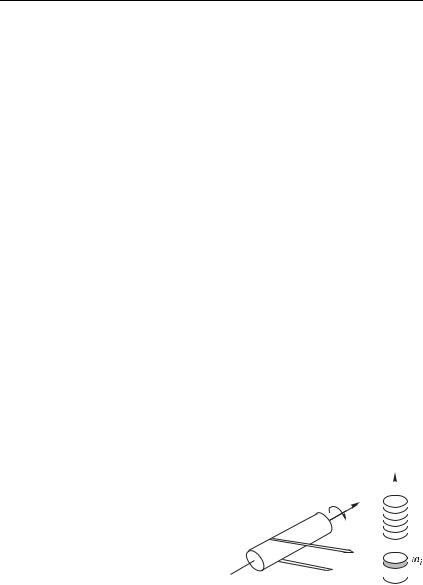
ка (рис. 7.10). Будем полагать, что центр |
|
|
|||
|
|
|
|
||
, относительно которого определен мо- |
|
|
O |
|
|
мент силы , расположен в произвольной |
|
|
Рис. 7.10 |
|
|
точке на оси вращения. Разложим вектор |
|
|
|
||
|
|
|
|
||
силы на три взаимно перпендикулярные составляющие, две |
|||||
из которых, и , параллельная и перпендикулярная оси |
|||||
вращения, лежат в плоскости, проходящей через ось вращения и |
|||||
точку приложения внешней силы, а третья — перпендикуляр- |
|||||
на к этой плоскости (эта составляющая обозначена на рисунке |
|||||
кружком с крестиком). Если в плоскости диска представить себе |
|||||
окружность радиуса с центром на оси , то составляющая |
|||||
будет направлена по касательной к этой окружности. Момент |
|||||
силы относительно центра равен сумме моментов составля- |
|||||
ющих: , где |
|
|
|
|
|
, |
, |
|
|
||
7.4 ] Следствия уравнения моментов 133
Векторное произведение направлено перпендикулярно плоскости, в которой лежат образующие его векторы. Поэтому векторы и перпендикулярны оси , и следовательно, их проекции на эту ось равны нулю. Момент имеет модуль, равный . Если составляющая на рис. 7.10 направлена «от нас», то ее момент по правилу винта направлен так, как изображено на рисунке, т. е. образует с осью угол #, косинус которого равен . Следовательно, в этом случае проекция на ось вектора положительна и имеет величину# . Если вектор направлен на рисунке «на нас», то следует направить на рисунке в противоположную сторону, и тогда проекция этого вектора на ось будет иметь величину $ # . Другие компоненты ( и ) проекций на ось , как уже отмечалось, не имеют. Следовательно, , . Таким образом, получаем для момента силы относительно оси вращения:
|
(7.21) |
|
Подчеркнем еще раз, |
что по правилу винта (см. (7.2)) знак |
|
«плюс» соответствует |
случаю, когда внешняя |
сила приводит |
к вращению вокруг направления оси против часовой стрелки, а знак «минус» соответствует вращению тела в противоположном направлении.
7.4. Следствия уравнения моментов
Рассмотрим несколько характерных задач, представляющих движение либо равновесие тела с закрепленной осью.
Первый пример — вращение однородного цилиндра вокруг неподвижной оси, совпадающей с его геометрической осью сим-
метрии , в случае, когда по |
|
|
|
|
|
|
||||
касательной к его поверхности |
|
|
z |
|
|
|||||
|
|
|
||||||||
и перпендикулярно к |
оси |
вра- |
|
z |
|
|
|
|
||
щения |
на |
цилиндр |
действует |
|
|
|
|
|
|
|
постоянная сила 0 (рис. 7.11а). |
|
|
|
|
|
|
||||
Пусть масса цилиндра , |
|
F0 |
|
|
|
|
||||
радиус — , длина — . Такая |
|
|
|
|
|
|
||||
задача является примером вра- |
O |
|
|
|
|
|
||||
щения |
вала |
какого-либо меха- |
|
|
|
|
|
O |
||
|
|
|
|
|
||||||
низма. |
В реальной |
ситуации |
à |
á |
|
|
|
|||
|
|
|
|
|||||||
между осью и валом всегда еще |
|
Рис. 7.11 |
|
|
|
|
||||
действуют |
силы трения. |
Мы |
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
будем полагать, что они достаточно малы, чтобы ими можно было пренебречь. Тогда единственный момент силы, не равный нулю, есть
оси 0
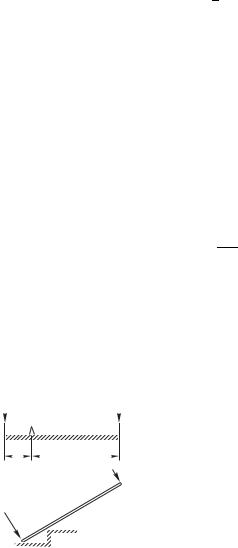
134 |
Уравнение моментов. Динамика твердого тела |
[ Гл. 7 |
Момент инерции цилиндра относительно оси симметрии легко найти, если мысленно представить цилиндр как совокупность тонких дисков с массами , «нанизанных» на ось (рис. 7.11 б), откуда сразу следует, что искомая величина дается все той же формулой (7.19):
: 12 2
Разумеется, теперь в ответ входит полная масса цилиндра . Таким образом, уравнение моментов (7.16) приобретает вид
2 |
|
2 0 |
|
(7.22) |
|
2 |
|
||||
|
|
||||
Чтобы решение было однозначно определено, необходимо, как мы уже знаем, задать начальные условия: начальные значения угла поворота и угловой скорости . Выберем, например, начальные условия в виде: 0 0, 0 0.
Уравнение (7.22) с математической точки зрения полностью аналогично уравнению, определяющему движение тела, падающего под действием силы тяжести, и его решение также находится без труда на основе элементарных правил вычисления производных от простейших функций. Удовлетворяющее начальным условиям решение уравнения (7.22) имеет вид
0 2
Мы уже отмечали, что одной из особенностей вращательного движения тела вокруг неподвижной оси, отличающей его от поступательного движения, является зависимость вращения не непосредственно от величины приложенной к телу силы, а от момента этой силы относительно оси вращения. Так, в рассмотренном выше примере движение диска определяется не величи-
ной силы 0, а ее моментом относительно оси вращения, то есть |
||||||||||
произведением силы на плечо (в нашем случае — 0 ). И даже |
||||||||||
|
|
|
|
|
|
|
|
|
|
при очень малом значении модуля силы это |
|
F1 |
|
|
|
F2 |
|
произведение может иметь большую вели- |
|||
|
|
|
|
O |
|
|
|
чину, если плечо силы достаточно велико. |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Эта особенность вращательного движе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h1 |
|
|
h2 |
ния вокруг неподвижной оси лежит в осно- |
|||
|
|
|
|
|
|
|
|
|
|
ве работы рычага — одного из древнейших |
|
|
|
|
|
à |
|
|
|
||
|
|
|
|
|
|
|
|
орудий труда человека. Схематически лю- |
||
|
|
|
|
|
|
|
F2 |
|||
|
|
|
|
|
|
|
|
|
|
бой рычаг можно представить, как тонкий |
|
|
|
|
|
|
|
|
|
|
стержень, который может вращаться во- |
|
|
F1 |
|
|
|
|
|
|
круг неподвижной оси, перпендикулярной |
|
|
|
|
|
|
|
|
|
|
|
стержню и проходящей не через его центр. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
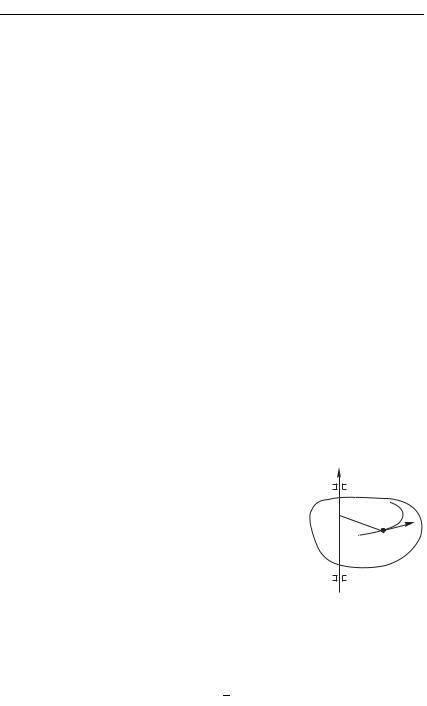
На рис. 7.12 а изображен такой стержень, |
|
|
|
|
|
á |
|
|
|
||
|
|
|
|
|
|
|
|
который может вращаться вокруг горизон- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.12 |
тальной оси, перпендикулярной стержню |
||||
7.4 ] |
Следствия уравнения моментов |
135 |
|||||
(в нашем случае — перпендикулярно плоскости рисунка). Точка |
|||||||
стержня, через которую проходит ось вращения, делит стер- |
|||||||
жень на неравные отрезки длиной 1 и 2. Допустим стержень |
|||||||
расположен горизонтально, и к концам стержня, перпендикуляр- |
|||||||
но ему и оси вращения, приложены две силы — 1 и 2. Будем |
|||||||
считать стержень достаточно легким, так что действием силы |
|||||||
тяжести по сравнению с силами 1 и 2 можно пренебречь. |
|||||||
Из уравнения моментов (7.5) можно найти условие равно- |
|||||||
весия стержня, то есть условие, при котором стержень будет |
|||||||
оставаться неподвижным или вращаться с постоянной угловой |
|||||||
скоростью. В нашем случае уравнение моментов имеет вид |
|||||||
|
:0 |
2 2 1 1, |
(7.23) |
||||
|
|
|
|
|
|
||
где :0 — момент инерции стержня относительно оси враще- |
|||||||
ния. Моменты сил 1 и 2 относительно оси вращения входят |
|||||||
в уравнение с разными знаками в соответствии с «правилом |
|||||||
винта»: в одном случае сила стремится повернуть стержень по |
|||||||
часовой стрелке, а в другом — против. Приравнивая левую часть |
|||||||
уравнения (7.23) нулю, получаем условие равновесия в виде |
|||||||
|
|
1 1 2 2 |
|
|
|||
Из него следует, что как бы ни была велика, например, сила |
|||||||
1, ее всегда можно уравновесить малой силой 2, если выбрать |
|||||||
плечо 2 достаточно большим по сравнению с 1. |
|||||||
Приспособления, использующие рассмотренное выше свой- |
|||||||
ство вращательного движения вокруг неподвижной оси, полу- |
|||||||
чили название рычагов. В качестве примера рис. 7.12 б иллю- |
|||||||
стрирует, как свойство рычага используется при работе лопаты. |
|||||||
«Правило рычага» было известно уже в глубокой древности, и |
|||||||
впервые оно было, по-видимому, четко |
|
||||||
сформулировано в третьем веке до нашей |
z |
||||||
эры знаменитым древнегреческим ученым и |
|
||||||
изобретателем Архимедом. |
|
|
|
ri |
|||
Выведем теперь выражение для кинети- |
|||||||
ческой энергии тела, вращающегося вокруг |
vi |
||||||
неподвижной оси, которое может оказаться |
mi |
||||||
полезным при изучении некоторых особен- |
|
||||||
ностей вращательного движения на основе |
|
||||||
законов сохранения. Пусть тело вращается |
O |
||||||
вокруг оси (рис. 7.13). Разобьем мыслен- |
Рис. 7.13 |
||||||
но тело на элементарные массы . Линей- |
|||||||
|
|||||||
ная скорость элементарной массы равна , где — |
|||||||
расстояние массы от оси . Следовательно, для кинетиче- |
|||||||
ской энергии |
-й элементарной массы получается выражение |
||||||
|
|
2 |
1 |
2 2 |
|
||
|
|
2 |
2 |
|
|
||

136 Уравнение моментов. Динамика твердого тела [ Гл. 7
Кинетическая энергия тела слагается из кинетических энергий
его частей: |
|
1 |
|
2 2 |
|
|
|
|
|||
|
|
||||
2 |
Сумма в правой части этого соотношения представляет собой момент инерции тела : относительно оси вращения. Таким образом, кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна
|
1 |
: |
|
2 2 |
|
(7.24) |
|
|
2 |
|
|
2+ |
|
|
|
Сравнивая соотношения (7.17) и (7.24), соответственно, со вторым законом Ньютона и выражением для кинетической энергии материальной точки, можно убедиться в существовании между ними глубокой аналогии. Поэтому в случае, когда дви-
жение тела есть изменение во времени не линейных, но угловых (ориентационных) координат, говорят, что L есть обобщенный импульс, M — обобщенная сила, а : — обобщенная масса, соответствующие обобщенной координате . (Эта терминоло-
гия построена отнюдь не ради данного частного случая — на таком языке формулируется механика в самом общем виде, который называется аналитической механикой.)
7.5. Трехмерное движение твердого тела. Гироскопы
Замечание, сделанное в конце предыдущего параграфа, побуждает нас представить уравнения (7.17) и (7.24) в векторной
форме, для чего целесообразно включить в рассмотрение понятие вектора угловой скорости и следующие из этого понятия
формулы (2.13):
|
; |
|
|
(7.25) |
||||
|
|
|
|
|
|
|
|
|
С учетом (7.25) формула (7.12) должна быть переписана в |
||||||||
виде |
|
|
2 , |
|
||||
|
|
|
|
|||||
а (7.15) — соответственно, |
|
|
|
|
|
|||
|
|
|
|
: , |
(7.26) |
|||
наконец, |
уравнение |
моментов |
(7.17) принимает |
следую- |
||||
щую форму: |
|
|
|
|
|
|
(7.27) |
|
|
|
: |
|
|
|
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Сколь |
ни велик |
соблазн |
|
|
|
|||
отнести уравнения (7.26), (7.27) |
||||||||
к произвольному неодномерному движению, делать это надлежит с большой осторожностью, поскольку выводились они для частного случая тела с закрепленной осью, когда вектор удерживается неизменным по направлению, а достигается это в общем случае несимметричного вращающегося тела посредством
7.5 ] |
Трехмерное движение твердого тела. Гироскопы |
137 |
момента реакции в опорах оси, дополнительного к правой части (7.17), учитывающей только вращающие моменты.
В общем случае трехмерного движения твердого тела произвольной формы (точнее — произвольной геометрии массы) ревизии подвергается прежде всего формула (7.26). Векторы и L оказываются, вообще говоря, не параллельны. Соответственно, уравнение моментов (7.15) лишь в случае осевой симметрии сводится к (7.27).
Оказывается, однако, что в каждом твердом теле имеются три взаимно перпендикулярные, проходящие через центр масс, оси, такие, что при вращении твердого тела вокруг них зависимость возникающего момента импульса от угловой скорости
вращения имеет простой вид: : , где : — момент инерции тела относительно оси вращения. Эти оси называются главными осями инерции твердого тела. Мы не будем останавливаться
на доказательстве этого утверждения, а рассмотрим основные следствия из него.
Представим себе, что мы сообщили телу вращение с угловой скоростью вокруг одной из его главных осей. Возникающий
утела момент импульса L равен, согласно вышесказанному,
: . Если при этом на тело не действуют внешние силы или суммарный момент внешних сил равен нулю, то, согласно (7.27),
: , и, следовательно, . Другими словами,
в случае, когда момент действующих на тело внешних сил равен нулю, угловая скорость вращения тела вокруг любой из его главных осей инерции сохраняется по величине и направлению.
Определение фактического положения главных осей в твердом теле облегчается правилом, которое гласит: все оси симметрии твердого тела являются его главными осями инерции. (В частном случае тела вращения происходит, как принято говорить, вырождение: любая ось, перпендикулярная оси симметрии, является главной осью, так что в этом случае их будет не три, а бесконечно много.) Поэтому поведение твердых тел, вращающихся вокруг своих осей симметрии, обладает рядом специфических особенностей, широко используемых в технике. Массивные симметричные тела, быстро вращающиеся вокруг оси
симметрии, которая, в свою очередь, свободно ориентируется в пространстве, получили название гироскопов. Способность оси
гироскопа сохранять при определенных условиях свое направление в пространстве лежит в основе их использования в качестве навигационных приборов. Само же это свойство обусловлено сохранением момента импульса вкупе с тем обстоятельством, что угловая координата, характеризующая вращение, меняется быстрее, нежели любая другая:
, |
(7.28) |

138 Уравнение моментов. Динамика твердого тела [ Гл. 7
где — угловая скорость поворота оси волчка в пространстве. Именно в этом смысле вращение гироскопа должно быть быстрым.
Рассмотрим гироскоп, имеющий вид массивного колеса, подвешенного несимметричным образом, как показано на рис. 7.14.
|
|
|
|
(Для демонстрации удобно исполь- |
|
|
|
|
зовать велосипедное колесо, раскру- |
|
|
|
|
|
|
T |
|
|
ченное электромоторчиком). |
O |
|
|
M |
Угловая скорость и момент им- |
|
|
|
пульса L направлены по оси. На ги- |
|
|
|
|
|
|
|
h |
C |
|
роскоп действует сила тяжести и на- |
|
|
тяжение нити T. Вычисляя момент |
||
|
|
|
; L |
|
|
|
|
сил относительно центра инерции |
|
|
|
|
|
|
|
|
Рис. 7.14 |
|
гироскопа, мы должны учесть вклад |
|
|
|
в него лишь от силы натяжения, так |
как момент силы тяжести относительно точки % равен нулю. Момент силы натяжения равен и направлен так, как показано на рис. 7.14. Из уравнения моментов (7.5) следует, что приращение вектора L будет происходить в направлении момента, то есть ось вращения должна поворачиваться в горизонтальной плоскости — на рис. 7.14 это показано двойной стрелкой.
Ответ лишь на первый взгляд кажется парадоксальным. В наших рассуждениях мы молчаливо считали выполненным условие (7.28), в котором под следует понимать именно скорость поворота вектора L. Таким образом, для демонстрации нетривиального поведения гироскопа он должен быть как следует раскручен. В этом случае он не может опрокинуться, хотя и подвешен несимметричным образом. В самом деле, при опрокидывании вектор L должен был бы повернуться в вертикальной плоскости. Но момент внешней силы для такого поворота должен быть направлен по вертикали, а значит, сама сила должна быть горизонтальна и направлена по нормали к оси. Но при подвешивании гироскопа на нити такая сила отсутствует. Вот если бы посредством жесткой муфты гироскоп был лишен степени свободы, позволяющей его оси поворачиваться в горизонтальной плоскости, то реакция опоры была бы ориентирована именно так, и колесо бы опрокинулось.
Мы не случайно упомянули именно велосипедное колесо. Б´ольшая устойчивость быстро движущегося велосипеда в сравнении с неподвижно стоящим, не в последнюю очередь обусловлена именно гироскопическим эффектом вращающихся колес.
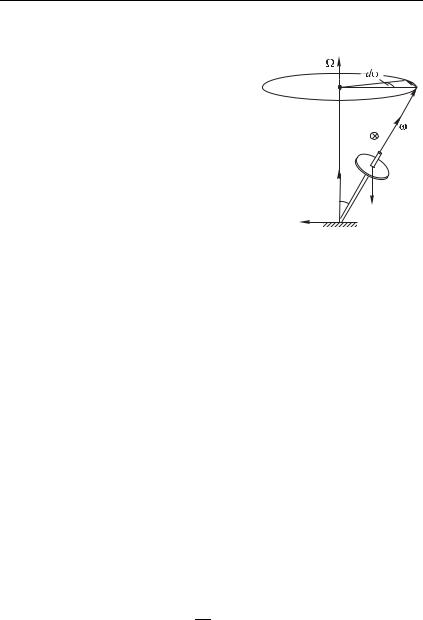
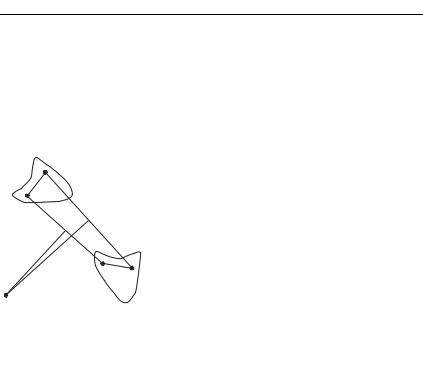
Рассмотрим задачу о так называемой регулярной прецессии волчка (рис. 7.15). Как известно, быстро вращающийся волчок, будучи слегка выведен из вертикального положения, не падает, но приобретает дополнительное вращение в наклонном положении, угловая скорость которого удовлетворяет неравенству (7.28). Когда же указанное неравенство, по мере замедления
7.5 ] |
Трехмерное движение твердого тела. Гироскопы |
139 |
||
вращения волчка, еще даже не нарушается, но перестает быть |
||||
сильным (& вместо ), на вращение накладываются сложные |
||||
нерегулярные движения (их называ- |
|
|
||
ют |
нутациями). Эту стадию дина- |
|
dL |
|
мики волчка мы рассматривать не |
|
|||
|
|
|||
будем ввиду математической слож- |
|
|
||
ности, однако объяснить регулярную |
|
L |
||
прецессию для нас труда не составит. |
M |
|
||
|
Обратимся к рис. 7.15. Пусть % — |
|
||
|
|
|
||
центр инерции волчка, — точка |
C |
|
||
опоры, причем % Поскольку |
|
|||
N |
|
|||
в точке , помимо реакции опоры N, |
|
|||
|
mg |
|||
приложена еще и сила трения тр, |
||||
|
|
|||
нам, вообще говоря, не известная, |
Fòð O |
|
||
момент сил проще вычислять относи- |
|
|
||
тельно точки . Он, очевидно, равен |
Рис. 7.15 |
|
||
и направлен от нас пер- |
|
|
||
пендикулярно плоскости рисунка. При условии (7.28) мы вправе |
||||
связать момент импульса гироскопа L исключительно с угловой |
||||
скоростью и считать его направленным строго по оси. |
|
|||
|
Из уравнения моментов (7.15) следует, что за малое время |
|||
момент импульса L получает приращение |
|
|
||
,
причем, как и сам вектор M, это малое приращение перпендикулярно L.
Таким образом, эволюция вектора L свелась к повороту, который в горизонтальной плоскости можно характеризовать углом
|
|
$ |
|
|
$ |
$ |
|
Получается, что ось волчка и в самом деле должна прецессировать, причем угловая скорость прецессии не зависит от угла :
, |
(7.29) |
+0 |
|
где :0 — момент инерции волчка относительно оси симметрии. Условие (7.28) можно в данном случае представить в эквивалентном виде :0 2 Уравнение моментов можно переписать в векторной форме
,
арезультат (7.29), соответственно, примет вид
|
(7.30) |
+0
140 |
|
Уравнение моментов. Динамика твердого тела |
[ Гл. 7 |
||||
|
7.6. Плоское движение твердого тела |
|
|
||||
По самому определению, плоское движение отвечает изме- |
|||||||
нению во времени лишь трех координат твердого тела, на- |
|||||||
пример, двух декартовых , и одной ориентационной . |
|||||||
Последняя может и выпадать, если движение — чисто по- |
|||||||
ступательное. К плоскому сведется и существенно трехмер- |
|||||||
ное движение, если оно является поступательным по одной из |
|||||||
|
|
|
|
декартовых координат. |
|
|
|
|
B |
|
|
При плоском движении, как легко |
|||
|
|
|
усмотреть из рис. 7.16, любое переме- |
||||
|
|
|
|
||||
A |
|
|
|
щение можно представить как поворот |
|||
|
|
|
|
вокруг некоторой точки (точнее — |
|||
|
|
|
|
оси, проходящей через и ортогональ- |
|||
|
|
|
|
ной плоскости перемещения). Особый |
|||
|
|
|
|
случай — поступательное движение, при |
|||
|
|
A |
B |
котором точка как бы перемещается |
|||
|
|
|
в бесконечность. |
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
Как следствие, малое перемеще- |
|||
|
Рис. 7.16 |
|
ние представляется как поворот вокруг |
||||
|
|
некоторой оси на малый |
угол |
. |
|||
|
|
|
|
||||
Если |
этот |
поворот |
происходит за время |
, то |
величина |
||
|
называется мгновенным значением угловой ско- |
||||||
рости, а сама ось, проходящая через точку — мгновенной |
|||||||
осью |
вращения. Если, например, мы можем |
установить, |
что |
||||
вданный момент времени какая-то точка тела имеет нулевую скорость, то именно через нее проходит мгновенная ось вращения; если же мы наблюдаем две таких точки, то 0 для всего нашего тела.
Из рис. 7.16 можно понять также и то, что плоское перемещение можно представить не только в виде поворота, но и
ввиде комбинации любого поступательного перемещения и поворота. Просто, перенеся тело, которому принадлежит отрезок ,
влюбую заданную точку, мы проведем затем построение, эквивалентное тому, которое показано на рис. 7.16. Если мы вновь обратимся к малым перемещениям, то сдвинув любую точку
тела на некоторый вектор , , мы затем осуществим поворот на угол . Соответственно, деля на , получаем представление движения скоростью и угловой скоростью . Физический смысл — скорость системы отсчета, в которой рассматривается вращение.
Обратимся еще раз к рис. 7.16. Какова бы ни была упомянутая комбинация поступательного и вращательного перемещений, угол между отрезками и остается инвариантом. Иными словами, как бы мы ни сместили мгновенную ось, тело придется повернуть на один и тот же угол. Еще раз возвращаясь к малым
