
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf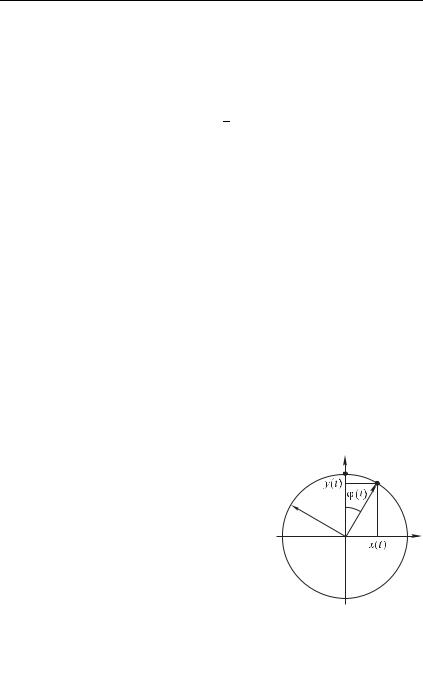
2.2 ] Равномерное движение по окружности 31
(2.5) мы получим
0 0 0 ,
где мы учли, что сумма элементарных промежутков времени равна времени , за которое тело прошло путь . Таким образом, для равномерного движения мы получаем
0 ,
то есть модуль скорости равномерного движения равен пути, проходимому телом за единицу времени. Именно таково пони-
мание скорости в обыденной жизни.
Аналогичным образом определяется при неодномерном движении и вектор ускорения материальной точки:
|
|
(2.7) |
|
0 |
|
Итак, ускорение — это производная скорости по времени. Так же, как и радиус-вектор и скорость , ускорение
является векторной величиной. Модуль и направление можно всегда вычислить, если известен закон движения тела по траектории, то есть известна зависимость радиуса-вектора от времени.
2.2.Равномерное движение по окружности
Вкачестве примера таких вычислений рассмотрим, как определяется модуль и направление ускорения при равномерном движении материальной точки по окружности радиуса со скоростью, модуль которой равен . С таким типом движения приходится сталкиваться очень часто: от
вращения на карусели до движения |
|
y |
A |
|
|
|
|
спутников и космических кораблей. |
|
|
|
|
|
B |
|
Важным шагом при решении лю- |
|
|
|
|
|
|
|
бой механической задачи является вы- |
|
R |
|
|
t |
) |
|
бор системы отсчета. В нашем случае |
|
r |
( |
|
|||
|
|
|
|||||
|
|
|
|
x |
|||
|
|
|
|
|
|||
мы поместим начало декартовой си- |
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
стемы координат в центр окружности, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по которой движется тело, а оси |
|
|
|
|
|
|
|
и расположим в плоскости движения |
|
|
|
|
|
|
|
(рис. 2.2). Пусть в начальный момент |
|
|
|
|
|
|
|
времени тело находилось в наивысшей |
|
|
|
|
|
|
|
точке окружности , то есть началь- |
|
Рис. 2.2 |
|
|
|||
ные значения проекций радиуса-векто- |
|
|
|
|
|
|
|
ра равны 0 0, 0 . Проекция всегда равна ну- |
|||||||
лю, так как движение происходит в плоскости . Обозначим |
|||||||
меняющийся со временем угол между |
и |
через |
. |
||||

32 Введение в кинематику [ Гл. 2
Тогда траектория движения будет описываться зависимостью от времени проекций радиуса-вектора , а именно:
,
(2.8)
Отношение пройденной телом дуги окружности к радиусу определяет угол , измеренный в радианах. При равномерном движении тела по окружности длина дуги равна пройденному пути , и поэтому
|
|
|
|
, |
(2.9) |
|
|
||||
|
|
|
|
||
где — угловая скорость движения тела по окружности. Определим сначала проекции скорости и . Используя правила для вычисления производных от тригонометрических
функций, получаем с помощью (2.8), (2.9):
|
|
, |
|
|
|||
|
|
|
|
Как следствие, получаем известную формулу, связывающую линейную и угловую скорости при равномерном движении по
окружности: |
|
|
|
|
|
2 2 |
|
|
|
|
|
Теперь можно получить и значения проекций ускорения на оси декартовых координат:
|
|
2 , |
2 |
|
|
|
Отсюда находим окончательное выражение для модуля вектора :
|
|
2 2 |
|
|
2 2 |
|
(2.10) |
||
|
|
|
|
|
|
|
|
|
|
Нетрудно усмотреть, что |
и меняются |
со временем |
||
синхронно с проекциями радиуса-вектора и по законам
и , то есть векторы и связаны соотношением
2 |
(2.11) |
Знак «минус» означает, что вектор направлен противоположно вектору , т. е. ускорение материальной точки при ее равномерном движении по окружности направлено к центру.
По этой причине ускорение, модуль которого определяется фор-
мулой (2.10), а направление совпадает с нормалью к траектории, называют обычно центростремительным ускорением.
Если же сама скорость неодномерного движения меняется по величине, этому соответствует ненулевая компонента ускорения по направлению касательной. А вот по направлению так
2.2 ] |
Равномерное движение по окружности |
33 |
||
называемой бинормали — вектора, ортогонального плоскости, |
||||
содержащей векторы нормали и касательной, проекции как ско- |
||||
рости, так и ускорения всегда равны нулю. Понятие угловой |
||||
скорости можно обобщить и на этот случай, подобно тому, как |
||||
это делается при рассмотрении прямолинейного неравномерного |
||||
движения для линейной скорости. Определим угловую скорость |
||||
при неравномерном движении по окружности как производную |
||||
по времени естественной — угловой — координаты: |
|
|||
|
|
|
(2.12) |
|
|
|
|
|
|
Более сложные траектории, а также основные законы неравно- |
||||
мерного движения по криволинейной траектории будут рассмот- |
||||
рены в последующих главах нашего курса. |
|
|||
В механике, как и в любом последующем разделе физики, |
||||
особую ценность количественным результатам придает их инва- |
||||
риантность по отношению к выбору системы координат. В част- |
||||
ности, векторная алгебра, а в дальнейшем и векторный анализ, |
||||
тем и привлекательны в качестве языка, на котором формулиру- |
||||
ются законы физики. Формулы (2.11), (2.12) представляют собой |
||||
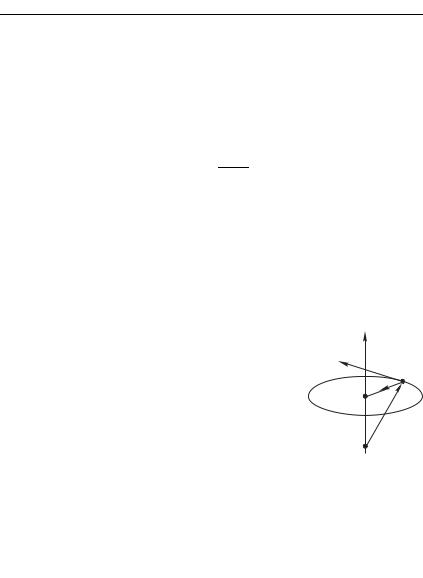
первый шаг в данном направлении, но и |
|
|||
они оставляют без должной определенно- |
|
|||
сти вопрос о плоскости, в которой происхо- |
v |
|||
дит движение тела по окружности. Иными |
||||
|
||||
словами, мы полностью определим движе- |
a |
|||
ние тела в пространстве, если дополним на- |
r |
|||
ше рассмотрение уравнением плоскости (см. |
||||
|
||||
рис. 2.2). |
|
|
||
Эту |
проблему мы можем с |
успехом |
|
|
разрешить, введя вектор угловой скорости |
|
|||
(рис. 2.3). Определяем вектор как перпен- |
Рис. 2.3 |
|||
дикулярный плоскости нашей окружности и |
|
|||
направленный так, чтобы при наблюдении со стороны его конца |
||||
движение точки по окружности происходило против часовой |
||||
стрелки. Иначе говоря, вектор как бы «ввинчивается» в про- |
||||
странство по закону правого винта. Тогда скорость и ускорение |
||||
при равномерном движении по окружности могут быть представ- |
||||
лены в виде векторных произведений: |
|
|||
; |
|
(2.13) |
|
|
|
Напомним, что по определению векторного произведения вектор
ортогонален плоскости (a b), образует с этими векторами правую тройку: , , , , и равен по модулю
,
Остановимся кратко на инвариантности формул (2.13), то есть на независимости этих соотношений от выбора системы
2 Основы физики. Т. I

34 Введение в кинематику [ Гл. 2
координат. Первое из этих соотношений позволяет выбирать начало координат в любой точке оси вращения, в данном случае — прямой, нормальной к плоскости нашей окружности и проходящей через ее центр. Эта инвариантность прямо следует из свойства векторного произведения: если , то 0. Второе из равенств (2.13) справедливо всегда, если центр окружности неподвижен. Заметим, что кинематически оно эквивалентно первому. Действительно, оба вектора, и , при указанных выше условиях равномерно вращаются, не изменяя модуля, с одной и той же угловой скоростью . Таким образом, можно сформулировать и более общее утверждение. Если некоторая векторная величина b изменяется во времени так, что это изменение можно представить как вращение с угловой скоростью , то имеет место
соотношение |
|
|
(2.14) |
|
|
||
|
|
||
|
|
|
Далее, в гл. 7 будет рассмотрено вращательное движение
твердого тела, и тогда первое из соотношений (2.13) можно будет трактовать уже как векторное поле скоростей, т. е. заданную
векторную функцию в пространстве (и может быть, во времени). Скорость v привязывается в этом случае не к материальной точке как элементу твердого тела, а к точке пространства, и с этой скоростью движется элемент тела в тот момент, когда он «посещает» данную точку пространства. (В дальнейшем такое представление переносится на течение жидкости.)
Следует, отметить, что — не совсем обычный вектор. При поворотах системы координат он, подобно истинным векторам, например, и , сохраняет величину и направление. Но если подвергнуть систему координат операции отражения, , , , , то мы должны поменять знак . Это следует формально из того, что формулы (2.13) должны определятьи инвариантным образом. Возможна и простая физическая (или геометрическая) интерпретация этого свойства: мы определили через правило винта, но при перемене знака всех трех
координат правый винт трансформируется в левый и наоборот. Такие величины называются псевдовекторами. Псевдовек-
тором оказывается векторное произведение любых двух истин-
ных векторов. (Соответственно, смешанное произведение a[b c] называется псевдоскаляром.) Таким образом, мы видим, что
объявлять векторной любую величину, имеющую направление и представимую в трех проекциях, было бы неразумно. Повышенные требования к объекту, претендующему на звание вектора, придают истинно векторным законам дополнительную доказательную силу.
Но пока и поскольку мы не оперируем отражением системы координат, может рассматриваться именно как вектор, из чего
2.3 ] |
Приближение абсолютно твердого тела |
35 |
проистекают вполне практические следствия. При решении задач на динамику твердого тела конечных размеров часто бывает удобно представлять движение тела как сумму двух или более вращений,
либо производить обратную операцию. Что же касается переноса начала координат либо перехода в систему отсчета, движущуюся относительно данной с некоторой скоростью, то к этим операциям в контексте формул (2.13) мы еще вернемся в последующих главах.
2.3. Приближение абсолютно твердого тела и приближение материальной точки
Не только история науки, но и повседневный человеческий опыт показывают, что приступая к изучению какого-либо нового явления, разумно не пытаться сразу же искать объяснения всех его зачастую очень сложных сторон и деталей, а двигаться шаг за шагом от понимания простых закономерностей к пониманию все более полной картины. Так и нам при изучении механики следует начать с рассмотрения простейших типов движения, на примере которых мы освоим основные идеи и понятия этой науки, после чего круг изучаемых движений можно будет расширить. В самом деле, трудно рассчитывать на то, что мы с первых же шагов сможем, например, разобраться в законах птичьего полета. Только лишь для строгого определения положения птицы относительно выбранной системы координат в некоторый момент времени необходимо знать радиусы-векторы различных точек
крыльев, корпуса, хвостового опе- |
|
|
|
||
рения, головы |
(рис. 2.4), |
так что |
|
|
A |
математическое |
описание |
полета |
|
|
|
|
|
|
|||
неизбежно будет содержать соот- |
|
) |
|
||
|
t |
|
|||
z |
( |
|
|||
ношения между большим числом |
rA |
|
|||
|
|
B |
|||
зависящих от |
времени величин. |
|
|
||
|
) |
|
|||
|
t |
|
|||
|
( |
|
|||
Получить из этих соотношений тра- |
|
rB |
C |
||
|
|
||||
екторию полета наверняка окажет- |
|
(t) |
|
||
ся необычайно сложной задачей. |
|
r |
|
||
|
C |
|
|||
|
|
|
|||
Сформулируем теперь |
наше |
|
|
y |
|
первое важное упрощение. Оно со- |
x |
|
|
||
стоит в том, что мы будем на |
|
|
|||
|
Рис. 2.4 |
|
|||
первых этапах |
изучать движение |
|
|
||
только абсолютно твердых тел. Этим термином принято обозначать тела, при движении которых можно пренебречь их деформациями, то есть смещениями одних частей тела относительно других. Под влиянием внешних воздействий все
тела испытывают те или иные деформации. Стальной стержень
2*
36 Введение в кинематику [ Гл. 2
даже при обычных изменениях атмосферного давления и температуры меняет свои размеры и форму, хотя эти изменения можно заметить только с помощью весьма чувствительных приборов. Но если этот стержень является деталью достаточно грубого механизма, то такими деформациями можно пренебречь и его движение можно будет рассчитывать при конструировании механизма по законам движения абсолютно твердого тела, о которых пойдет речь в дальнейшем. Однако если тот же стержень является деталью сложного электронного прибора, то учет его деформаций может оказаться главной задачей конструктора, и тогда приближение абсолютно твердого тела будет неприменимо. Поэтому представление об абсолютно твердом теле как о теле, не подверженном вообще никаким деформациям, является всего лишь определенным приближением к реальной действительности, удобной идеализацией (или, как говорят физики, моделью), применимость или неприменимость которой при рассмотрении движения тела зависит от конкретных условий.
Относительная простота законов движения абсолютно твердого тела обусловлена уже тем, что для строгого математического описания его положения в какой-либо системе координат требуется задавать гораздо меньше пара-
|
|
|
|
|
B |
метров (координат), чем для деформируе- |
||||
z |
|
|
|
|
|
|
|
мого тела. Число независимых параметров, |
||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
однозначно определяющих положение тела |
||
|
|
|
|
A |
|
|
|
в пространстве, называют числом степе- |
||
|
|
|
|
rA(xA, yA, zA) |
ней свободы. Посмотрим, чему равно число |
|||||
|
|
|
|
степеней свободы абсолютно твердого тела. |
||||||
|
|
|
|
|
|
|
|
|||
O |
y |
Представим для большей наглядности, что |
||||||||
x |
à |
|
|
наше тело имеет форму параллелепипеда, |
||||||
|
|
|
|
|
|
|
как изображено на рис. 2.5, и |
пусть ли- |
||
z |
|
|
|
|
|
|||||
|
|
|
|
|
ния является пересечением каких-либо |
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
B |
двух его |
граней. Полное число |
степеней |
||
|
|
свободы такого тела можно определить, на- |
||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
пример, как сумму двух слагаемых: одно — |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
это число степеней свободы точки и дру- |
||
|
|
|
|
O |
|
|
|
гое — это число независимых параметров, |
||
|
|
|
|
|
|
|
которые однозначно определяют положение |
|||
|
|
A |
|
y |
||||||
x |
á |
|
|
тела при уже фиксированном в |
простран- |
|||||
|
|
стве положении точки . Число степеней |
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
Рис. 2.5 |
свободы точки равно трем — это, напри- |
|||||
|
|
|
|
мер, три декартовы координаты , , , |
||||||
|
|
|
|
|
|
|
|
|||
определяющие радиус-вектор |
точки в заранее выбранной |
|||||||||
системе координат (рис. 2.5 а). При фиксированном положении одной точки положение всего тела еще может быть различным, и это положение можно окончательно зафиксировать, если задать три угла поворота , и (рис. 2.5 б). Угол — это угол

2.3 ] Приближение абсолютно твердого тела 37
наклона линии к оси исходной системы координат. Угол— это угол поворота линии вокруг оси при фиксиро-
ванном угле наклона . И, наконец, угол — это угол поворота всего тела вокруг линии . Итак, число степеней свободы абсолютно твердого тела равно шести: три координаты точ-
ки — , , , и три угла поворота — , , .
Таким образом, для описания произвольного движения абсолютно твердого тела необходимо знать, как меняются со временем всего шесть параметров, т. е. необходимо знание шести функций от времени: , , , , , . Хотя мы пока еще не знаем законов движения твердого тела, т. е. соотношений или уравнений, позволяющих определить эти функции и, тем самым, предсказать траекторию движения тела, можно заранее предположить, что эти законы будут в общем случае очень сложными — даже из школьной математики мы знаем, что чем больше число неизвестных, тем сложнее решение задачи. Поэто-
му рассмотрим сначала движения, описа- |
B |
|
ние которых не требует столь большого |
||
|
||
количества зависящих от времени величин. |
B |
|
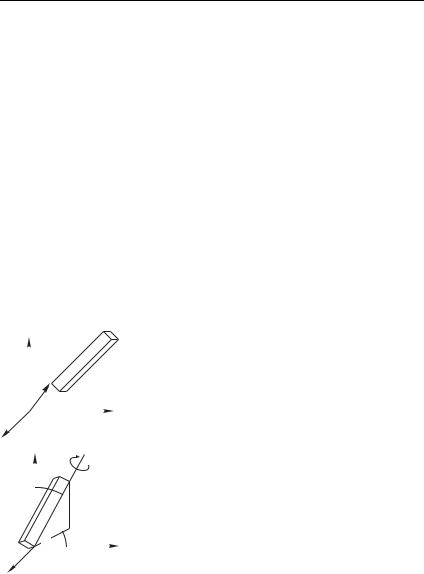
Заметим для этого, что любое движе- |
|
|
ние абсолютно твердого тела можно разло- |
A |
|
жить на два основных вида движения — |
||
B |
||
поступательное и вращательное. Посту- |
A |
|
пательное движение — это такое движе- |
|
|
ние, при котором любая прямая, связанная |
|
|
с движущимся телом, остается параллель- |
A |
|
ной самой себе (рис. 2.6). При вращатель- |
Рис. 2.6 |
|
ном движении все точки тела движутся по |
|
окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения (рис. 2.7). При этом происходит
изменение ориентации тела. Отметим, что при конечных переме-
|
|
щениях поворота тела относительно |
|
|
|
только одной оси, вообще говоря, |
|
|
|
недостаточно, чтобы |
перевести его |
|
|
в новое положение. Сама ось вра- |
|
|
|
щения может находиться вне тела. |
|
|
|
Например, перемещение тела из по- |
|
|
|
ложения a в положение в на рис. 2.8 |
|
|
|
можно представить |
как поступа- |
à |
á |
тельное движение из положения a в |
|
|
|
положение б и последующего пово- |
|
Рис. 2.7 |
рота тела на 180Æ вокруг оси . |
|
Главным для нас является сейчас тот факт, что если абсолютно твердое тело совершает только поступательное движение, то все его положения в пространстве однозначно определяются положением всего одной какой-либо его точки, например, точ-
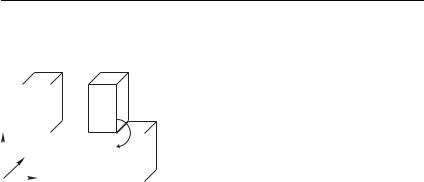
38 Введение в кинематику [ Гл. 2
ки на рис. 2.8. Следовательно, при математическом описании поступательного движения твердого тела его размеры не играют роли, и все это тело можно заменить
à |
|
á |
|
точкой, положение которой в про- |
|||
|
|
|
|
|
|
странстве определяется в общем слу- |
|
|
|
C |
|
C |
чае всего тремя степенями свободы — |
||
|
|
|
B |
|
B |
например, |
декартовыми координата- |
|
|
A |
|
A |
ми , |
, , определяющими |
|
z |
|
|
|
|
|
радиус-вектор этой точки. Это и есть |
|
|
|
|
|
|
|
||
y |
|
|
приближение материальной точки. |
||||
|
|
|
|
|
C |
Рассмотренный выше пример с по- |
|
|
x |
|
|
ступательным движением твердого те- |
|||
|
â |
||||||
Рис. 2.8 |
ла — не единственный, когда при опи- |
|
сании движения «большого» тела его |
||
|
можно заменить материальной точкой. Замена «реального» тела на материальную точку может быть оправдана и во всех тех случаях, когда в рамках поставленной задачи влиянием размеров тела можно пренебречь. Например, при вычислении траектории движения Земли вокруг Солнца можно пренебречь ее вращением вокруг своей оси, а также ее размерами, т. к. они малы по сравнению с расстоянием до Солнца. В результате положение Земли в пространстве будет определяться одной точкой и описание ее движения значительно упростится.
Имеется еще одна очень важная причина, почему приближение материальной точки играет в механике исключительную роль. Дело в том, что тело любого размера и любой формы можно представить как совокупность очень малых его частей, взаимодействующих друг с другом. Каждую из таких частей-частичек можно рассматривать как материальную точку и, следовательно, задачу о движении любого тела можно свести к задаче о движении совокупности материальных точек. И мы увидим в дальнейшем, что именно такой прием используется, например, при нахождении законов вращательного движения твердого тела и законов движения жидкости. Из всего вышесказанного следует, что приближение материальной точки (или, как говорят иногда, модель материальной точки) лежит в основе классической механики.
2.4. Преобразования Галилея и закон сложения скоростей
Остановимся теперь на вопросе о том, как изменяется скорость и ускорение материальной точки для наблюдателя, который переходит из одной системы отсчета в другую, движущуюся относительно первой. Так, например, если космическую ракету
2.4 ] |
Преобразования Галилея и закон сложения скоростей |
39 |
|||||||
запускают с поверхности Земли, то ее скорость относительно |
|||||||||
Солнца определится правилом, по которому следует сложить |
|||||||||
скорость ракеты относительно Земли и скорость самой Земли |
|||||||||
относительно Солнца. |
|
|
|
|
|
|
|||
Принципиальный ответ на наш вопрос следует из того факта |
|||||||||
(являющегося обобщением огромного массива опытных данных), |
|||||||||
что положение точки в пространстве и, соответственно, ее |
|||||||||
скорость и ускорение представляются векторными величинами. |
|||||||||
Тогда правило сложения векторов дает |
|
|
|
|
|||||
|
|
|
1 2 2 |
2 1 |
2 2 |
, |
|||
|
1 |
2 |
|
|
|
2 |
2 |
2 |
|
или, что то же, |
|
|
|
|
|
|
|
||
|
|
1 2; |
1 2 |
|
|
||||
Рассмотрим этот вопрос подробнее. Пусть имеются две си- |
|||||||||
стемы отсчета, движущиеся друг относительно друга с постоян- |
|||||||||
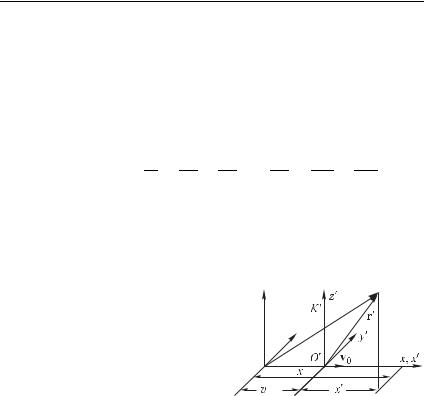
ной скоростью 0 (рис. 2.9). Систему, обозначенную на рисунке |
|||||||||
буквой , будем условно счи- |
|
|
|
|
|
||||
тать неподвижной. Тогда вторая |
|
z |
|
r |
|
||||
система будет двигаться рав- |
K |
|
|
|
|
||||
номерно и прямолинейно. Коор- |
|
y |
|
|
|
||||
динатные оси обеих систем вы- |
|
|
|
|
|||||
|
|
|
|
|
|||||
берем так, чтобы оси и |
O |
|
|
|
|
||||
совпадали, а оси и и оси |
|
|
|
|
|||||
|
|
|
|
|
|||||
и были бы параллель- |
|
0 t |
|
|
|
||||
ны друг другу. Пусть координа- |
|
|
|
|
|||||
|
|
|
|
|
|||||
ты некоторой движущейся мате- |
|
|
Рис. 2.9 |
|
|||||
риальной точки в системе |
|
|
|
|
|
||||
равны , , , а в системе — , , . Время начнем от- |
|||||||||
считывать с того момента, когда начала координат обеих систем |
|||||||||
совпали. Установим сначала связь между координатами нашей |
|||||||||
движущейся точки в системах и , а потом определим связь |
|||||||||
между скоростями в разных системах. Как видно из рисунка 2.9, |
|||||||||
|
0 . Очевидно |
также, |
что |
и . Одно из |
|||||
основных положений классической механики, обобщающее как |
|||||||||
повседневный опыт, так и огромный массив экспериментальной |
|||||||||
информации, утверждает, что при |
время абсолютно, т. е. |
||||||||
в обеих наших системах время течет одинаково: . В резуль- |
|||||||||
тате получаем четыре соотношения: |
|
|
|
|
|||||
0 , , , , |
(2.15) |
называемых преобразованиями Галилея (по имени итальянского физика и астронома Галилео Галилея (1564–1642)).
Помня, что скорость — это производная радиуса-вектора по времени, найдем связь между скоростями точки в обеих

40 Введение в кинематику [ Гл. 2
системах, продифференцировав соотношения (2.15) по времени:
|
|
|
0, |
|
, |
|
, |
|
|
|
|
|
|
|
|
то есть соотношения между проекциями скоростей имеют вид
|
, |
, |
|
0 |
|
|
|
Последние формулы эквивалентны следующему соотношению между вектором скорости по отношению к системе и вектором скорости по отношению к системе :
0 |
(2.16) |
Продифференцируем по времени равенство (2.16). Учитывая, что 0 постоянна, получим
|
, или |
(2.17) |
|
|
|
|
|
Другими словами, ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга равномерно и прямолинейно, одинаково.
Вопросы и задачи
1.Сколько степеней свободы у материальной точки? Сколько степеней свободы у велосипеда?
2.Придумайте задачу, когда при рассмотрении движения велосипеда его можно считать материальной точкой.
3.Вычислите ускорение Земли при ее движении вокруг Солнца, считая ее орбиту круговой, и сравните это ускорение с ускорением свободного падения на поверхности Земли.
Ответ: 6 10 4
4.Начертите приближенно траекторию движения относительно Солнца какого-либо тела, покоящегося на экваторе Земли.
5.На рис. 2.10 дан график зависимости скорости некоторого тела от времени. Постройте графики ускорения этого тела и пройденного им пути.
v, ì/ñ |
|
|
|
|
|
|
a |
|
1 |
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
t, c |
|
1 |
|
|
|
|
|
|
|
|
Рис. 2.10 Рис. 2.11
6. Шар радиуса катится по горизонтальной плоскости без проскальзывания с ускорением . Определите ускорение точки (рис. 2.11) в момент времени, когда скорость тела равна .
Ответ: 2 2 2 .
