
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf3.4 ] |
Понятие импульса. Третий закон Ньютона |
51 |
Фундаментальным законом природы является закон сохранения импульса: векторная сумма импульсов всех тел замкнутой системы в инерциальной системе отсчета не изменяется со временем, хотя каждый из импульсов по отдельности может
с течением времени испытывать существенные изменения. Ecли замкнутая система состоит из ! тел, то закон сохранения импульса можно сформулировать в виде соотношения
|
|
(3.9) |
|
1 |
1 |
2 |
2 |
1
Значение входящей в закон сохранения (3.9) константы (инварианта) может быть различным, и оно определяется начальными условиями, то есть значениями импульcов всех тел в момент образования замкнутой системы тел.
Покажем теперь, что закон сохранения импульса, во-первых, дает возможность измерить массу любого тела путем сравнения ее с массой выбранного эталонного тела, и, во-вторых, позволяет выяснить физический смысл массы как особого свойства всех частиц нашего мира. Для этого рассмотрим простейший случай, когда замкнутая система состоит всего из двух взаимодействующих тел. Тогда закон сохранения импульса (3.9) принимает вид
1 1 2 2 |
(3.10) |
Характер взаимодействия между телами не играет роли — это может быть звезда, вокруг которой вращается единственная планета, или два различных сталкивающихся резиновых мячика, воздействием на которые со стороны других тел можно по каким-то причинам пренебречь. Интересно отметить, что векторное равенство (3.10) может быть изображено в виде треугольника (см. рис. 1.3 б), т. е. в любой системе отсчета векторы скоростей частиц в любой момент времени лежат в одной плоскости.
Рассмотрим два момента времени: один — непосредственно перед столкновением, а другой — сразу после столкновения. Так как суммарный импульс при столкновении сохраняется, то мы получаем из (3.10)
1 1 до 2 2 до 1 1 после 2 2 после ,
где слева стоят значения скоростей до столкновения, а справа — непосредственно после столкновения.
Последнее равенство удобнее представить как
1 1 после 1 до 2 2 после 2 до ,
или в более компактной форме:
|
|
1 |
|
|
(3.11) |
1 |
|
2 |
2 |
|

52 |
Законы Ньютона |
[ Гл. 3 |
В последнем соотношении 1 и 2 означают изменения скоростей соответствующих тел в результате их столкновения. Эти изменения скоростей являются, как и сами скорости, векторными величинами, и направлены, как следует из (3.11), по одной прямой в противоположные стороны. Для модулей этих изменений скоростей 1 и 2 получаем из (3.11) равенство
1 1 2 2 |
(3.12) |
Важно отметить, что величины 1 и 2 могут быть измерены опытным путем.
А теперь представим себе, что массу одного из сталкивающихся тел (например, 2) мы условились считать эталоном массы ( 2 э). Проводя тогда наблюдения за столкновением произвольного тела с эталонным телом, мы всегда сможем выразить с помощью соотношения (3.12) его неизвестную до этого массу через эталонную массу э и через измеренные на опыте изменения скоростей:
ээ
На практике массу тела чаще измеряют, используя другие соотношения. Важная роль закона сохранения импульса для определения массы тела состоит в том, что при этом определении не требуется вводить никаких других величин, которые были бы нам до этого неизвестны. Необходимо лишь условится об эталонной единице массы.
Обсудим еще раз вопрос о том, какое физическое свойство тел характеризует их масса — свойство, которое бы находило отражение в наших повседневных контактах с различными предметами. Из соотношения (3.12) следует, что чем больше масса тела, тем меньше оно изменяет свою скорость в процессе взаимодействия. Хорошо всем знакомое свойство тел оказывать сопротивление при попытках привести его в движение или изменить величину или направление его скорости называется «инертностью». И мы видим, что чем больше масса тела, тем сильнеe оно «сопротивляется» изменению его скорости. Таким образом, масса характеризует «инерционную способность» тела,
и можно, следовательно, сказать, что масса тела — это мера инертности тела, в принципе она может быть измерена на основе закона сохранения импульса. Во всяком случае, это
единственный способ «взвешивания» элементарных частиц. Последним по порядку, но не по значению, будет вывод из за-
кона сохранения импульса классической формы третьего закона Ньютона (3.3). Рассмотрим замкнутую систему двух тел 1 и 2. Продифференцируем по времени условие постоянства их полного

3.5 ] Вопросы 53
импульса 1 2 :
1 2 0,
а далее, учитывая для каждого из них закон (3.7), приходим к окончательному результату:
12 21,
где 12 — сила, действующая на тело 1 со стороны тела 2, и наоборот. Мы смогли указать точный «адрес» каждой силы, поскольку тел в нашей системе всего два. Поэтому то, что нами получено, еще не полностью эквивалентно (3.3). Доказательство в случае произвольного числа тел не столь математически очевидно; его проще оказывается провести «в обратную сторону»:
|
|
0, |
если |
||
|
|
||||
|
|
|
|
||
|
|
|
подразумевает, что тело |
||
(Условие второго суммирования " |
|||||
само себя ни тянуть, ни толкать в инерциальной системе отсчета не может, т. е. 0).
Хотя закон сохранения импульса, как мы уже отметили, более универсален с точки зрения современной физики, традиционный третий закон Ньютона (3.3) в классической механике также занимает достойное место, особенно в статике — науке о равновесии физических тел и систем тел.
Вопросы
1.Сформулируйте закон сохранения импульса.
2.Что такое масса и что такое сила?
3.Какой тип фундаментальных взаимодействий лежит в основе сил тре-
ния?
4.Что такое вес тела?
5.Какова размерность импульса?
6.Можно ли вывести закон инерции (3.1) из второго закона Ньютона
(3.2)?
7.Является ли масса скалярной величиной?
8.Что общего между абсолютно свободным телом и замкнутой системой
тел?
Г л а в а 4
ПРИМЕРЫ ПРИЛОЖЕНИЙ
ЗАКОНОВ НЬЮТОНА
4.1. Исследование закона движения материальной точки
Исследование закона движения означает получение временн´ой зависимости всех координат, определяющих положение тела в пространстве. В частности, для материальной точки это три координаты, определяющие зависимость . Как мы уже знаем, второй закон Ньютона в формулировке (3.4) представляет собой уравнение, содержащее не сам радиус-вектор, а его вторую производную по времени. И если зависимость силы от положения
материальной точки известна, то есть известна зависимость F от r, то соотношение (3.4) представляет собой дифференциальное уравнение, где подлежащая определению функция r(t)
входит под знаком производной. Если нам известна зависимость действующей на тело силы от его положения в пространстве и если мы знаем положение тела и его скорость в какой-то момент времени, то мы можем с помощью уравнения (3.4) вычислить его положение и скорость в любой из последующих моментов времени. Следовательно, второй закон Ньютона дает возможность предсказать всю траекторию движения материальной точки в зависимости от времени, если известны начальные условия: начальное значение радиуса-вектора 0 и начальное значение скорости 0 .
Заметим, что бросая камень или мяч в цель, человек интуитивно использует приобретенную из опыта информацию о связи начального положения руки и ее начальной скорости с последующей траекторией полета брошенного предмета. Это приобретенное на опыте знание человечество использовало с первых шагов своей эволюции, но только после формулировки второго закона Ньютоном в XVII столетии у человека появилась возможность перейти от интуитивного предсказания характера движения тел к точному расчету, и это послужило одной из причин резкого ускорения технического прогресса на нашей планете.
А теперь покажем, как второй закон «работает» в качестве инструмента для вычисления траекторий движения. Пусть перед нами стоит задача вычислить в зависимости от времени
4.1 ] |
Исследование закона движения материальной точки |
55 |
внекоторой инерциальной системе траекторию движения тела массы , которое можно рассматривать как материальную точку (рис. 4.1). Величина и направление силы, действующей на тело
вкаждой точке пространства, предполагаются известными, то
|
|
|
m |
F0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
r0 |
v0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
à |
|
|
|
||
|
|
|
t0 |
t1 |
t2 |
t3 |
|
t |
|
|
|
|
|
t |
t |
t |
|
|
|
|
|
|
|
|
|
v1 |
|
|
|
|
|
|
|
r v0 t |
|
v |
F0 |
t |
|
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
|
|
|
|
z |
r0 |
|
|
v0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
á |
|
|
|
||
|
|
|
t0 |
t1 |
t2 |
t3 |
|
t |
|
|
|
|
|
t |
t |
t |
|
|
|
F1 v1
z
m
x |
y |
|
|
|
â |
|
t0 |
t1 |
t2 |
t3 |
t |
|
|
t |
t |
t |
|
Рис. 4.1
есть известна — зависимость этой силы от радиуса-вектора тела. Такая ситуация встречается очень часто. Один из самых простых примеров — движение вблизи поверхности Земли под действием силы тяжести, которая везде равна по величине и направлена к поверхности.
Начальные условия для движения рассматриваемого тела заключаются в том, что в некоторый начальный момент времени

56 |
Примеры приложений законов Ньютона |
[ Гл. 4 |
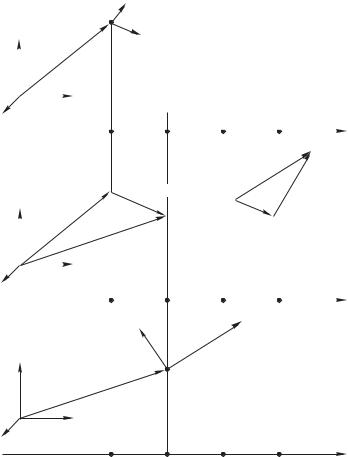
0 нам, во-первых, известно положение тела в пространстве (то есть его начальный радиус-вектор r0) и, во-вторых, известна его начальная скорость 0. Эта начальная ситуация изображена на рис. 4.1 а, где также представлена шкала времени, которое мы разбили на малые интервалы , разделяющие следующие друг за другом моменты 1, 2, 3, и так далее. Будем подразумевать, что интервал будет в конечном итоге выбираться сколь угодно малым, то есть устремлен к нулю. Это позволит нам использовать физические величины (скорость, ускорение), выраженные через производные по времени от соответствующих функций. Но для наглядности будем пока представлять просто как очень малый временной интервал.
Теперь покажем сначала, что, зная 0, 0 и значение действу-
ющей на тело в точке 0 силы 0, мы можем с помощью второго закона Ньютона определить 1 и 1 — новое положение тела и его новую скорость через интервал времени . Учитывая,
что мы подразумеваем под сколь угодно малый интервал, перепишем определение скорости в виде
|
(4.1) |
|
|
Если применить это соотношение в точке 0, то из него мы сразу получаем 0 — изменение начального радиуса-вектора тела за интервал , то есть
0 0
А зная это изменение начального положения тела, мы можем найти его новое положение, то есть новое значение радиуса-
вектора в момент 1 (см. рис. 4.1 б):
|
1 |
|
|
|
|
|
(4.2) |
|
0 |
0 |
0 |
0 |
|
|
Найдем теперь с помощью второго закона новое значение скорости 1 в момент 1. Используем соотношения
, |
|
(4.3) |
|
|
|
в точке 0 в момент 0 и определим из них приращение скорости:
0 |
0 |
|
(4.4) |
|
|
||||
|
|
|
Зная 0, получаем для нового значения скорости в точке 1
в момент 1: |
|
|
|
0 |
|
(4.5) |
|
|
|
0 |
|
||||
|
|||||||
1 |
0 |
0 |
|
|
|
Итак, мы сумели, стартуя с начального положения тела, найти его новое положение на траектории 1 и новую скорость 1 в момент 1. Но теперь мы пришли к ситуации, полностью аналогичной начальной (см. рис. 4.1 в). И так как значение

4.2 ] Движение материальной точки под действием постоянной силы 57
силы в новой точке 1 нам известно, то, продолжая вычисления точно тем же способом, мы шаг за шагом найдем положение и скорость тела во все последующие моменты времени 2, 3, и так далее. Последнее и означает, что, зная начальное положение
иначальную скорость материальной точки, можно с помощью второго закона Ньютона вычислить, то есть предсказать, всю последующую траекторию ее движения. На практике вычисление траектории осуществляют одним из двух способов. Во-первых, можно использовать компьютер, «поручив» ему проделывать всю ту процедуру последовательного нахождения точек траектории, о которой мы говорили выше. Для этого компьютеру надо только задать величину «временного шага» и ввести в компьютер программу вычислений, определяемых соотношениями (4.1)–(4.5). Во многих случаях, однако, можно обойтись без компьютера. Мы говорили уже, что второй закон Ньютона является дифференциальным уравнением, конкретный вид которого зависит от физических условий задачи (фактически, от характера зависимости действующей на тело силы от его положения в пространстве — ). Решение такого уравнения часто удается найти, используя хорошо известные правила интегрирования
идифференцирования, а в некоторых случаях (составляющих большую часть задач в студенческих задачниках) даже с помощью элементарной алгебры. Некоторые примеры таких решений мы рассмотрим в последующих параграфах.
4.2. Движение материальной точки под действием постоянной силы
Перейдем сейчас от обсуждения общих свойств второго закона Ньютона как средства для вычисления траекторий к рассмотрению конкретных задач и конкретных движений, которые можно детально исследовать с помощью этого основного уравнения механики. Как и при изучении любого явления, разумно начать с рассмотрения таких движений, которые, с одной стороны, допускали бы относительно простое математическое решение задачи, а, с другой, имели бы достаточно большое практическое значение.
Закон движения тела, то есть зависимость его радиуса-векто- ра от , определяется характером действующей на него силы и является, согласно второму закону Ньютона, решением уравнения (4.3).
Вслучае, когда на тело никакие силы не действуют, то есть
0, решением уравнения (4.3) является движение с постоянной скоростью . Это простейший тип движения — свободное движение. Следующий по сложности тип движения —
58 |
Примеры приложений законов Ньютона |
[ Гл. 4 |
это такое движение, при котором действующая на тело сила хотя и не равна нулю, но не меняется по величине и направлению при перемещении тела. Это означает, что правая часть первого из уравнений (4.3) является константой. Любое уравнение решается проще, когда входящие в него коэффициенты остаются постоянными, не зависящими от времени и координат, так что этот тип движения наверняка окажется наименее сложным с точки зрения его математического исследования. С другой стороны, движение под действием постоянной силы является очень важным с практической точки зрения и часто встречается в повседневной жизни.
Прежде всего, к такому типу движения относится при определенных условиях движение под действием силы тяжести. Сила тяжести, как и любая сила, является векторной величиной. Примем упрощающее предположение, что ее модуль постоянен и равен . Но так как эта сила направлена к центру Земли, то ее направление в разных точках земной поверхности различно. Однако при исследовании движений тел, перемещающихся на расстояния, которые намного меньше радиуса Земли ( 6 000 км), можно пренебречь кривизной земной поверхности и с хорошей точностью считать, что сила тяжести не меняет своего направления, оставаясь перпендикулярной этой поверхности. В этих условиях сила тяжести может рассматриваться постоянной как по модулю, так и по направлению. Помимо силы тяжести, с постоянными силами приходится часто сталкиваться при рассмотрении работы различных технических устройств, когда их различные детали испытывают действие постоянных сил со стороны других деталей.
Мы подробно разберем случай движения тела под действием постоянной силы на конкретном примере определения закона движения брошенного камня или снаряда, вылетевшего из ствола орудия. Какой вид имеет траектория камня? От чего зависит дальность полета? Древнегреческий философ и ученый Аристотель (384–322 до н. э.) утверждал, например, что на начальном участке траектория брошенного под углом к вертикали тела является прямой линией, и это, вроде бы, подтверждалось непосредственными наблюдениями. Потребовалось почти два тысячелетия, чтобы понять, что траектория на самом деле является криволинейной на всех участках полета.
Изучение движения брошенного под углом к вертикали тела включает в себя несколько этапов, характерных для решения
большинства задач механики.
Первый этап — определение типа движения. В нашем случае это означает выяснение вопроса о том, можем ли мы пренебречь влиянием размеров тела при решении задачи, то есть, можно ли рассматривать его движение, как движение материаль-
4.2 ] Движение материальной точки под действием постоянной силы |
59 |
||
ной точки, и, следовательно, применять второй закон Ньютона |
|||
(4.3). В общем случае на брошенное тело, помимо силы тяже- |
|||
сти, действует сила, порожденная обтеканием воздуха, которое |
|||
зависит от размеров и формы тела. Эта зависимость может силь- |
|||
но усложнить решение задачи и на практике может приводить |
|||
к весьма замысловатым траекториям полета тела. Вспомним хотя |
|||
бы о движении изобретенного австралийскими аборигенами бу- |
|||
меранга, который после броска возвращается к охотнику. Однако |
|||
во многих случаях эффектами обтекания можно с достаточной |
|||
точностью пренебречь. Именно такой случай мы и будем рас- |
|||
сматривать, то есть мы воспользуемся для решения основным |
|||
уравнением движения материальной точки (4.3). |
|
|
|
Второй этап — физическая формулировка задачи: выбор |
|||
системы отсчета, определение действующих сил и началь- |
|||
ных условий. Рассмотрим случай, когда тело начинает движение |
|||
в некоторой точке на поверхности Земли. В качестве системы |
|||
координат выберем декартову систему, начало которой естествен- |
|||
но поместить в эту точку. Оси , , |
z |
m |
|
расположим так, чтобы ось бы- |
|
||
|
|
|
|
ла перпендикулярна поверхности, а век- |
y |
mg |
|
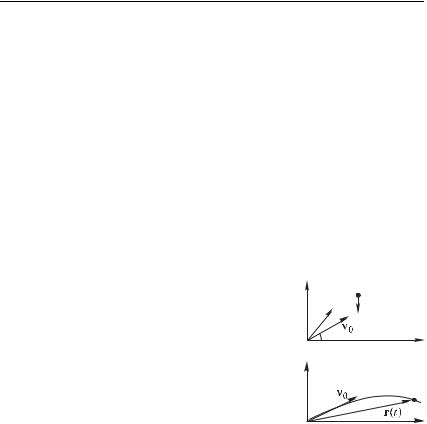
тор начальной скорости 0 лежал, как на |
|
|
|
рис. 4.2 а, в плоскости . Начальный |
|
|
|
модуль скорости 0 и ее начальное направ- |
O |
à |
x |
|
|
||
ление, то есть угол # между 0 и осью , |
z |
|
|
определяются теми условиями и причина- |
|
|
|
ми, которые приводят камень или снаряд |
|
|
|
в движение. Это, например, расположение |
|
|
|
и скорость движения руки при бросании |
O |
á |
x |
камня или наклон орудия и мощность по- |
|
|
|
|
Рис. 4.2 |
|
|
рохового заряда. |
|
|
|
|
|
|
|
Система отсчета, связанная с поверхностью Земли, не явля- |
|||
ется, строго говоря, инерциальной, так как любая точка поверх- |
|||
ности движется с ускорением, обусловленным вращением Земли |
|||
вокруг своей оси и вокруг Солнца. Но для многих практиче- |
|||
ских задач этот эффект «неинерциальности» является несуще- |
|||
ственным, и мы будем полагать, что и в нашей задаче этим |
|||
эффектом можно пренебречь и считать выбранную систему от- |
|||
счета инерциальной. В инерциальной системе отсчета справедлив |
|||
второй закон Ньютона (4.3), где теперь под F подразумевается |
|||
постоянная сила тяжести. Мы изобразили эту силу на рис. 4.2 а |
|||
для некоторого произвольного момента времени после начала |
|||
движения, поместив тело массы в некоторой произвольной |
|||
точке над поверхностью. Истинное положение тела в различные |
|||
моменты времени, то есть траекторию его движения, мы сможем |
|||
определить только после окончательного решения задачи. |
|
||
60 |
Примеры приложений законов Ньютона |
[ Гл. 4 |
Третий этап — математическая формулировка задачи: запись уравнений, соответствующих физической формулиро-
вке. Уравнение (4.3) содержит в качестве неизвестных векторные величины и . Поэтому оно фактически представляет собой совокупность трех уравнений для трех проекций вышеупомянутых величин. Для проекций радиуса-вектора тела введем обозначения: , , . Взяв проекции на оси координат от левой и правой частей уравнения (4.3), мы получаем три уравнения:
0, |
; |
0 0, |
0 0 #, (4.6) |
|
|
|
|
|
|
0, |
; |
0 0, |
0 0, |
(4.7) |
|
|
|
|
|
, |
; |
0 0, |
0 0 # |
(4.8) |
|
|
|
|
|
Справа от каждого из уравнений записаны начальные условия, являющиеся неотъемлемыми элементами физической и математической формулировки задачи. Знак «минус» перед в последнем уравнении отражает тот факт, что сила тяжести направ-
лена в отрицательном направлении оси .
Четвертый этап — математическое решение задачи. Теперь предстоит чисто «техническая» работа — решение сформулированных ранее уравнений с помощью известных в математике приемов и методов. В произвольном случае уравнения могут оказаться столь сложными, что их решение невозможно без привлечения компьютерной техники. В нашем же, относительно простом случае, решение уравнений (4.3), удовлетворяющее начальным условиям, может быть найдено на основе элементарных знаний о правилах вычисления производных от простейших функций.
Рассмотрим, например, уравнение (4.8). Составляющая скорости имеет вид: Константу определяем из условия 0 0 # Интегрируем еще раз:
0 # 2 2 Новую константу определяем из условия0 0 Аналогично находятся решения уравнений (4.6), (4.7), так что окончательно решение выглядит следующим образом:
0 #, 0, 0 # |
2 |
(4.9) |
|
2 |
|
Найденные выражения определяют зависимость от времени всех трех проекций радиуса-вектора тела, движущегося под действием силы тяжести. Тем самым задача о нахождении траектории движения решена. Для того чтобы ответить на вопрос, к какому типу геометрических кривых (гипербола, парабола и т. п.) относится найденная траектория, достаточно выразить через в первом из равенств (4.9) и подставить результат в вы-
