студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

4.2 ] Движение материальной точки под действием постоянной силы 61

ражение для . Это дает следующее уравнение траектории

Из геометрии известно, что это соотношение представляет собой уравнение параболической кривой, и следовательно, ни на одном из участков полета тела его траектория не является прямой линией (см. рис. 4.2 б).

Из соотношения (4.10) можно определить, например, дальность полета тела п. При падении на поверхность 0, и из этого условия находим с помощью (4.10)

Пятый этап — проверка полученного решения. Этот, последний, этап является неотъемлемым и очень важным элементом решения всякой физической задачи. Самым очевидным способом проверки является поэтапное повторение всего процесса решения. Но помимо этого существуют специальные приемы, позволяющие быстро проверить полученный ответ на наличие

в нем грубых ошибок. Наиболее известны два таких приема.

Прием первый — проверка ответа по размерности. Речь здесь идет о том, что полученный результат должен удовлетворять правилам размерности, о которой мы говорили в предыдущей главе. Если результатом вычисления является, например, скорость, то и ответ должен иметь размерность скорости. Если вычислялась сила, то ответ должен иметь размерность силы и т. п. В нашем случае размерность полученного ответа правильна:

2

п 0

Прием второй — проверка ответа по заранее очевидным результатам. Часто бывает так, что при некоторых значениях

входящих в задачу физических величин ответ можно «предсказать» заранее, так как он является очевидным. Как правило, результат очевиден для предельных значений каких-либо величин, например, при нулевых или бесконечных значениях времени или расстояния, при нулевой или бесконечной массе и так далее. Проверим этим способом тот же результат (4.11) для дальности полета тела. Очевидно, например, что при нулевой начальной скорости 0 тело останется в исходном положении и дальность полета п должна равняться нулю. Мы видим, что найденноe нами решение удовлетворяет этому условию. Очевидно также, что дальность должна равняться нулю, если начальная скорость направлена строго вертикально, и мы видим в (4.11), что действительно, п 0 при # $ 2. Наконец, очевидно, что в отсутствие силы тяжести (то есть при 0) дальность полета должна

быть бесконечной, и мы видим, что наш ответ удовлетворяет и этому условию. Как и в случае с размерностью, проведенная выше проверка не дает стопроцентной гарантии отсутствия ошибки (хотя бы, например, в численных коэффициентах). Но она, во всяком случае, страхует от совершения грубых ошибок.

4.3. Реактивное движение

Во многих случаях траекторию и временные´ характеристики движения материальной точки можно установить, вообще не об-

ращаясь ко второму закону Ньютона. Примером такой ситуации может быть реактивное движение, которое осуществляется за

счет выброса части общей массы тела в каком-либо направлении. Именно так движутся, например, космические корабли и обычные осветительные ракеты.

Рассмотрим задачу о реактивном движении для наиболее простого случая, когда ракета движется в дальнем космосе, так что воздействием на нее Земли и других планет можно пренебречь. Решение всякой задачи о движении начинается, как мы уже знаем, с выбора системы отсчета. В качестве таковой мы выберем некоторую инерциальную систему, конкретная привязка которой для данной задачи несущественна — это может быть си-

газов) выбрасывается из задней части ракеты таким образом, что ракета и выброшенное топливо движутся по одной прямой, совпадающей с осью .

Скорость выброса топлива относительно корпуса ракеты отн считается известной — она определяется конструктивными особенностями и зависит от типа топлива, формы сопла, температуры сгорания топлива в сопле и т. д. Будем далее предполагать, что эта скорость отн остается во время полета постоянной. Наша цель состоит в том, чтобы определить, по какому временн´ому закону будет перемещаться ракета и как будут меняться со временем ее скорость и полная масса. После выбора системы отсчета и задания физических условий задачи необходимо выяснить, можем ли мы рассматривать движение ракеты как дви-

жение материальной точки, то есть считать его не зависящим от размеров ракеты. Только в этом случае мы сможем использовать, например, закон сохранения импульса. В нашем случае это приближение будет справедливо при условии, что ракета или реактивный снаряд не будет «кувыркаться» в полете. Не останавливаясь на формальном описании этого свойства (обусловленного динамикой твердого тела конечных размеров), ограничимся ссылкой на то обстоятельство, что аппарат, сконструированный должным образом, в полете устойчив.

Чтобы понять, какие именно законы движения нам следует использовать, остановимся коротко на принципе реактивного движения. Этот принцип очень прост. Ракета воздействует определенным образом на выбрасываемое из сопла вещество (газы). Выбрасываемое вещество, в свою очередь, воздействует на ракету и увеличивает ее скорость в противоположном направлении. Если воздействием всех других тел можно, как в нашем случае, пренебречь, то ракета вместе с выброшенным веществом является замкнутой системой. Суммарный импульс такой системы не меняется во времени, и именно закон сохранения импульса лежит в основе решения нашей задачи.

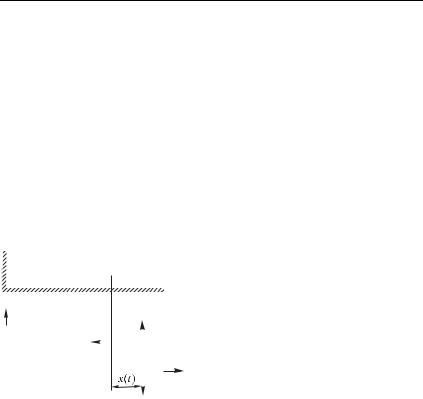
Предположим, что за малый промежуток времени масса и скорость ракеты получат приращения и (величина отрицательна). На рис. 4.3 б изображена ситуация к моменту времени : ракета имеет к этому моменту полную массуи скорость , в то время, как выброшенная за время масса газа газ летит относительно выбранной системы отсчета со скоростью газ отн. Такая величина получается по правилу сложения скоростей, если учесть, что скорость ракеты направлена в положительном направлении оси , а скорость выброшенного топлива — в отрицательном.

Из закона сохранения импульса следует, что суммарный импульс ракеты и топлива имеет одно и тоже значение в моментыи , то есть

Если устремить промежуток времени , а с ним и приращения и к нулю, то в (4.12) можно отбросить произведение как величину малую по сравнению со слагаемыми, содержащими малые приращения в первой степени (как бесконечно малую высшего порядка). Ввиду сохранения массыгаз 0. Пользуясь этим, получаем из (4.12)

где мы при переходе к бесконечно малым пределам заменили, как

принято в математике, конечные приращения на дифференциалы соответствующих величин.

Равенство (4.13) — это соотношение между бесконечно малыми величинами. Для того чтобы получить соотношение между конечными, доступными измерению, значениями скорости ракеты и ее массы, следует просуммировать левую и правую части равенства (4.13). Такое суммирование бесконечно малых выражается, как известно, операцией интегрирования:

отн ,

где мы вынесли постоянное значение скорости газов отн за знак интеграла. Воспользовавшись известными правилами интегрирования, получаем

отн %

Значение постоянной интегрирования % определяется начальными условиями. Допустим, что в начальный момент времени скорость ракеты равна нулю, а ее масса равна 0. Тогда предыдущее уравнение дает

Соотношение (4.14) называют формулой Циолковского по имени К.Э. Циолковского (1857–1935).

Формула Циолковского позволяет рассчитать запас топлива, необходимый для сообщения ракете определенной скорости . Допустим, например, что ракете надо сообщить «первую космическую скорость», то есть такую скорость, чтобы она начала двигаться вокруг Земли по окружности. Эта скорость приблизительно равна 8 км/с (в дальнейшем мы покажем, почему первая космическая скорость равна именно такой величине). В современных ракетах скорость газовой струи достигает нескольких километров в секунду. Если считать скорость газовой струи равной отн 2 км/с, то из формулы Циолковского получается, что для достижения 8 км/с необходимо, чтобы отношение конечной массы ракеты к ее начальной массе было равно 0 54,6. Это означает, что почти 98 % массы ракеты приходится на топливо.

Не представляет особых трудностей обобщение проведенного рассмотрения на случай переменной во времени скорости истечения газов. Для этого уравнение (4.13) надо просто разделить на

.Учтем также, что все импульсы и их приращения, входящие

в(4.12), суть истинные векторы, и придадим окончательному

66 Примеры приложений законов Ньютона [ Гл. 4

важнейшие свойства окружающих нас тел, таких как прочность или способность проводить тепло.

Колебательное движение может иметь очень сложный вид. Мы рассмотрим простейший тип — гармонические колебания,

то есть такие колебания, при которых колеблющаяся величина (например, отклонение маятника) изменяется со временем по закону синуса или косинуса. Этот вид колебаний,

несмотря на свою простоту, особенно важен по двум причинам: во-первых, многие колебания в природе и технике очень близки к гармоническим, и, во-вторых, периодические процессы с любой другой зависимостью от времени могут быть представлены, как наложение (суперпозиция) истинно гармонических колебаний.

Oсновные особенности гармонических колебаний мы рассмотрим на примере колебаний соединенного с пружиной тела массы , находящегося на горизонтальной поверхности, трением о

траектории второй закон Ньютона. Как и в предыдущем параграфе, постановку вопроса об адекватности такого приближения и возможных отклонениях от него нам придется отложить до знакомства с динамикой твердого тела конечных размеров.

Следующий этап — выбор системы координат, определение действующих на тело сил и начальных условий. В нашей задаче естественно выбрать декартову систему координат, у которой, например, ось направлена вдоль пружины, а начало координат соответствует «равновесному» положению тела, когда пружина не растянута и не сжата.

Мы должны также определиться с упругими свойствами пружины: это не может быть гибкая пружина, работающая только на растяжение, но провисающая при сжатии. Мы предположим, что пружина симметричным образом реагирует на нагрузку любого

знака:

, где — коэффициент жесткости пружины. При & 0 пру-

жина растянута и упругая сила направлена в сторону, про-

где и две произвольных пока константы, для определения которых как раз будет достаточно двух начальных условий нашей задачи.

Из начальных условий (4.17) с учетом (4.19) имеем два соотношения:

0 0 , 0 0 0

Из второго из этих соотношений следует: $ 2, а тогда из первого соотношения имеем 0. Таким образом, удовлетворяющее начальным условиям решение нашей задачи имеет вид

Итак, отклонение тела от положения равновесия меняется со временем по синусоидальному закону, то есть тело со-

колебаний называется амплитудой колебаний. Амплитуда — постоянная положительная величина. В нашей задаче амплитуда

равна 0 — начальному отклонению тела от равновесного положения. Аргумент синуса 0 называется фазой колебания,

а значение фазы при 0, то есть константа , называется начальной фазой колебания. В нашей задаче начальная фаза

равна $ 2.

Поскольку синус — периодическая функция с периодом 2$, различные положения тела, совершающего гармонические колебания, повторяются через такой промежуток времени , за ко-

торый фаза колебаний получает приращение 2$ (см. рис. 4.5 а). Этот промежуток времени называется периодом колебаний.

Число колебаний в единицу времени называется частотой колебаний (. Чтобы найти связь между ( и продолжительно-

стью одного колебания , следует, очевидно, поделить единицу времени на :

За единицу частоты принимается частота таких колебаний, пе-

риод которых равен одной секунде (одно колебание в секунду). Эту единицу называют герцем (Гц). Частота в тысячу герц называется килогерцем (кГц), в миллион герц — мегагерцем (МГц).

Из (4.21) следует, что

Таким образом, 0 равно числу колебаний за 2$ секунд. Величину 0 называют круговой или циклической частотой. Она

связана с обычной частотой ( соотношением

Для нашей конкретной задачи о колебаниях тела на пружине по гладкой поверхности значение 0 дается соотношением (4.18), то есть оно определяется массой тела и коэффициентом жесткости пружины. Для других возможных случаев гармонических колебаний их частота, как мы увидим позже, определяется другими физическими величинами. Это может быть, например, масса и размеры маятника, ускорение свободного падения. Для колебаний электрического тока в радиотехнических устройствах циклическая частота зависит от электрических характеристик, таких как индуктивность и емкость.

Колебательное движение обладает одним интересным и практически очень важным свойством, заключающимся в его особой «чувствительности» к дополнительному воздействию на колеблющееся тело со стороны внешней силы, которая сама меняется со временем по гармоническому закону. Чтобы понять основные особенности этого явления, мы рассмотрим то же самое тело на пружине, движение которого мы только что изучали, но только теперь на тело вдоль пружины действует еще внешняя, как принято говорить, «вынуждающая» сила в (рис. 4.6). Пусть ее горизонтальная проекция изменяется со временем по закону:

70 Примеры приложений законов Ньютона [ Гл. 4

Как изменится движение нашего тела в этом случае? Уравнение движения с учетом дополнительной силы примет, очевидно,

Даже без привлечения специальной математики представляет-

жуток времени тело будет совершать колебания с той же частотой, с какой колеблется вынуждающая сила, то есть решение уравнения движения (4.27) примет вид

Подставив это выражение в (4.27), легко убедиться, что мы нашли правильное решение, если амплитуда удовлетворяет соотношению

Определив отсюда , получаем окончательно искомое решение уравнения движения (4.27):

Итак, под действием вынуждающей силы тело совершает гармонические колебания с той же частотой , с которой меняется

сама эта сила. И чем ближе оказывается частота вынуждающей силы к частоте свободных колебаний тела 0 (собственной

частоте), тем больше амплитуда результирующих колебаний тела, а при 0 амплитуда вообще формально становится бесконечной. Для реальных систем амплитуда, разумеется, всегда остается конечной; в нашем случае бесконечность при 0 обусловлена тем, что мы ограничились линейным приближениеми не учли влияния силы трения. При учете трения амплитуда, хотя и резко возрастает, но остается конечной величиной.