
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
6.3 ] Потенциальная энергия взаимодействия. 101
отсчета можно представить в виде
|
" 2 |
|
|
|
|
|
|
2 |
|
|
|
||||||
|
2 |
2 |
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 2 2 |
2 |
(6.12) |
|||
|
|
|
|
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правую часть (6.12) можно представить в виде трех сумм: |
|||||||||||||||||
|
2 |
1 |
|
2 1 |
|
2 |
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
, |
||
2 |
2 |
|
|
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.13) |
|
где P — полный импульс системы материальных точек в новой системе отсчета. Соотношение (6.13) принято называть теоремой Кёнига по имени немецкого физика А. Кёнига (1856–1901). Если же новая система совпадает с ц-системой, то суммарный импульс в ней равен нулю, , а значит, имеет место соотношение (6.11).
В заключение этого параграфа отметим два важных свойства, вытекающих из определения центра масс. Во-первых, частицы в (6.7) можно объединять в какие угодно группы, например:
1 1 2 2 |
1 2 1 1 2 2 |
||||||
1 2 |
|||||||
|
|
|
1 2 |
||||
3 4 |
3 3 |
2 |
4 |
1 2 |
|||
|
|
|
|
|
|||
|
1 |
4 |
|
||||
|
|
|
|
|
|||
Отсюда, как легко сообразить, следует, что центр масс любой системы макроскопических тел может быть найден как центр масс системы материальных точек, в предположении, что масса каждого тела сосредоточена в его собственном центре масс.
И во-вторых, от суммирования в (6.7) нетрудно перейти к интегрированию, если мы вычисляем положение центра масс тела с непрерывным распределением плотности вещества 3 :
3 3
6.3.Потенциальная энергия взаимодействия. Закон сохранения энергии для замкнутой системы
материальных точек
В предыдущей главе мы познакомились с понятиями кинетической и потенциальной энергии для специального и относительно простого типа движения — движения одной материальной точки под действием заданной силы (движение в постоянном силовом поле). Теперь мы познакомимся с тем, как формулируется
102 |
Замкнутая система тел |
[ Гл. 6 |
закон сохранения энергии для более сложного типа движения — движения многих взаимодействующих тел, образующих замкнутую систему.
Начнем с рассмотрения простейшей системы тел — системы, состоящей всего из двух материальных точек, а силу взаимодействия между ними будем полагать потенциальной и зависящей лишь от 1 2 Эта оговорка весьма существенна. Например, сила взаимодействия между заряженными частицами, вообще говоря, непотенциальна и зависит от их скоростей, сила взаимодействия между двумя диполями, даже будучи потенциальной, зависит от ориентации частиц в пространстве и т. д. Запишем уравнения движения рассматриваемых материальных точек в некоторой инерциальной системе координат:
|
1 |
|
, |
1 |
|
12 2 1 1 1 |
|
|
|||
|
2 |
|
(6.14) |
|
|
, |
|
2 |
|
21 2 1 2 2 |
|
|
где по-прежнему 1 и 2 — радиусы-векторы рассматриваемых материальных точек; 1, 2 — их скорости; 1 и 2 — их массы, а 12, 21 — силы, с которыми они действуют друг на друга. Мы предполагаем теперь, что наряду с силами 12 и 21 на тела действуют еще внешние, как говорят, сторонниe, силы 1 и 2 (то есть рассматриваемая система тел не является замкнутой).
Умножим обе части первого из уравнений (6.14) на бесконечно малое перемещение первого тела и обе части второго уравнения на , а затем сложим левые и правые части полученных таким образом соотношений. С учетом того, что 12 21, получаем
|
1 |
|
2 |
|
, |
1 |
|
1 2 |
|
2 21 1 1 2 2 |
|
|
|
где 2 1, и, поскольку 1 1, 2 2, отсюда следует
22
1 1 |
|
2 2 |
|
|
21 |
|
|
|
1 |
|
2 |
(6.15) |
||
|
|
|
|
|
|
|||||||||
2 |
|
2 |
|
|
|
1 |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
||||||
Определим понятие потенциальной энергии взаимодействия:
потенциальной энергией взаимодействия 412 между материальными точками 1 и 2, находящимися на расстоянии друг от друга, называется работа, совершаемая силой взаимодействия при удалении одной из них от другой с расстояния в бесконечность, т. е.
412 вз |
(6.16) |
6.3 ] |
Потенциальная энергия взаимодействия. |
103 |
Определение конкретного выражения для 412 сводится, как мы видим, к вычислению вз для конкретной силы взаимодействия 21, и в следующем параграфе мы покажем в качестве примера, как находится потенциальная энергия гравитационного взаимодействия. Бесконечность в (6.16) принято вводить для определенности; разумеется, при вычислении сил либо работы на конечном участке пути потенциальная энергия, как и в постоянном силовом поле (см. гл. 5), определена с точностью до константы. Если силы взаимодействия между материальными точками являются потенциальными, то работа не зависит от пути. Это, в частности, справедливо для важного частного случая центральных сил:
|
|
12 |
; |
|
|
(6.17) |
12 |
|
# |
1 |
2 |
|
Здесь — единичный вектор, так называемый орт направления. Закон взаимодействия (6.17) никогда не бывает справедлив в точности, но очень во многих случаях используется как достаточно хорошее приближение к реальности.
Подчеркнем одно отличие потенциальной энергии взаимодействия между двумя материальными точками 412 от потенциальной энергии одной материальной точки в постоянном силовом поле , , о которой шла речь в гл. 5. Потенциальная энергия взаимодействия двух материальных точек зависит только от расстояния между ними — если, конечно, не вступают в игру ориентационные координаты, скажем, направление дипольных моментов частиц (о чем мы будем говорить в следующем разделе курса). Чтобы подчеркнуть это различие, потенциальную энер-
гию взаимодействия двух материальных точек называют обычно просто энергией взаимодействия, и мы так и будем ее называть
в дальнейшем.
Из соотношения (6.15) следует связь между работой и приращением кинетической энергии при бесконечно малых перемещениях:
Æвз Æвн |
(6.18) |
Здесь обозначает суммарную кинетическую энергию рассмат-
риваемых материальных точек — 2 |
2 |
2 2, |
|||
|
1 |
1 |
2 |
|
2 |
Æвз 21 |
обозначает бесконечно малую работу силы 21, |
||||
а Æвн 1 |
1 2 2 — бесконечно малую работу внешних |
||||
сил. |
|
|
|
|
|
Из определения энергии взаимодействия (6.16) получаем |
|||||
12 412 412 вз |
вз |
||||
|
|
|
|
|
(6.19) |
Ввиду нашего предположения о потенциальности сил вза- |
|||||
имодействия, работа их от пути не зависит. Поэтому |
работу |
||||

104 Замкнутая система тел [ Гл. 6
вз при удалении тела с расстояния на бесконечность можно совершить, удалив сначала тело по произвольным тра-
екториям на расстояние , а |
затем удалив его из этого |
|
положения на бесконечность, т. е. |
|
|
вз вз вз |
|
|
Подставляя полученный результат в (6.19), получаем |
|
|
12 вз |
Æвз, |
(6.20) |
как следствие, соотношение (6.18) принимает вид
12 Æвн
После перегруппировки слагаемых последнее равенство можно представить как
412 Æвн |
(6.21) |
Если внешние силы отсутствуют, то и Æвн 0. В этом случае из (6.21) следует, что для замкнутой системы
412 0, |
0, |
где - обозначает полную энергию замкнутой системы из двух
материальных точек. В этом случае из (6.21) следует, что полная энергия замкнутой системы двух тел остается при их движении постоянной:
2 |
2 |
|
|
|
|||
- 1 1 |
2 2 |
412 |
|
(6.22) |
|||
|
2 |
|
2 |
||||
|
|
|
|||||
Следует отметить, что утверждение, выраженное формулой (6.22), имеет характер намного более общий, нежели наш вывод, представляющий по сути частный пример. Значение константы (инварианта, интеграла движения) в (6.22) может быть различным, и оно определяется значениями кинетической энергии и энергии взаимодействия в некоторый (например, начальный) момент времени.
Сформулируем теперь закон сохранения энергии для общего случая, когда замкнутая система состоит не из двух, а из произвольного числа ! взаимодействующих материальных точек.
Фомулировка является обобщением формулы (6.22), а именно:
при движении ! материальных точек в замкнутой системе сохраняется ее полная энергия, равная сумме кинетических энергий всех материальных точек и всех попарных потенциальных энергий взаимодействия между ними:
- |
2 |
|
4 , |
(6.23) |
|
2 |
|
|
|
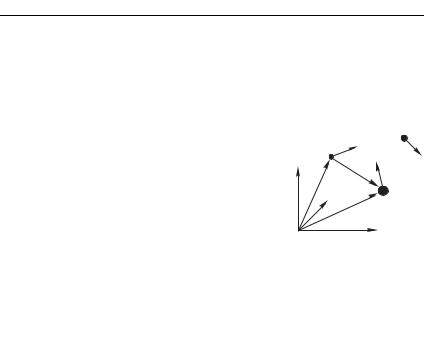
6.3 ] |
|
Потенциальная энергия взаимодействия. |
|
|
|
105 |
||||||
где суммирование по индексам и проводится от 1 до !, и |
||||||||||||
во второй сумме при этом содержатся только слагаемые с & , |
||||||||||||
чтобы не учитывать дважды вклады от энергии взаимодействия |
||||||||||||
каждой из пар материальных точек. Кроме того, для того чтобы |
||||||||||||
сделать запись формулы более компактной, мы ввели обозначе- |
||||||||||||
ния: и 4 4 . Так для замкнутой системы |
||||||||||||
из трех материальных точек (например, |
|
|
|
m2 |
||||||||
тройная звезда) закон сохранения (6.16) |
|
|
|
|||||||||
запишется в виде (рис. 6.5): |
|
|
m1 |
|
v |
|
v2 |
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
2 |
2 |
|
|
|
|
|
z |
r |
- |
v |
3 |
|
|
|
|
|
3 |
|
||||||
1 |
2 |
3 |
|
|
|
|
|
r1 |
|
r |
|
|
|
|
|
|
|
|
|
|
|||||
2 2 |
2 421 431 432 |
|
|
|
1 |
|
||||||
|
y |
|
|
|
m3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
r3 |
|
|
|||
Сколь ни естественно выглядит фор- |
|
x |
|
|||||||||
O |
|
|
|
|||||||||
|
|
|
|
|||||||||
мула (6.23) в качестве обобщения закона |
|
Рис. 6.5 |
|
|||||||||
(6.22), применимость ее ограничена важ- |
|
|
||||||||||
|
|
|
|
|
||||||||
ным дополнительным условием. Мы предположили, что имеет |
||||||||||||
место принцип суперпозиции сил. В случае их потенциальности |
||||||||||||
это означает аддитивность потенциальной энергии: |
|
|
||||||||||
|
|
, 4 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Нарушения этих условий не столь уж и редки (например, взаимодействие нуклонов в ядре не есть сумма их попарных взаимодействий друг с другом). Но в классической механике, пока и поскольку мы не обращаемся к космическим масштабам либо нелинейным свойствам сплошной среды, закон сохранения энергии в форме (6.23) имеет достаточно широкую область применимости. Напомним, что мы показали на примере системы из двух материальных точек, что бесконечно малое изменение их полной энергии равно бесконечно малой работе внешних сил
Æ вн.
Обобщая это на случай произвольного числа материальных точек, мы имеем, следовательно, равенство
Æ вн
Применительно к конечным изменениям энергии оно означает, что изменение полной энергии системы материальных точек равно работе внешних сил. При этом всю потенциальную энер-
гию частиц, составляющих нашу систему, вместе с кинетической
энергией в ц-системе, зачастую удобно интерпретировать как внутреннюю энергию, тем самым представляя систему частиц
вкачестве одного макроскопического тела.
Сучетом теоремы Кёнига (6.13) энергию - системы ! мате-
риальных точек в любой инерциальной системе координат можно

106 Замкнутая система тел [ Гл. 6
записать в виде
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
2 , |
|
- |
|
4 |
2 |
2 |
|
|
|
|
4 |
2 |
, |
|||||||
|
2 |
|
|
2 |
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
где внутренняя энергия , равна |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
, |
2 |
|
|
4 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
Так как — скорости относительно центра масс, то внутренняя энергия системы не зависит от скорости ее движения
как целого и определяется только ее собственными, внутренними свойствами — внутренними степенями свободы. Мы рассмот-
рим данный вопрос на должном уровне в разделе, посвященном термодинамике.
Если система как целое покоится ( 0), то - , — вся энергия системы равна ее внутренней энергии соответственно,
Æвн
6.4. Закон всемирного тяготения
Из астрономических наблюдений известно, по крайней мере, со времен Коперника, что Земля и прочие планеты Солнечной системы обращаются по замкнутым криволинейным орбитам вокруг Солнца. Следовательно, тела эти не свободны, на них постоянно действуют какие-то силы. Идентичность формы орбит дает основание считать, что взаимодействие с Солнцем доминирует. Из третьего закона Ньютона следует, что Земля действует на Солнце с той же силой, с которой Солнце притягивает Землю. Но при рассмотрении законов движения можно работать в системе отсчета, связанной с Солнцем, поскольку при С З приведенная масса (6.3) с хорошей точностью совпадает с массой планеты, а центр масс системы (см. (6.6)) практически совпадает с центром Солнца.
Представим себе, что мы задались целью определить, как зависит от расстояния сила, заставляющая Землю вращаться вокруг Солнца. Для этого можно определить, например, центростремительные ускорения в точке наибольшего удаления Земли от Солнца (в апогее) и в точке наименьшего удаления (в перигее). Во времена Ньютона данные об орбитах планет были уже хорошо известны, т. е. были известны расстояние от Солнца до Земли в апогее а и расстояние в перигее п, а также значение скорости Земли в различных точках ее траектории. Это позволило Ньютону вычислить ускорение Земли в апогее а и в перигееп (в этих точках ускорение Земли, а, следовательно, и сила

6.4 ] |
Закон всемирного тяготения |
107 |
направлены вдоль одной прямой (вдоль большой полуоси), как показано на рис. 6.6). В результате оказалось, что отношение сил, действующих на Землю в этих точках, равно отношению квадратов соответствующих расстояний:
|
2 |
|
|
a |
#п |
|
(6.24) |
|
|||
|
2 |
|
|
п |
#a |
|
|
Естественно предположить, что сила притяжения Земли
к Солнцу, возможно, и при любых их взаимных расположениях |
||||
зависит от расстояния таким же образом. |
|
|
|
|
Такое предположение оказалось в хорошем |
|
Ñ |
Ç |
|
соответствии с законами Кеплера, кото- |
|
|
||
|
|
|
|
|
rï |
rà |
|
|
|
рые будут рассмотрены в следующей гла- |
|
|
||
|
|
|
|
|
ве. Имея в виду эти соображения, Нью- |
|
|
|
|
тон, в конечном счете, высказал гениальную |
|
Рис. 6.6 |
|
|
догадку, что не только между Солнцем и |
|
|
|
|
Землей, а между любыми телами, размерами которых можно пренебречь по сравнению с расстоянием между ними, действует
сила взаимного притяжения, подчиняющаяся закону: сила, с
которой две материальные точки притягивают друг друга, пропорциональна массам этих точек и обратно пропорциональна квадрату расстояния между ними:
5 1 2 |
(6.25) |
|||
|
|
|
||
|
#2 |
|||
|
||||
Здесь 5 — коэффициент пропорциональности, называемый постоянной всемирного тяготения или гравитационной постоянной, числовое значение которой зависит от выбранных единиц измерения. В общепринятой сейчас системе СИ 5 имеет значение
5 6,67 10 11 м3 кг с2
Cформулированный выше закон носит название закона всемирного тяготения, а взаимодействие, о котором идет речь в этом законе, называется гравитационным взаимодействием.
В отличие, скажем, от сил электростатического взаимодействия, гравитационная сила (6.25) всегда есть сила притяжения. В векторной форме она может быть представлена следующим образом:
12 5 |
1 2 12 |
|
(6.26) |
||
2 |
|
|
|||
|
#12 |
#12 |
|
|
|
Выражения (6.25), (6.26) записаны для взаимодействия двух материальных точек, т. е. для тел, размерами которых можно пренебречь из-за того, например, что их размеры намного меньше расстояния между ними (такая, в частности, ситуация имеет место в случае Солнца и Земли). Из них следует, что силу притяжения, действующую со стороны Земли на всякое тело
108 |
|
Замкнутая система тел |
[ Гл. 6 |
||
вблизи ее поверхности, можно с хорошей точностью считать |
|||||
постоянной, не зависящей от удаления тела от земной поверх- |
|||||
ности. Допустим, что тело массы находится от поверхности |
|||||
Земли на высоте , намного меньшей радиуса Земли З , З |
|||||
(напомним, З 6 000 км). Тогда сила, действующая на тело и |
|||||
направленная к центру Земли, равна |
|
||||
5 З |
2 5 2З , |
|
|||
|
|
З |
|
З |
|
где З — масса Земли, а величина 5З З2 |
и есть уско- |
||||
рение свободного |
падения, т. к. она равна тому |
постоянному |
|||
(с точностью до З ) ускорению, с которым движутся к поверх- |
|||||
ности Земли все тела под действием ее притяжения. Учитывая, |
|||||
что З 5,98 1024 кг, З |
6,38 106 м, получаем для ускоре- |
||||
ния свободного падения хорошо известное из школы значение |
|||||
9,8 м/с2, которое с высокой степенью точности подтвержда- |
|||||
ется на опыте. Силу , c которой любое тело притягива- |
|||||
ется к Земле вблизи ее поверхности, называют силой тяжести. |
|||||
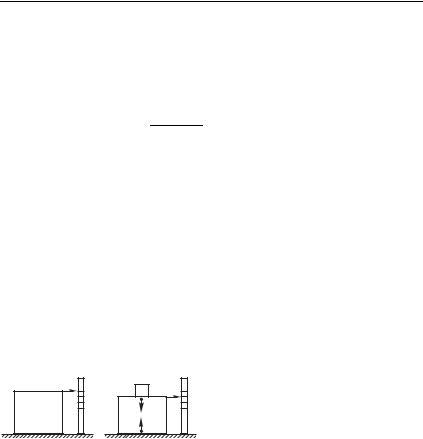
Осталось внести ясность в понятие «вес тела». Чаще всего |
|||||
процесс взвешивания состоит в том, что тело помещают на |
|||||
поверхность определенного устройства — весов, и на шкале этого |
|||||
устройства появляется значение веса, выраженное в единицах |
|||||
измерения силы (например, в килограммах). Таким образом, вес |
|||||
|
|
|
|
тела — это сила, с которой |
|
0 |
|
m |
0 |
взвешиваемое тело действует |
|
1 |
|
|
1 |
на весы. |
|
2 |
|
P |
2 |
|
|
|
|
|
На рис. 6.7 |
схематически |
|
|
|
|
|
||
M |
M |
N |
|
изображены весы в виде твер- |
|
à |
|
á |
|
дого тела, у которого изменение |
|
Рис. 6.7 |
|
|
|
уровня верхней поверхности мо- |
|
|
|
|
жет быть измерено с помощью |
||
|
|
|
|
||
стрелки и соответствующей шкалы, и когда на весах ничего |
|||||
нет, стрелка показывает на нуль (рис. 6.7 а). Когда на весах |
|||||
находится тело массы , то из-за возникающих на поверхно- |
|||||
сти соприкосновения упругих сил эта масса действует на весы |
|||||
с некоторй силой , которая по определению и есть вес тела. |
|||||
Допустим сначала, что весы вместе с телом покоятся отно- |
|||||
сительно Земли, поверхность которой будем рассматривать, как |
|||||
инерциальную систему отсчета. Для вертикальных составляю- |
|||||
щих всех сил, действующих в системе «весы плюс взвешиваемое |
|||||
тело», можно согласно второму закону Ньютона записать сле- |
|||||
дующие два равенства: |
|
|
|
||
! 6 0; ! 0,
где N — сила реакции опоры, на которой расположены весы.
6.4 ] |
Закон всемирного тяготения |
109 |
Отсюда получаем: 6 , т. е. когда весы покоятся, вес тела равен действующей на него силе тяжести.
Теперь рассмотрим случай, когда весы с телом движутся вертикально вверх или вниз с ускорением, равным по модулю :
! 6 ; ! ,
где знак «плюс» справа соответствует движению вверх, а знак «минус» — вниз. Отсюда получаем, что вес тела в этом случае равен: 6 , т. е. при движении весов с телом с ускорением вверх вес тела увеличивается, а при движении вниз — уменьшается. В последнем случае, если (свободное
падение), вес тела становится равным нулю. О такой ситуации говорят, как о состоянии невесомости.
Функциональная зависимость (6.25), (6.26) позволяет с очевидностью отнести гравитационную силу к консервативным. Вычислим потенциальную энергию взаимодействия двух материальных точек с массами 1 и 2, находящихся на расстоянии друг от друга. В соответствии с определением (6.16), получаем из (6.26)
|
|
|
1 2 |
|
, |
412 вз Æвз 12 5 |
|
|
|||
#2 |
# |
||||
|
|
|
|
(6.27) |
|
|
|
|
|
||
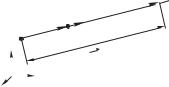
Для удобства вычислений будем удалять тело 2 от тела 1 вдоль соединяющей их прямой линии (рис. 6.8). При этом способе разведения материальных точек вектор бесконечно малого
перемещения тела 2 |
направлен вдоль вектора r, который |
направлен от тела 1 |
к телу 2. Это означает, что . |
Подставляя это соотношение в (6.27), получаем |
|
# |
|
1 5 1 2 |
||||
412 5 1 2 #2 5 1 2 |
|
|
|
|
|
|
# |
# |
|
||||
|
|
|
|
|
|
|
Итак, окончательно, потенциальная |
энергия |
гравитационного |
||||
взаимодействия двух материальных точек с массами 1 и 2, |
||||||||
расположенных на расстоянии 12 |
|
|
|
|
||||
друг от друга, равна |
|
|
|
|
m2 |
|
||
гр |
гр |
|
|
|
m1 |
|
||
1 2 |
|
(6.28) |
r |
|
||||
412 421 5 |
|
|
|
r |
d |
|
||
#12 |
|
8 |
||||||
|
|
|
|
|
|
r |
||
Рассмотрим вопрос о том, какие |
|
|
|
|||||
|
|
0 |
|
|||||
|
|
|
|
|||||
начальные скорости необходимо со- |
|
|
|
|
||||
|
|
|
|
|||||
общить спутнику, чтобы он оставался на замкнутой орбите вблизи
Земли, а также — какие скорости необходимо сообщить телу на Земле, чтобы оно преодолело силу земного притяжения и поки-

110 |
Замкнутая система тел |
[ Гл. 6 |
нуло окрестность Земли, или преодолело притяжение Солнца и покинуло Солнечную систему. Эти скорости получили название «космических скоростей» (их называют, соответственно, первой, второй и третьей космической скоростью).
Определим сначала первую космическую скорость 21. Вблизи поверхности Земли, на высотах З , действующая на тело массы сила притяжения с хорошей точностью равна силе тяжести . Для простоты рассмотрим движение спутника по круговой орбите. В этом случае уравнение движения (второй закон Ньютона) имеет вид
2
"1
З
Пренебрегая по сравнению с |
З |
6, 4 106 |
м, получаем отсюда |
|||
21 |
|
8 103 м/с 8 км/c |
(6.29) |
|||
З |
||||||
Это и есть выражение для первой космической скорости. Именно такую скорость необходимо сообщить телу, чтобы оно стало
спутником Земли.
Вторую космическую скорость можно найти из закона сохранения энергии (6.28). Землю и космический корабль будем рассматривать, как замкнутую систему двух тел, так как влиянием Солнца и других планет можно с хорошей точностью пренебречь. Задача о движении двух взаимодействующих тел сводится к задаче о движении одного тела под действием той же силы, но с приведенной массой 1:
1 З ,
З
где З — масса Земли, — масса корабля. Поскольку масса Земли намного больше, можно положить 1 . Это означает, что влиянием корабля на движение Земли можно пренебречь, т. е. считать Землю неподвижной и рассматривать движение спутника, как движение в постоянном гравитационном силовом поле Земли.
«Освободить» тело от земного притяжения означает дать ему возможность «уйти на бесконечность», где 4гр12 0 Минимальная кинетическая энергия на поверхности Земли, которую ему для этого надо сообщить, отвечает нулевой кинетической энергии в бесконечно удаленной точке:
2 |
|
|
|
|
|
|
"2 |
|
|
5 З |
|
0, |
(6.30) |
2 |
|
З |
|
|
|
|
откуда следует |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
22 25 З |
|
2 З |
(6.31) |
|||
|
|
|
З |
|
|
|
