
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
5.5 ] |
Равновесие и устойчивость |
91 |
5.5. Равновесие и устойчивость
Механика — наука о движении (состояние покоя есть частный случай движения). Наиболее «рафинированное» состояние покоя (или движения с постоянной скоростью) присуще уединенному телу, но этот случай представляет собой идеализированную модель и никогда не реализуется. Наблюдаемое в принципе состояние покоя в системе отсчета, которую мы с необходимой точностью можем считать инерциальной, всегда сводится к одному из двух частных случаев.
1. Силы, действующие на тело, столь малы, и/или характерное время задачи столь коротко, что в пределах точности эксперимента либо точности решения теоретической задачи мы вправе пренебречь ускорением. Если — характерный пространственный масштаб, а — временной, — масштаб действующей силы, а — массы, то мы можем рассматривать тело как покоящееся при условии
2
2. Другой возможный случай, в меньшей степени обусловленный малыми характерными временами, — случай равновесия.
Как было определено в гл. 3, сила есть вектор, а второй закон Ньютона (3.4) — закон векторный. Мы уже отмечали, что это обстоятельство — обобщение огромного массива экспериментальной информации, и что вектор — величина, не просто определяемая модулем и направлением, но и обладающая неко-
торыми специальными свойствами, в частности, она подчиняется принципу суперпозиции. Как следствие, если к телу приложены
две, три и т. д. силы, то ускорение определяется их векторной суммой:
2 |
|
1 |
|
|
|
2 |
|
|
|
||
|
|
||||
|
|
|
|||
Равновесие материальной точки означает, что векторная сумма сил, к ней приложенных, равна нулю:
0 |
(5.29) |
|
|
Если же речь идет о равновесии макроскопического тела, одного условия (5.29) недостаточно. К особенностям движения и равновесия тела конечных размеров мы обратимся в гл. 7, здесь
же ограничимся бесспорным обобщением формулы (5.29): тело пребывает в равновесии, если для любой из материальных то-
чек («физически бесконечно малых объемов»), каковые из этого тела можно выделить, выполнено условие (5.29), включающее как внешние силы, приложенные непосредственно к данному
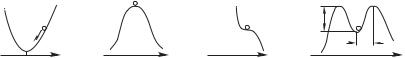
92 |
Работа и энергия |
[ Гл. 5 |
элементу, так и силы взаимодействия с другими элементами данного тела. Разумеется, ни для макроскопического тела, ни даже для такого, которое можно представить как материальную точку, равенство (5.29) никогда не выполняется с совершенной точностью, однако условие малости, позволяющее пренебречь ускорением, налагается уже не на каждую из действующих сил, но лишь на их векторную сумму.
Условия равновесия тел рассматриваются обычно в разделе теоретической механики, именуемом статикой. Мы не будем в нашем курсе изучать ее детально, но остановимся на одном из
важнейших вопросов как в механике, так и вообще в физике — проблеме устойчивости равновесия.
Помимо точности, с которой выполнено само условие равновесия (5.29), существует еще одна причина, способная выводить из равновесия тело или систему тел. Она заключается в хаотических внешних воздействиях, которые невозможно учесть в рамках (5.29). Они могут иметь, например, тепловую природу (поскольку тепловые эффекты обусловлены движением на молекулярном уровне), динамикой Вселенной («свет далекой звезды» вполне может нарушить равновесие идеальной системы), но даже и «замороженная» в мысленном эксперименте Вселенная не будет свободна от квантовых флуктуаций (это предмет следующего тома нашего курса).
Таким образом, равновесие лишь постольку реализуемо, поскольку механическая система устойчива по отношению хотя
бы к достаточно малым внешним воздействиям. Наука об устойчивости сложна и обширна, но мы введем некоторые основные понятия на примере одномерной устойчивости равновесия материальной точки — см. рис. 5.11.
U (x) |
U (x) |
|
|
U (x) |
|
|
U (x) |
|
|
|
|
|
|
U0 |
|
|
|
|
|
|
|
|
|
x0à |
x |
á |
x |
â |
x |
ã |
x |
Рис. 5.11
1.Если при малом нарушении равновесия возникает отклик
ввиде возвращающей силы, материальная точка не может уйти из точки равновесия 0 слишком далеко (рис. 5.11 а). Само воздействие может заключаться либо в перемещении точечной
массы в некоторую точку 0, либо в придании ей некоторой начальной скорости. Она, однако, останется в некоторой окрестности точки 0, если выполнено условие
|
& 0 при & 0; |
' 0 при ' 0, |
|
|
|

5.5 ] Равновесие и устойчивость 93
что сразу следует из (5.24). Иными словами, устойчивому равновесию отвечает минимум потенциальной энергии, что в одномерной задаче эквивалентно условиям:
|
0, |
|
2 |
& 0 |
(5.30) |
||
|
|
|
|||||
|
|
2 |
|||||
0 |
|
||||||
|
|
0 |
|
||||
|
|
|
|
|
|
||
Как мы уже знаем из гл. 4, эффект возвращающей силы сводится к некоторым колебаниям вблизи положения равновесия. Если функцию можно при малых отклонениях линеаризовать, то это будут просто гармонические колебания — например, (4.18). При учете трения либо иных механизмов диссипации (вязкость, излучение акустических или электромагнитных волн, химические реакции и пр.) колебания должны быть затухающими, и частица со временем — по крайней мере, асимптотически —
возвращается в положение равновесия. |
|
|
2. Предположим, что функция , |
не |
имеет минимума |
в точке равновесия (рис. 5.11 б, в). Тогда |
нет |
и устойчивости. |
В случае максимума , — рис. 5.11 б — смещение частицы в любую сторону приводит к тому, что и ускорение оказывается направлено в сторону смещения, так что вернуться в точку 0 частица не может. В ситуации, изображенной на рис. 5.11 в, частица может вернуться в 0, если либо смещение, либо начальная скорость были отрицательны — но вернется она только один раз, а далее воспроизводится сценарий, соответствующий рис. 5.11 б. Иногда выделяют особо случай безразличного равновесия, когда 0, т. е. , Но он отличается от вариантов рис. 5.11 б, в лишь функционально, возвращения частицы в положение равновесия не происходит. Истинное устойчивое равновесие может быть обусловлено лишь минимумом потенциальной энергии (5.30).
В современной механике и физике различают линейную и нелинейную устойчивость. Проблема иллюстрируется рис. 5.11 г.
При малых отклонениях от равновесия частица в него возвращается. Но если она выходит за границу 0 & или ей сообщают кинетическую энергию, превышающую ,0, частица в равновесие уже не вернется. Величины ,0 и определяют порог нелинейной неустойчивости. Легко сообразить, что при достаточной амплитуде воздействия любая система оказывается нелинейно неустойчивой — хотя бы на уровне разрушения. Но это уже вовсе не обязательно связано со случайными самопроизвольными отклонениями от равновесия.
Все примеры данного параграфа достаточно естественным образом переносятся и на неодномерный случай, и на случай макроскопических тел, а равно и сложных систем, когда, быть может, не все параметры системы 0 , определяющие устойчи-
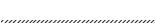
94 |
Работа и энергия |
[ Гл. 5 |
вость, сводятся к пространственным координатам. Правильный язык для такого «перевода» — формализм потенциальной энергии, а главная проблема — отыскание функции , 01, 02, .
Вопросы и задачи
1.Что такое потенциальная энергия материальной точки?
2.Что такое принцип суперпозиции сил?
3.Может ли потенциальная энергия быть отрицательной?
4.Почему затухают колебания пружины?
5.Почему нагреваются трущиеся поверхности?
6.Имеет ли значение знак потенциальной энергии для устойчивости равновесия?
7.Тело, размерами которого можно пренебречь, начинает скользить с нулевой начальной скоростью по гладкой поверхности, образованной четвертью сферической поверхности радиуса из ее верхней точки. Достигнув нижней точки, тело продолжает двигаться по шероховатой поверхности, где коэффициент трения скольжения равен . Чему равно расстояние , которое тело пройдет по шероховатой поверхности до остановки? Переход от криволинейной поверхности к плоской горизонтали считать сглаженным так, что удара в этой
точке не происходит.
Ответ: .
8. Какова минимальная работа, которую надо затратить, чтобы втащить волоком тело массы на горку длины и высоты ? Коэффициент трения
равен .
Ответ:
9. Математический маятник (груз малых размеров на легком подвесе длины ) находится в положении равновесия. Определите, какую скоростьнадо сообщить грузу, чтобы он мог совершить полный оборот, для двух случаев: груз подвешен а) на жестком стержне и б) на нити.
Ответ: а) 2 4 ; б) 2 5 .
Ук а з а н и е . Во втором случае скорость в верхней точке должна быть достаточно велика, чтобы сила тяжести не превышала необходимой центростремительной силы.
10. На столе лежит доска массы 1 кг, а на доске — груз массы2 кг. Какую силу надо приложить к доске, чтобы она выскользнула
из-под груза? Коэффициент трения между грузом и доской равен 1 0,25, а |
||||||
между доской и столом — 2 0,5 |
||||||
|
Р е ш е н и е . Сумма сил, действующих на доску, равна 1 1 |
|||||
2 , на груз — 2 |
2 . Чтобы доска могла выскользнуть |
|||||
|
|
|
|
|
|
из-под груза, ее ускорение должно быть |
|
|
|
|
|
|
больше ускорения груза, т. е. 1 2 . |
|
|
M |
|
|
||
|
|
|
Отсюда получаем 1 2 |
|||
|
k1 |
|
k2 |
|
22,5 Н. |
|
|
|
|
|
|||
|
|
m |
|
|
11. Тело массы колеблется без тре- |
|
|
|
|
|
|
|
ния, двигаясь по дну коробки массы , ле- |
|
|
|
|
|
|
жащей на горизонтальной поверхности стола, |
|
|
Рис. 5.12 |
под действием двух пружин жесткости 1 и 2 |
|||
|
|
(см. рис. 5.12). Коэффициент трения коробки |
||||
|
|
|
|
|
|
|
о стол равен . При какой амплитуде колебаний тела коробка начнет |
||||||
двигаться по поверхности стола? |
|
|||||
|
Ответ: 1 2 |
|||||

Г л а в а 6
ЗАМКНУТАЯ СИСТЕМА ТЕЛ. ЭНЕРГИЯ
ВЗАИМОДЕЙСТВИЯ И ВНУТРЕННЯЯ ЭНЕРГИЯ
6.1. Особенности движения замкнутой системы из двух взаимодействующих материальных точек.
Приведенная масса
До сих пор мы изучали наиболее простые движения — движения, при которых размеры тела не играют роли, т. е. использовали приближение (модель) материальной точки. При этом мы рассматривали лишь случай, когда сила, действующая на материальную точку, известна (движение в поле тяжести, гармонические колебания, закон сохранения энергии при движении в постоянном силовом поле).
Теперь, руководствуясь правилом «от простого — к сложному», мы сделаем следующий шаг — рассмотрим особенности движения нескольких взаимодействующих материальных точек. В этом случае действующую на каждую из них силу со стороны остальных тел нельзя уже считать заданной величиной, так как она зависит от меняющегося положения этих остальных тел, траектории движения которых заранее не известны. Так, например, в одном узле сложного механизма часто оказываются соединенными несколько деталей, оказывающих воздействие друг на друга и совершающих друг относительно друга сложные движения. Один из простейших примеров такого взаимодействия изображен на рис. 6.1: две материальные точки с массами 1 и 2
соединены пружиной и совершают по |
|
|
горизонтальной плоскости колебания |
|
|
друг относительно друга. Ситуация |
|
|
здесь отличается от той, которая рас- |
|
|
сматривалась в гл. 4, где мы изучали |
|
|
гармонические колебания одного тела, |
Рис. 6.1 |
|
соединенного пружиной со стенкой. |
||
|
||
Изучение движения нескольких взаимодействующих тел мы |
||
начнем с простейшего случая — движения всего двух материальных точек, при движении которых можно пренебречь всеми действующими на них силами, кроме сил, с которыми они действуют друг на друга. Другими словами, эти две материальные точки образуют замкнутую систему тел. Массы этих тел обозначим

96 |
|
|
Замкнутая система тел |
[ Гл. 6 |
||||||
через 1 и 2 (рис. 6.2). Силу, действующую на тело 1 со |
||||||||||
стороны тела |
2, обозначим 12. Она, в соответствии с третьим |
|||||||||
законом Ньютона, равна по величине и противоположна по на- |
||||||||||
z |
|
|
|
|
правлению силе 21, действующей на |
|||||
|
|
|
|
тело 2 со стороны тела 1. Положение |
||||||
|
|
F |
|
|
||||||
|
m1 |
|
|
наших тел в некоторой произвольно |
||||||
|
12 |
|
|
|||||||
|
|
|
|
|
выбранной |
инерциальной |
системе от- |
|||
|
) |
r( |
|
|
счета определяется в момент времени |
|||||
|
t |
|
|
|||||||
|
( |
t |
|
|
|
|
|
|
|
|
r |
1 |
) |
F |
|
соответствующими радиусами-вектора- |
|||||
|
21 |
|
||||||||
y |
|
|
||||||||
|
|
m |
|
ми этих тел 1 и 2 . |
|
|||||
|
|
) |
|
|
||||||
|
|
(t |
2 |
|
|
|
Перейдем к изучению особенностей |
|||
|
|
r2 |
x |
|
|
|
||||
O |
|
|
|
движения этих двух тел с помощью |
||||||
|
|
|
|
|||||||
|
|
Рис. 6.2 |
|
|
второго закона Ньютона. Записав этот |
|||||
|
|
|
|
закон для каждой из материальных то- |
||||||
|
|
|
|
|
||||||
чек, получим следующую систему уравнений относительно инте- |
||||||||||
ресующих нас радиусов-векторов 1 и 2: |
|
|||||||||
|
|
|
|
1 |
2 1 |
|
, |
|
||
|
|
|
|
2 |
12 |
2 |
1 |
(6.1) |
||
|
|
|
|
|
2 2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
2 21 2 1 |
|
||||
Прежде всего мы рассмотрим задачу об относительном движении двух тел. На языке математики относительное дви-
жение определяется зависимостью от времени радиуса-вектора2 1, соединяющего две рассматриваемые материальные точки. Уравнение для легко получить из нашей системы двух уравнений (6.1) следующим способом. Поделим обе части первого из уравнений на 1, а обе части второго уравнения — на 2. После этого вычтем из левой и правой частей второго уравнения левую и правую части первого соответственно. В результате получаем
2 2 1 |
|
1 |
|
1 |
21 2 1 |
, |
2 |
2 |
1 |
||||
где мы учли, что 12 21. Последнее уравнение можно окончательно записать в виде
1 |
2 |
21 , |
(6.2) |
2 |
|||
|
|
|
|
где буквой 1 мы обозначили величину, равную
1 1 2 |
(6.3) |
|
|
1 2 |
|
|
|
|
и называемую приведенной массой.
Уравнение (6.2) отражает замечательное свойство задачи о
движении двух взаимодействующих материальных точек: задача об относительном движении двух материальных точек
6.1 ] |
Система из двух материальных точек. Приведенная масса |
97 |
в замкнутой системе сводится к задаче о движении одной материальной точки с приведенной массой под влиянием той же самой силы взаимодействия.
Одним из примеров замкнутой системы двух тел является система «Солнце–Земля», если пренебречь влиянием других тел Солнечной системы, что в действительности можно сделать с хорошей точностью. Для вычисления траектории движения Земли относительно Солнца нет необходимости решать систему из двух уравнений (6.1), т. е. находить сначала 1 и 2 (траектории Солнца и Земли в некоторой инерциальной системе координат) и только после этого уже определять 2 1 (траекторию относительного движения). Вместо этого можно сразу найти траекторию относительного движения, решая всего одно уравнение (6.2), что и сделал в свое время Ньютон, блестяще подтвердив расчетами знаменитые опытные законы Кеплера. Правда в этом случае в уравнение относительного движения войдет приведенная масса, которая для системы «Солнце–Земля» равна
1 С З |
З |
|
||
|
С З |
|
1 З С |
|
Масса Солнца примерно в двести тысяч раз больше массы Земли. Поэтому во многих практически важных задачах отношением масс в знаменателе последней формулы можно с хорошей точностью пренебречь, и считать, что приведенная масса для системы «Солнце–Земля» совпадает с массой Земли.
Что касается задачи об относительном движении двух тел, соединенных невесомой пружиной (рис. 6.1), то в этом случае на тела помимо упругой силы, играющей здесь роль силы 12, действуют еще сила тяжести и реакция опоры. Эти силы, однако, уравновешивают друг друга и не оказывают влияния на движение тел. Поэтому в отсутствие сил трения движение тел по горизонтальной поверхности подчиняется законам движения замкнутой системы, и, следовательно, задача об их относительном движении сводится к рассмотренной в гл. 4 задаче о движении одного тела, но с приведенной массой. Например, для случая колебаний двух тел с одинаковой массой их приведенная масса 1, в соответствии с (6.3), равна 2. Тогда для вычисления, скажем, частоты относительных колебаний таких двух тел можно воспользоваться уже известной нам формулой (4.18) для частоты колебаний одного тела, соединенного пружиной со
стенкой, а именно, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
||||
! |
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||
|
|
|||||||||||
т. е. частота колебаний в |
рассматриваемом случае в |
2 |
раз |
|||||||||
больше, чем в случае колебаний одного тела.
4 Основы физики. Т. I

98 |
Замкнутая система тел |
[ Гл. 6 |
6.2. Центр масс системы материальных точек
Если бы мы не вычитали, а складывали уравнения (6.1), у нас получился бы просто закон сохранения импульса
1 1 2 2 0
Его можно переписать чисто формально как закон постоянства во времени некоторой скорости :
1 1 |
2 2 |
|
(6.4) |
|
|
1 |
|
||
2 |
|
|||
|
|
|||
Перейдем в систему отсчета, движущуюся со скоростью (6.4). Скорости частиц 1 и 2 при этом преобразуются следующим образом:
|
|
1 |
|
1 |
2 |
; |
|
|
1 |
2 |
1 |
, (6.5) |
|
|
|
|
|
||||||||
1 |
|
|
2 |
|
2 |
2 |
2 |
1 |
2 |
|||
|
|
|
1 |
|
|
|||||||
т. е. в новой системе отсчета они выражаются через скорость относительного движения. Свяжем скорость с радиусомвектором некоторой точки :
|
|
|
; |
|
1 1 |
2 2 |
(6.6) |
|
|
|
|||||
|
|
|
1 |
2 |
|
||
Отметим, что определение (6.6) совпадает с известным из школьного курса физики понятием центра тяжести. Для доказательства перенесем начало координат в точку . Тогда, совершенно аналогично (6.5), получим
1 |
2 |
1 2 |
; |
|
2 1 |
2 1 |
|
|
|
||||||
1 |
|
1 2 |
|
2 |
|
1 2 |
|
Таким образом, 1 1 2 2 (центр тяжести определяется равенством произведений массы на «плечо»). Но определения (6.4) и (6.6) более корректны и более универсальны, поскольку без каких-либо проблем обобщаются на любое число материальных точек, а следовательно, и на макроскопические тела.
Точку % в механике — и вообще в физике — принято называть
центром масс или центром инерции системы материальных точек.
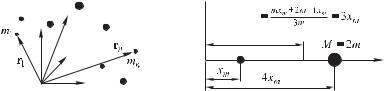
Пусть в некоторой инерциальной системе координат положения взаимодействующих материальных точек с массами 1,
2, задаются в каждый момент времени посредством
радиусов-векторов 1 , 2 , (рис. 6.3 а). Тогда центром масс рассматриваемой системы материальных точек
называется такая точка, радиус-вектор которой выражается через радиусы-векторы 1, 2, материальных точек по формуле
|
1 1 2 2 |
|
(6.7) |
|
1 2 |
|
6.2 ] |
Центр масс системы материальных точек |
99 |
Подчеркнем, что в общем случае положение центра масс не совпадает с положением какой-либо из материальных точек системы (рис. 6.3 б), хотя иногда такое может и случиться.
|
. |
|
xC |
|
RC |
z |
xC |
y |
m |
|
x |
|
x |
O |
|
à |
á |
|
Рис. 6.3 |
Продифференцируем по времени левую и правую части равенства (6.7). Производная радиуса-вектора по времени есть по определению скорость, так что в результате мы получаем
|
1 |
1 1 2 2 , |
|
||
|
1 2 |
|
(6.8) где — скорость центра масс; 1, 2, — скорости материальных точек. Величина 1 1 в (6.8) — импульс первой материальной точки, 2 2 — импульс второй точки и т. д. Таким образом, в фигурных скобках выражения (6.8) стоит сумма импульсов рассматриваемой системы материальных точек, т. е. импульс всей системы. Следовательно, равенство (6.8) можно переписать в виде
1 2 |
(6.9) |
В системе отсчета, где центр масс покоится, 0 Если нас не интересует относительное движение материаль-
ных точек, а интересует движение системы как целого, то тогда всю систему можно рассматривать как одну материальную точку, движущуюся со скоростью и обладающую импульсом P. Вспомним, что масса материальной точки есть, по определению, коэффициент пропорциональности между импульсом и скоростью. Поэтому стоящий в равенстве (6.9) коэффициент пропорциональности, заключенный в фигурные скобки, есть масса
рассматриваемой системы: |
|
1 2 , |
(6.10) |
т. е. масса системы материальных точек равняется сумме масс этих точек. Соотношение (6.10), согласно которому масса сложного тела равна сумме масс его частей, кажется нам привычным и очевидным. Однако, как мы еще убедимся, в релятивистской механике (т. е. в более общем случае) ситуация будет
4*

100 |
Замкнутая система тел |
[ Гл. 6 |
совершенно иной. В предельном случае ньютоновой механики
равенство (6.10) представляет собой частный случай определенного физического закона — закона сохранения массы.
В отсутствие внешних сил, т. е. для замкнутой системы, сумма импульсов всех тел системы не зависит от времени; тогда из (6.9) следует важное свойство движения центра масс замкнутой системы материальных точек:
,
т. е. центр масс замкнутой системы материальных точек неподвижен или движется равномерно и прямолинейно, хотя
каждая из материальных точек может совершать сложное движение. Приведенное выше утверждение называют иногда теоремой о движении центра масс.
Мы сейчас докажем следующее важное свойство кинетической энергии: кинетическая энергия системы материальных точек равна сумме кинетической энергии всей массы системы, мысленно сосредоточенной в ее центре масс и движущейся вместе с ним, и кинетической энергии той же системы в ее относительном движении по отношению к системе отсчета, движущейся вместе с центром масс:
|
1 |
|
2 1 |
|
|
2 |
|
|
||
|
2 |
2 |
2 |
|
, |
(6.11) |
||||
2 |
|
2 |
|
2 |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
где 1 2 , |
|
— скорость |
|
центра масс |
||||||
в исходной системе отсчета, |
— скорость |
-ой материальной |
||||||||
точки относительно системы отсчета, движущейся вместе с точкой %. Такую систему обычно называют «системой центра масс», «системой центра инерции» или просто «ц-системой». (Систему
|
|
|
|
|
|
|
|
|
отсчета, в которой поставлена задача, |
|
|
|
|
|
|
|
|
|
если эта система не совпадает с ц-сис- |
|
|
|
z |
|
|
mi |
|
|
темой, принято называть лабораторной |
|
|
|
|
|
|
|
|
системой отсчета или л-системой). |
|
|
|
|
|
ri |
|
|
|
||
|
|
|
|
y |
|
x |
Для доказательства получим вна- |
||
|
|
|
O |
|
|
|
чале более общее соотношение, связы- |
||
|
|
|
|
|
|
|
|
||
z |
|
|
|
|
|
|
|
|
вающее кинетическую энергию в двух |
|
|
|
|
|
|
|
|||
|
|
R |
|
Ri |
|
|
|
системах отсчета (рис. 6.4). Для коор- |
|
|
|
|
y |
|
|
|
динат и скоростей точек в старой си- |
||
|
|
|
|
x |
|
|
|
стеме , и в новой системе , |
|
O |
|
|
|
|
|
|
запишем преобразования Галилея: |
||
|
|
|
|
|
|
|
|
||
|
|
|
Рис. 6.4 |
|
|
|
; , |
||
где R — радиус-вектор перехода из старой системы в новую, а V — соответственно скорость движения новой системы относительно старой. Тогда кинетическую энергию в старой системе
