
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf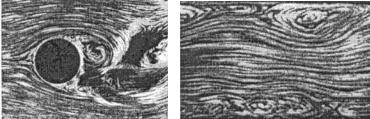
8.6 ] |
Турбулентность |
161 |
8.6. Турбулентность
Формула Пуазейля применима только для ламинарных течений жидкости. Ламинарным называется такое течение, когда
жидкие частицы движутся вдоль устойчивых траекторий. При достаточно больших скоростях ламинарное течение становится неустойчивым, хаотичным и переходит в так называемое турбулентное течение. При этом основные уравнения гидродинамики остаются в силе, но большинство результатов настоящей главы должно быть подвергнуто ревизии.
Характер турбулентных движений может быть весьма раз-
личным в зависимости от внешних условий. Из повседневного опыта нам более всего знакомо явление гидродинамической турбулентности несжимаемой жидкости — представление о
таком режиме дает турбулентная струя, вытекающая из крана. Реализуется данное состояние жидкости в случае перепада скоростей течения, много меньшего скорости звука. Для него характерно образование множественных вихрей (М. В. Ломоносов подразделял течения жидкости на «покойные» и «коловратные»). На рис. 8.16 а схематически изображено образование вихрей при обтекании несжимаемой жидкостью шара, а на рис. 8.16 б — при течении в прямой трубе.
à |
á |
Рис. 8.16
Следует особо обратить внимание на то, что во всех оценках, относящихся к турбулентному состоянию, фигурирует не скорость течения как таковая, а именно перепад скоростей . Действительно, если некоторое течение происходит с постоянной всюду скоростью v, мы можем, переходя в движущуюся систему отсчета, сделать эту скорость как угодно малой или большой, так что подлинная «индивидуальность» течения может быть отражена лишь величиной .
Хотя детальное рассмотрение физики турбулентных состояний далеко выходит за рамки нашего курса, мы все же можем кое-что сказать о переходе от ламинарного («покойного») к тур-
булентному («коловратному») течению. Принципиальным моментом здесь будет использование методов подобия и размерно-
6 Основы физики. Т. I

162 |
Элементы механики сплошных сред |
[ Гл. 8 |
сти. Дело в том, что размерность физических величин — не только один из важных методов контроля правильности ответов, но и метод получения новых результатов в физике вообще и в механике, в частности, хотя возможности его ограничены и предсказательная сила не абсолютна (чему последующее рассмотрение будет хорошим примером).
Попробуем проанализировать физические предпосылки перехода к турбулентному течению, представленному на рис. 8.16. Пока и поскольку течение остается ламинарным, у него сохраняется характерный пространственный масштаб (радиус шара на рис. 8.16 а либо диаметр трубы на рис. 8.16 б). Турбулизация течения приводит к измельчению масштаба, а значит, и к росту пространственных производных от скорости, чему, как можно усмотреть из формул (8.27), (8.28), противодействуют эффекты,
обусловленные вязкостью. Таким образом, чем больше вязкость жидкости, тем более затруднен переход в турбулентное
состояние. Еще более очевидным представляется следующее утверждение: чем больше перепад скоростей, тем легче переход из ламинарного режима в турбулентный — скажем,
в предельном случае пространственно-однородного течения турбулентности просто не может быть, поскольку оно эквивалентно состоянию покоя.
Как уже указывалось выше, размерность вязкости составляет
@
Составим безразмерную комбинацию
Re
4
Подставляя в это выражение значения характерных параметров:
33, , |
, |
получим величину |
|
|
|
Re % , |
(8.34) |
4 |
|
которую принято называть числом Рейнольдса (по имени английского физика О. Рейнольдса (1842–1912)). Число Рейнольдса можно переписать в виде
2 3
Re % ,
42
откуда следует, что оно характеризует отношение кинетической энергии движущейся жидкости 32 3 2 к потере этой энергии, равной работе сил вязкости на характерной длине ,@2. Помимо вязкости @, жидкость характеризуется еще и плотностью 3, а течение как таковое — пространственным
8.7 ] |
Вопросы и задачи |
163 |
масштабом и характерным перепадом скоростей . (Применительно к ситуации рис. 8.16 это просто скорость по порядку величины, так как вблизи неподвижных стенок скорость должна обращаться в нуль). Изложенные выше рассуждения позволяют заключить, что чем больше величина Re, тем благоприятнее ситуация для турбулентного течения, и напротив, для течений с малыми числами Рейнольдса должен, по-видимому, реализоваться ламинарный режим.
Данные эксперимента находятся с этими соображениями
в полном согласии. Оказывается, действительно существует критическое число Рейнольдса, при превышении которого происхо-
дит переход из ламинарного режима в турбулентный. Но сама величина Reкр, как показывает опыт, не универсальна — она зависит от геометрии системы. Например, в случае течения по трубе (рис. 8.16 б) Reкр 2 103, тогда как при вращении цилиндра в газе переход в турбулентный режим происходит при Reкр 50. В этом и состоит некоторая слабость чисто размерностной оценки.
Но у нее есть и очень сильная сторона. Сами по себе величины 3, , , @ могут меняться в очень широком диапазоне; скажем труба может быть капилляром, а может быть аэродинамической трубой диаметром в десятки метров — ответ, тем не менее, будет универсальным и опираться он будет всего
лишь на одну безразмерную комбинацию — число Рейнольдса. Такие зависимости называются в физике законами подобия, а
переход на их основании от одних экспериментальных ситуаций к другим принято именовать скэйлингом. Таким образом, если
для некоторого физического явления известен закон подобия, мы можем ставить эксперименты в малом масштабе, так чтобы они были более дешевыми или, например, более безопасными, а затем проводить скэйлинг для получения ответа в интересующем нас масштабе. Поэтому методы подобия и размерности занимают достаточно почетное место в арсенале современной физики.
Вопросы и задачи
1.Каким числом констант описываются упругие свойства изотропного вещества?
2.Можно ли ввести модуль сдвига для стекла?
3.Из каких свойств жидкостей и газов следует закон Паскаля?
4.Что такое вязкость?
5.Допустимо ли использовать уравнение Бернулли для вязкой жидкости?
6.Оценить давление в центре Земли, полагая плотность вещества посто-
янной и равной % 5,5 103 г/см3. Радиус Земли 6 400 км.
Решение. Поскольку объемная плотность силы тяжести, в отличие от простых «настольных» задач, зависит от расстояния до центра Земли, уравнение
6*

164 |
Элементы механики сплошных сред |
[ Гл. 8 |
равновесия, с учетом (8.19), следует в данном случае использовать в виде:
% # 0, |
где # |
|
, |
# |
4 |
#3% |
|
|
|||||
|
2 |
|
3 |
|
||
Мы учли то обстоятельство, что в случае сферической симметрии все ве-
личины зависят только от #; что сила тяжести направлена к центру Земли, т. е. против r — отсюда и знак « », и, наконец, что внешние слои Земли с радиусами, б´ольшими #, вклада в силу притяжения не дают (см. гл. 6). Окончательно,
|
|
|
4 |
,%2# |
2 |
,%2#2 |
2 |
,%2 2 #2 , |
|
|
|
3 |
3 |
3 |
|||||
если учесть, что на поверхности Земли, |
т. е. при # , 0. Подстав- |
||||||||
ляя % 5,5 103 кг/м3, 6,4 106 м, |
получаем 0 2,6 |
||||||||
1011 Па 2,6 106 атм. Б´ольшая точность в оценках бессмысленна, хотя бы по той причине, что плотность вещества не может быть инвариантной при таком перепаде давлений.
7. Определите отношение энергий деформации стального и пластмассового цилиндров одинаковых размеров для двух случаев: 1) цилиндры поставлены рядом друг с другом и сжаты параллельными плоскостями; 2) цилиндры поставлены друг на друга и также сжаты плоскостями. Модуль Юнга для
стали равен *1 2 105 Н/мм2 |
, для пластмассы — *2 102 Н/мм2. |
|
Ответ: 1) 1 2 *1*2 |
2 103; 2) 1 2 *2*1 5 10 4 |
|
8. В вертикально стоящий цилиндрический сосуд налита идеальная жид- |
||
кость до уровня |
(относительно дна сосуда). Площадь дна сосуда равна |
|
(. Определить время , за которое вся жидкость выльется из сосуда, если в дне сосуда сделано малое отверстие площади -. Считать режим течения несжимаемым.
Решение. Движение не стационарно — скорость истечения меняется, и верхняя граница жидкости движется. Уравнением Бернулли, полученным для стационарного течения, можно пользоваться, если эти изменения происходят медленно, как в случае - (. Обозначим высоту поверхности жидкости относительно дна сосуда в момент через , скорость жидкости на этой поверхности (скорость движения частиц, находящихся на границе) — через1 , скорость жидкости в отверстии — через 2. Учитывая, что давление на верхней поверхности жидкости и на поверхности вытекающей струи примерно одинаково (равно атмосферному) и что в силу несжимаемости
жидкости 1( 2-, получаем из уравнения |
Бернулли, рассматривая всю |
||||||||
2 |
2 |
2 . Учитывая, что - (, |
|||||||
жидкость как единую трубку тока, 2 1 |
|||||||||
находим |
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|||||
|
|
|
|||||||
После интегрирования отсюда получаем |
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||
Полагая здесь 0, определяем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2! |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
9. Из неплотно закрытого крана вытекает в единицу времени количество воды 5 1 см3/с. Вода попадает в сосуд и затем вытекает из него по горизонтальной трубке длины 20 см. Со временем в сосуде устанавливается уровень воды на 5 см выше уровня трубки. Определите диаметр трубки. Вязкость
воды 4 10 3 Па с.
Ответ: 2 8 4 % 5 1 4 2 мм.
Г л а в а 9
ЗАКОНЫ МЕХАНИКИ В НЕИНЕРЦИАЛЬНЫХ СИСТЕМАХ ОТСЧЕТА
9.1. Принцип относительности Галилея
Как меняются законы движения при переходе из одной системы отсчета в другую? Другими словами, меняется ли при этом (и как) основной закон механики — второй закон Ньютона —
Этот вопрос имеет очень важное значение, так как наблюдать за движением тел и использовать законы механики на практике приходится не в одной какой-то, раз и навсегда выбранной системе отсчета, а в различных системах, по-разному движущихся друг относительно друга. Особое значение придает данной проблеме то обстоятельство, что инерциальная система отсчета, в которой мы до настоящего времени формулировали законы механики, есть физическая идеализация, тогда как в природе мы всегда имеем дело с неинерциальными системами.
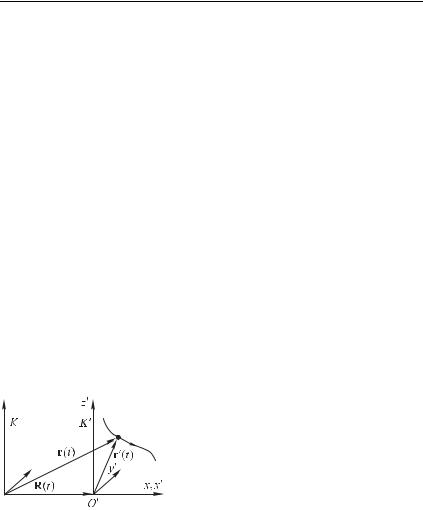
Рассмотрим случай, когда обе системы отсчета — исходная и движущаяся относительно нее — являются инерциальными системами. Допустим, что система отсчета инерциальна, а система движется относительно первой поступательно с постоянной скоростью (рис. 9.1). Для простоты можно принять, что координатные оси ,
, соответственно параллельны |
|
|
y |
|
|
m |
|
|
|
|
|
||||
|
|
|
|
|
|||
осям , , и что в начальный мо- |
|
|
|
|
|
|
|
мент времени 0 начало сов- |
|
|
|
r |
|
|
|
мещается с началом . Будем также |
|
|
|
|
|
|
|
считать, что скорость параллельна |
|
|
O |
|
|
|
|
оси . При этих условиях ось все |
|
K |
|
|
|
|
|
|
|
|
|
V |
|||
время будет совпадать с осью . Та- |
z |
|
|
|
|
||
|
|
|
|
|
|
||
кие упрощения в постановке задачи |
Рис. 9.1 |
|
не лишают ее общности, так как пе- |
||
|
реход к общим формулам может быть совершен дополнительным поворотом координатных осей и переносом начала координат. Радиус-вектор некоторой материальной точки в исходной системе отсчета в момент времени обозначим через , а ради- ус-вектор той же материальной точки в тот же момент времени

166 Законы механики в неинерциальных системах отсчета [ Гл. 9
в движущейся системе обозначим через . Тогда координаты и время в системах и будут связаны друг с другом соотно-
шениями |
, |
, |
(9.1) |
или в проекциях на оси |
|
|
|
2 , , |
, |
|
|
Мы уже обсуждали эти соотношения в гл. 2. Напомним, что они называются преобразованиями Галилея. Мы добавили к формулам преобразования координат дополнительную формулу , выражающую предположение Ньютона о том, что время является абсолютным, то есть текущим одинаково в любых системах отсчета.
С точки зрения нашего повседневного житейского опыта, преобразования Галилея кажутся очевидными. В самом деле, они фактически основаны на двух предположениях. Во-первых, предполагается, что в разных системах отсчета остаются неизменными длины одних и тех же твердых стержней, которые используются для измерения пространственных размеров и координат различных тел. Кроме того, преобразования Галилея предполагают также, что, например, показания часов у двух человек не станут различаться только из-за того, что один из них начнет идти быстрее другого, и это тоже, казалось бы, не вызывает сомнения. Но всегда ли здравый смысл достаточен для доказательства истины? Об этом пойдет речь в следующей главе, а сейчас поговорим о том, что означают преобразования Галилея с точки зрения формулировки законов механики в разных инерциальных системах. Различаются ли законы движения для наблюдателей в разных системах?
Дифференцируя соотношение (9.1) по времени , получим
|
|
|
|
|
|
, |
|
|
|
||
|
|
|
|
или |
(9.2) |
||
, |
|||
где — скорость материальной точки в системе , а |
— |
||
в системе . Эта формула выражает известное уже нам правило сложения скоростей в механике Ньютона.
Дифференцируя второй раз , получим (с учетом постоян-
ства |
|
|
|
|
, |
||
|
|
|
|
или |
|
(9.3) |
|
|
|||
Таким образом, ускорение инвариантно относительно преобразований Галилея.
9.2 ] |
Законы механики в неинерциальных системах отсчета |
167 |
С правилом сложения скоростей и с равенством (9.3) мы познакомились впервые в гл. 2. Поставим теперь вопрос: а как меняется сила при переходе из одной инерциальной системы в другую? Сила зависит от разности координат взаимодействующих материальных точек (для электромагнитных сил — еще
иот разности их скоростей). Поэтому, в соответствии с (9.1)
и(9.2), сила не меняется при переходе от одной системы отсчета к другой: . Такие соображения, сколь бы они не казались естественными, ни в коей мере не являются доказательством — они, например, должны быть пересмотрены в рамках релятивистской механики. Иначе говоря, сила инвариантна лишь относительно преобразований Галилея. Это утверждение должно рассматриваться как опытный факт. Так как и ускорение инвариантно, а масса материальной точки предполагается величиной постоянной, не зависящей от ее положения и скорости, то второй закон Ньютона в «штрихованной» системе принимает вид
Это уравнение в «штрихованной» системе отсчета имеет точ-
но такой же вид, что и в «нештрихованной» системе . Таким образом, уравнения механики Ньютона инвариантны относительно преобразований Галилея. Это утверждение составляет содержание принципа относительности Галилея.
Принцип относительности Галилея провозглашает полное равноправие всех инерциальных систем отсчета и его можно
сформулировать также в виде следующего утверждения: никакими механическими опытами, проведенными в пределах только данной системы отсчета, нельзя установить, находится ли она в состоянии покоя или в состоянии равномерного прямолинейного движения. Находясь, например, в вагоне поезда,
движущегося без толчков прямолинейно и равномерно, мы, не выглянув в окно, не сможем определить, движется вагон или покоится. Свободное падение тел, движение брошенных нами предметов и все другие механические процессы будут в этом случае происходить так же, как и в случае, если бы вагон был неподвижен.
9.2. Законы механики в неинерциальных системах отсчета. Силы инерции
Рассмотрим теперь вопрос о том, как формулируются законы механики в неинерциальных системах отсчета. Вопрос этот имеет важное практическое значение: система отсчета, связанная с поверхностью Земли, не является инерциальной — например, в системе отсчета, связанной с Солнцем, точки на поверхно-
168 |
Законы механики в неинерциальных системах отсчета |
[ Гл. 9 |
||||||
сти Земли испытывают центростремительное ускорение, обу- |
||||||||
словленное вращением Земли вокруг собственной оси и вокруг |
||||||||
Солнца. При определенных условиях этой неинерциальностью |
||||||||
можно пренебречь, но при решении многих практических задач |
||||||||
(например, запуск космического корабля) без учета этой неинер- |
||||||||
циальности не обойтись. К тому же, многие машины и меха- |
||||||||
низмы реально работают в неинерциальных системах отсчета — |
||||||||
в движущихся с ускорением вагонах, самолетах, космических |
||||||||
кораблях и так далее. |
|
|
|
|
|
|
|
|
|
Итак, посмотрим, как преобразуется основной закон механи- |
|||||||
ки — второй закон Ньютона — при переходе от инерциальной |
||||||||
системы отсчета к неинерциальной. Остановимся отдельно на |
||||||||
двух случаях: рассмотрим сначала простейший случай поступа- |
||||||||
тельного движения неинерциальной системы, а затем обсудим, |
||||||||
как видоизменяются законы механики во вращающейся системе |
||||||||
отсчета. |
|
|
|
|
|
|
|
|
|
Поступательное движение неинерциальной системы от- |
|||||||
счета. В повседневной жизни каждому из нас чуть ли не еже- |
||||||||
дневно приходится испытывать неприятные ощущения, когда при |
||||||||
резком торможении автобуса или вагона метро какая-то сила |
||||||||
бросает нас вперед. Чтобы понять происхождение этой силы, |
||||||||
рассмотрим две системы отсчета: инерциальную систему и |
||||||||
систему , которая совершает поступательное движение от- |
||||||||
носительно системы с ускорением , зависящем в общем |
||||||||
случае от времени (рис. 9.2). Пусть и — радиусы-векторы |
||||||||
z |
|
материальной |
точки |
с |
массой |
|
||
|
в |
инерциальной и неинерциальной |
||||||
|
|
|||||||
|
m |
системах соответственно, а — |
||||||
|
радиус-вектор начала отсчета систе- |
|||||||
|
|
|||||||
|
|
мы относительно системы . |
|
|||||
|
y |
|
Уравнение |
движения |
материаль- |
|||
|
|
ной точки в инерциальной системе |
||||||
O |
|
отсчета — второй закон Ньютона: |
||||||
|
|
|
|
|
|
|
|
|
|
Рис. 9.2 |
|
|
, |
|
|
|
|
где F — результирующая сила, действующая на рассматриваемую
материальную точку со стороны других тел, 2 2 — ускорение материальной точки в инерциальной системе. Координаты и скорости материальной точки в системах и связаны друг с другом соотношениями (9.1), (9.2). Если тело неподвижно
относительно , то движение этой системы приводит к переносу тела относительно . Cкорость V называется переносной скоростью. Скорость относительно системы , т. е. так и называется — относительная скорость. Наконец, скорость v в инерциальной системе носит название абсолютной ско-
9.2 ] |
Законы механики в неинерциальных системах отсчета |
169 |
рости. Надо понимать условность последнего названия: это, конечно, просто скорость относительно системы . Но — система инерциальная, в некоторой степени «привилегированная», и только в этом условном смысле скорость может быть названа абсолютной.
Продифференцировав еще раз по времени обе части равенства (9.2), получаем соотношение между ускорениями
|
(9.4) |
Здесь, соответственно, a — абсолютное ускорение, A — переносное и — относительное. Подставив полученное выражение для во второй закон Ньютона, перепишем его в виде
|
(9.5) |
Как мы видим, уравнение движения в неинерциальной системе отсчета (9.5) отличается от второго закона Ньютона в инерциальной системе (3.2) тем, что в правой части уравнения наряду с силой появляется еще добавочное слагаемое . Если ввести обозначение
ин, |
(9.6) |
то уравнение движения в неинерциальной системе примет такой же привычный вид, как и второй закон Ньютона,
ин, |
(9.7) |
где определенное равенством (9.6) добавочное слагаемое ин
называют силой инерции, конкретно — поступательной силой инерции. Далее мы познакомимся и с другими силами инерции.
В данном случае сила инерции является пространственнооднородной, т. е. сила инерции при поступательном движении
неинерциальной системы отсчета имеет одно и тоже значение для всех точек этой системы. Это следует из (9.6): сила инерции зависит только от ускорения, с которым начало неинерциальной системы движется относительно инерциальной системы .
Итак, движение относительно рассматриваемой неинерциальной системы можно исследовать двумя способами. Можно определить закон движения материальной точки в некоторой инерциальной системе, используя второй закон Ньютона в его стандартном виде, а затем пересчитать его относительно неинерциальной системы, т. е. получить из закона преобразования координат (9.1) (при условии, конечно, что закон движения неинерциальной системы известен). Но можно сразу решать задачу в неинерциальной системе отсчета с помощью видоизмененного второго закона Ньютона (9.7), в котором в правой части к реальной силе , определяемой взаимодействием рассматриваемого тела с другими телами, добавлена сила инерции ин, опре-
170 |
Законы механики в неинерциальных системах отсчета |
[ Гл. 9 |
деляемая соотношением (9.6). Появление этой добавочной силы при рассмотрении движения относительно неинерциальной системы отсчета — формальное следствие преобразования координат (8.7) и не отражает появления какого-либо нового воздействия на материальную точку со стороны других тел.
В этом смысле силу инерции можно назвать фиктивной силой, хотя для наблюдателя в неинерциальной системе она будет приводить к таким же последствиям, как и реальная сила той же величины.
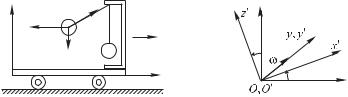
Мы уже упоминали об ощущениях наблюдателя в неинерциальной системе (в автобусе, например), связанных с ее торможением или ускорением. Поясним еще действие рассмотренной силы инерции на следующем примере. Рассмотрим тележку с укрепленным на ней кронштейном, к которому подвешен на нити шарик (рис. 9.3). Пока тележка покоится или движется без ускорения, нить расположена вертикально и сила тяжести уравновешивается натяжением нити н. Приведем теперь тележку в поступательное движение с ускорением . Нить отклонится от вертикали на такой угол, чтобы результирующая сил ин сообщала шарику ускорение, равное , т. е. в инерциальной системе отсчета угол отклонения нити определяется условием, которое, как и должно быть, является следствием второго закона Ньютона. В неинерциальной системе отсчета, связанной с тележкой, шарик покоится, несмотря на то, что результирующая сил и н отлична от нуля. Отсутствие ускорения шарика по отношению к этой системе отсчета можно формально объяснить
z |
Fí |
|
F |
|
èí |
|
A |
|
P |
O |
x |
|
z |
x |
Рис. 9.3 |
Рис. 9.4 |
тем, что кроме сил и н, равных в сумме , на шарик
действует еще и сила инерции ин .
Силы инерции во вращающейся системе отсчета. Рассмотрим теперь случай вращающейся неинерциальной системы и для определенности рассмотрим ситуацию, когда неинерциальная система вращается с угловой скоростью вокруг оси , совпадающей с осью инерциальной системы . Будем полагать также, что начала отсчета этих систем совпадают (рис. 9.4). Наша цель — записать уравнение движения материальной точки в неинерциальной системе в виде второго закона Ньютона (9.7).
