студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

6.1 ] Индуктивность и взаимная индукция 281

Коэффициенты при токе в формулах (6.1) и (6.2), как нетрудно видеть, идентичны:

Величины +12, +21 называются взаимной индуктивностью или коэффициентами взаимной индукции, а правило их равенства — теоремой взаимности, которая часто используется

при решении задач или инженерных расчетах. Легко видеть, что эти коэффициенты зависят только от геометрии контуров, с точностью, впрочем, до знака, который задается направлением обхода в интегралах (6.1)–(6.3). Его, как правило, выбирают так, чтобы все величины + были положительны, за исключением тех случаев, когда приходится суммировать магнитные потоки разного знака.

Теперь представим себе единственный замкнутый контур, по которому протекает ток :. Так же, как и в предыдущем примере, представим магнитный поток через контур, обязанный собственному току : в виде

где , . Величина + называется индуктивностью контура или коэффициентом самоиндукции. Единицу измерения

индуктивности или взаимной индукции принято называть генри; ее размерность: 1 Гн = 1 В с/А. Причина именно такого выбора размерности прояснится ниже (см. закон Фарадея). Другое определение той же единицы: 1 Гн = 1 Вб/А. Как и фарада для измерения емкости, единица эта очень велика, поэтому фактически используются микрогенри или даже наногенри; последняя совпадает с очень хорошей точностью с единицей измерения индуктивности в системе СГС, а потому часто называется сантиметром.

Определение самоиндукции (6.4) удобно постольку, поскольку следует общему алгоритму (6.3), демонстрирует явно зависимость только от геометрии контура, но никогда не используется, в отличие от (6.3), для фактического расчета индуктивности. Дело в том, что именно при рассмотрении самоиндукции неадекватно приближение линейности контура. Как следствие, интеграл (6.4) оказывается несобственным.

Это впрочем, легко понять и на более элементарном уровне: вблизи идеально тонкого провода G 1 , а значит, поток через контур расходится логарифмически. Но формула (6.4) удобна для доказательств общего вида, в чем мы еще убедимся в следующей главе; теперь же дадим два простых примера прямого вычисления индуктивности.

282 Электромагнитная индукция [ Гл. 6

1. Индуктивность коаксиальной линии. На рис. 6.1 представлена система двух соосных проводников. Ток течет по внутреннему цилиндрическому проводнику

иазимутальной симметрии системы.

Всилу тех же аргументов, между цилиндрами поле идентично полю прямого провода. Отсюда нетрудно вычислить и поток, взяв

ницу длины коаксиальной линии.

2. Индуктивность соленоида. Пусть дан длинный соленоид, без сердечника или с магнитомягким сердечником, с плотной намоткой (см., например, рис. 4.2); радиус соленоида , длина , полное число витков !, число витков на единицу длины !, магнитная проницаемость сердечника 1. Согласно выражению (4.13), внутри соленоида 110: Определяя поток через контур, следует принять во внимание, что каждая силовая линия охватывается обмоткой соленоида ! раз:

6.2. Принцип Ленца. Закон Фарадея

Из школьного курса химии известен принцип ле Шателье– Брауна, сформулированный французским ученым ле Шателье (1850–1936) и немецким физиком К.Ф. Брауном (1850–1918). Этот принцип в простейшей форме выглядит следующим образом: если некая смесь веществ пребывает в динамическом

6.2 ] Принцип Ленца. Закон Фарадея 283

равновесии за счет встречных экзо- и эндотермической реакций, то при нагревании быстрее начинает идти эндотермическая реакция, а при охлаждении — экзотермическая. В электродинамике близкий по идее принцип был сформулирован знаменитым рос-

сийским ученым-естественником Э. Х. Ленцем.

Токи, возникающие в проводнике при движении его в магнитном поле, направлены так, что силы, действующие на эти токи, противодействуют движению проводника. С уче-

том иных возможностей изменения магнитного потока может

быть предложена более общая формулировка.

Отклик динамической системы на перестройку магнитного поля всегда имеет тенденцию противодействовать этой перестройке.

Если уронить медную или серебряную монетку между полюсами мощного электромагнита, то невооруженным глазом можно наблюдать замедление — даже весьма значительное — скорости по сравнению со свободным падением. Это «работают» магнитное давление и натяжение силовых линий (см. гл. 7). Основная причина того, что эти механизмы вступают в игру, может быть связана с принципом Ленца. Равным образом объясняются этим принципом токи Фуко (по имени французского физика-экспе- риментатора Ж.Б.Л. Фуко (1819–1868)) в железном сердечнике трансформатора (из-за которых его обычно набирают из отдельных пластин) и работа динамомашины. Заметим что в первом из этих двух случаев нет ни движения проводника в поле, ни деформации контура, но лишь осцилляция магнитного поля в сердечнике как следствие непостоянства тока. Это и соответствует второй — более общей — формулировке принципа Ленца. Приходится, однако, встречаться с очень грубой его трактовкой, типа «реакция противоположна воздействию». Если бы это было правильно, то в природе, например, не существовало бы ни пара-, ни ферромагнетиков, но лишь диамагнетики. Потому и существенна оговорка относительно реакции динамической системы. Ларморова прецессия и вызванный ею диамагнетизм, и в самом деле, вполне согласуются с правилом Ленца, но, к примеру, ферромагнитные явления уже не могут быть сведены к такой схеме.

Круг явлений, подпадающий под принцип Ленца, принято называть электромагнитной индукцией. Основной количествен-

ный закон здесь был установлен английским физиком Майклом Фарадеем (1791–1867). Пусть имеется замкнутый контур любой природы (проводящий или непроводящий — даже мысленно очерченный), и пусть по любой причине — движение, деформация, затухание тока в контуре, изменение внешнего магнитного поля — изменяется во времени магнитный поток через означен-

284 Электромагнитная индукция [ Гл. 6

ный контур. Тогда в контуре возникает ЭДС , которая может быть найдена из соотношения:

Знак в (6.7) отражает то обстоятельство, что возбуждаемая

вконтуре ЭДС индукции по направлению такова, что противодействует изменению магнитного потока. В частности, при идеальной проводимости контура поток, который им охватывается, должен быть инвариантом. Это относится как к тому случаю, когда охватывающий контур является сверхпроводящим, так и к тому, когда пространственные и временные´ масштабы задачи позволяют считать его идеальным проводником. (Эти две ситуации не следует путать; мы еще вернемся к этому вопросу

вгл. 9.)

Из (6.7) следует введенная в гл. 4 размерность магнитного потока 1 Вб 1 А с Ом По этому поводу следует, впрочем, заметить, что расшифровка единиц в системе СИ в принципе может быть любой, которая не противоречила бы их определению, но обычно предпочитают пользоваться размерностью, следующей из наиболее употребительных законов и по возможности не опирающейся на размерность «вакуумных» констант 10 и <0.

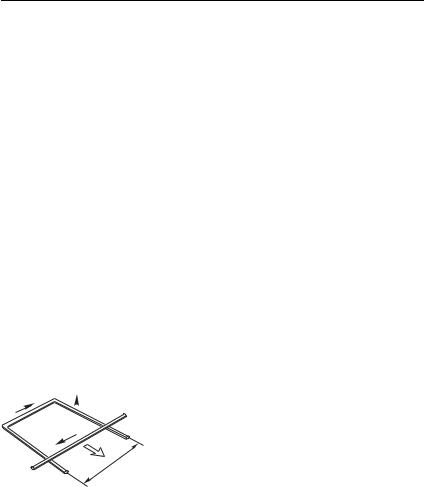
В некоторых простых случаях соотношение (6.7) может быть получено как следствие уже известных законов. Поставим следующий мысленный эксперимент (рис. 6.2): имеется проводящий

чит, на него действует сила Лоренца D Как уже не раз отмечалось, это означает, что в системе отсчета, связанной с перемычкой, возникает электрическое поле Отсюда циркуляция И поскольку , отсюда как раз следует формула (6.7). В общем случае, однако, ее не удается вывести, так что этот закон должен рассматриваться как опытный факт.

Полезно лишний раз отметить (см. рис. 6.2), что ток, порождаемый индукционным электрическим полем, в свою очередь, порождает магнитное поле, по направлению противоположное внешнему полю B, и тем самым как бы «старается»

скомпенсировать увеличение магнитного потока через контур — в согласии с принципом Ленца. При обратном направлении движения рамки генерируется поле того же направления, что и приложенное извне.

6.3. Интегральная и локальная форма закона электромагнитной индукции

Рассмотренные до настоящего момента законы электродинамики явно распадаются на две группы. В одну из них входят так называемые материальные соотношения: закон Ома, зависимость P(E) или J(B) и т. д. Эти законы задаются физикой строения вещества; результаты, на них основанные, всегда не универсальны, причем это общее свойство их всех, а не только простых линейных моделей.

Вторая группа — чисто электродинамические законы, например теорема Гаусса или теорема о циркуляции (которую, правда, нам еще предстоит записать в окончательном виде). Эти законы, разумеется, также имеют свою область применимости, но она гораздо шире, чем у материальных соотношений, по сути, оставаясь в рамках классической физики, мы за нее заведомо не выходим. Более того, эти фундаментальные законы более совершенны, нежели закон Кулона или закон Био и Савара, их породившие, поскольку не связаны приближениями точечных зарядов или бесконечно тонких элементов тока. Справедливость их подтверждается как прямыми экспериментами, так и (даже в большей степени) согласованностью и непротиворечивостью всего массива информации, составляющего основу современной электродинамики.

Опыт показывает, что закон электромагнитной индукции (6.7) также относится к этой группе фундаментальных законов. Его, конечно, имеет смысл модифицировать применительно к системе с сосредоточенными параметрами — токовому контуру —

если его параметры не меняются во времени, если же контур является перестраиваемым или, скажем, деформируемым, то соотношение (6.8) допускает естественное обобщение:

В то же время, как и для всех законов такого рода, желательно получить локальную форму закона Фарадея, которая была бы свободна от понятия какого-либо материального контура.

Для этого воспользуемся уже упоминавшейся в гл. 4 теоремой Стокса:

rot

—циркуляция вектора по некоторому контуру равна потоку ротора этого вектора через любую гладкую поверхность, натянутую на контур. Объединяем теорему Стокса и закон Фарадея:

Ввиду произвольности контура и натянутой на него поверхности, можно просто приравнять подынтегральные выражения. Только временную´ производную надо будет представить в виде частной производной по времени, чтобы избежать в локальной

форме уравнения эффектов, связанных, например, с движением вещества. Итак, вот локальная форма закона Фарадея:

Знак « », который мы до сих пор старательно удерживали как символ направленности ЭДС индукции, приобрел в этой векторной формуле окончательный смысл. В зависимости от конкретной задачи, может быть использована любая форма закона электромагнитной индукции (6.7)–(6.10), но именно (6.10) представляет закон Фарадея в наиболее общем виде.

Задачи

1. На один сердечник намотаны две катушки (рис. 6.3). Индуктивности их равны соответственно 1 0,5 Гн и 2 0,7 Гн. Чему равна их взаимная индуктивность в отсутствие рассеяния магнитного потока?

Решение. Поскольку магнитный поток не рассеивается (это означает, помимо надлежащей геометрии сердечника, ! 1), то через каждый виток он один и тот же: . Пусть, для опреде-

ленности, ток течет через первую обмотку:

Простая формула 1 2 1 2 представляет собой максимально возможный коэффициент взаимной индукции при заданной индуктивности двух катушек. Реально он всегда меньше, потому что невозможно полностью исключить рассеяние магнитного потока.

2. Внутри длинного соленоида с плотностью намотки , вдали от его концов, расположен параллельно оси намагниченный стержень с магнитным моментом . Найти магнитный поток , пронизывающий соленоид.

6.4 ] Задачи 287

Решение. Прямое вычисление было бы громоздким, и в нем легко было бы ошибиться. Но мы можем сделать мысленно совершенно эквивалентную замену. Пусть вместо постоянного магнита в соленоид помещен виток с током, так что +( Далее мы можем воспользоваться теоремой взаимности, пропустив ток + не через виток, а через обмотку соленоида. Тогда!0+ !0 (, и магнитный поток через виток, как раз и равный искомому, составляет !0 Представляется достаточно нетривиальным факт универсальности ответа; без теоремы взаимности установить его было бы затруднительно.

3. В ускорителе электронов — бетатроне — роль ускоряющего напряжения играет ЭДС индукции, возбуждаемая изменением магнитного потока, пронизывающего орбиту электрона. Электроны же при этом движутся по орбитам примерно постоянного радиуса. Определить необходимое для этого соотношение между средним по полощади орбиты магнитным полем , пронизывающим орбиту электрона, и магнитным полем 0 непосредственно

на орбите. Поле считать нормальным к плоскости орбиты.

Решение. Если частица движется по круговой орбите, то, согласно (4.8), частота обращения есть <0 . При импульсе частицы & радиус орбиты равен & <0. Условие эквивалентно следующему:

& 0 или, что то же, & & 0 0. Ускорение электрона на орбите постоянного радиуса происходит в соответствии с законом & <*, где электрическое поле определяется из закона Фарадея (6.7):

2* 2

Таким образом, зависимость * 2 подставляется в соотношение

0 <*0 <0

Отсюда следует 0 1 2 в любой момент времени, что эквивалент-

но 0 2.

4. Один и тот же ток идет по двум параллельным проводам в противоположные стороны. Провода имеют круглые сечения радиуса # 2 мм, а расстояние между ними 2 см. Найти индуктивность единицы длины такой системы, учитывая поле только вне проводов.

Какой заряд 9 пройдет через любое сечение провода рамки, если она повернется вокруг ближайшей к проводу стороны ) на угол и останется в этом положении? Сечение провода рамки (, удельное сопротивление %. Самоиндукцией рамки пренебречь.

Г л а в а 7

ЭНЕРГИЯ И СИЛЫ В МАГНИТНОМ ПОЛЕ

7.1. Проводники в магнитном поле. Магнитное давление

Стем, что такое магнитное давление, мы уже познакомились

взадаче 2 гл. 4. Напомним, что поле между проводящими плоскостями было равно G , где — линейная плотность поверхностного тока, а давление на каждую плоскость составляло

2

!0C

вн 2

Нетрудно сообразить, что такое же точно давление будет действовать на любую плоскую поверхность проводящего тела, если вне тела существует магнитное поле B, параллельное поверхности, а в самом теле 0. Действительно, величина однозначно следует из теоремы о циркуляции, и все последующие соображения остаются в силе. Нужно только переписать формулу для давления на поверхность проводника, исходя из того, что задано все-таки именно поле в вакууме:

Существенно, во-первых, то обстоятельство, что магнитное давление обусловлено «непроникновением» магнитного поля в проводник. Если последний пребывает в сверхпроводящем состоянии, это всегда верно, но и в обратном, гораздо более обыденном случае, это совершенно реально. Как мы увидим далее (см. гл. 8), проникновение поля в проводящую среду — процесс не мгновенный, и чем выше проводимость, тем более он затянут во времени.

Во-вторых, при выводе формулы (7.1) мы использовали упрощенную геометрию: внешнее поле, параллельное плоской поверхности проводника. Это сужает круг явлений, которые мы могли бы обсуждать, либо создает опасность ошибок, проистекающих от расширительного толкования результата (7.1).

Прежде чем давать формальное описание сил, действующих в магнитном поле на проводящую среду, приведем чрезвычайно удобную форму для архимедовой силы, использующую операцию векторного дифференцирования. Рассмотрим некоторую текучую

кривизной силовых линий. Это не значит, что они должны быть непременно прямыми — просто радиус их кривизны должен быть много больше толщины слоя, в котором магнитная индукция B меняется на величину порядка ее самой. Вот пример ситуации, когда натяжением пренебречь нельзя: магнитное поле в проводнике установилось таким образом, что токи в нем не текут. Допустим, вне проводника проходит прямой провод с током, и поле в проводящей среде соответствует формуле (4.9). Из (7.1), казалось бы, следует, что в проводнике возникает некоторый перепад давлений, а значит, и силы. Но из формулы (4.6) следует, что при 0 должно быть и 0. Действительно, можно показать, что в этом случае два члена в правой части (7.3)

вточности компенсируют друг друга.

2.Возможная причина недоразумений — независимость формул (7.1) и (7.3) от проводимости среды. На первый взгляд может показаться, что и на диэлектрик должно действовать точно такое же давление. В этой связи полезно напомнить, что при выводе (7.3) мы существенным образом воспользовались двумя предположениями: теоремой о циркуляции: и линейной зависимостью B(H). Как уже было замечено в гл. 4, теорема о циркуляции у нас пока не дописана; в нестационарном случае

вправой части появится еще один член (и добавим, забегая вперед, — роль его будет тем важнее, чем ниже проводимость вещества). Таким образом, для настоящего диэлектрика наш вывод справедлив только при условии абсолютной стационарности задачи, и, поскольку тока проводимости в непроводящем веществе просто не может быть, два члена в правой части (7.3) обязаны при этом точно друг друга компенсировать. Тем самым определяется класс допустимых магнитных конфигураций в линейном диэлектрике.

Положение дел меняется, если мы имеем дело с магнитоактивной средой (линейная зависимость B(H) представляет не более, чем частный случай). Тогда к силам Ампера, обязанным своей природой токам проводимости, добавятся силы, обусловленные намагниченностью образца. Это и будет темой последующего рассмотрения.

7.2. Диполь в магнитном поле

Хотя векторная природа электрического и магнитного полей различна и магнитный дипольный момент (4.21) определяется иначе, нежели электродипольный момент (1.23), обращает на себя внимание тождественность выражений для поля (4.24) и (1.25). Из рис. 4.4 можно усмотреть совершенную идентичность картины поля при переходе к приближению точечных диполей.