
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
12.5 ] |
Задачи |
381 |
диэлектрическую проницаемость (12.20), получаем 0. — это не что иное, как ленгмюровские колебания, рассмотренные в предыдущем параграфе на основании более простой модели.
Задачи
1. Плоский конденсатор заполнен плазмой со средней концентрацией электронов и ионов 0 и температурой . Расстояние между пластинами , разность потенциалов . Пренебрегая током в плазме и считая < Б , определить пространственную зависимость потенциала между обкладками.
Решение. Из механики известна барометрическая формула Больцмана
0 ,
Б
где — масса отдельной молекулы, — ускорение силы тяжести, ось 0 направлена вертикально вверх. Эта формула — частный случай гораздо более общего закона, который называется статистическим распределением Больцмана. В случае произвольной потенциальной функции он имеет вид
0 |
|
|
|
|
Б |
||||
|
|
|||
Распределение Больцмана для электронов и ионов в нашем случае можно линеаризовать:
0 |
< |
|
|
0 1 |
< |
|
; |
||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
Б |
|
|
Б |
|||||
0 |
< |
|
0 1 |
< |
, |
||||||||
|
|
|
|||||||||||
|
|
|
|
Б |
|
Б |
|||||||
а затем подставить в уравнение Пуассона: |
|
|
|
|
|
|
|||||||
2 |
< |
|
|
|
2<2 |
|
2 |
|
|||||
|
2 |
0 |
|
|
2 |
||||||||
|
0 |
|
00 Б # |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
Уравнение получилось линейным и однородным, поэтому его решение в точности соответствует формуле (8.9), только в данном случае корни характеристического уравнения вещественны:
1 |
2 |
|
2 |
2 |
|
|
|
|
|||||
|
#D |
|
|
#D |
|
|
Принимая во внимание граничные условия
0, 0; , ,
приходим к следующему ответу:
2 #D
2 #D
Таким образом, на этой относительно простой одномерной задаче мы продемонстрировали, что из объединения электростатики с тепловым движением частиц в плазме действительно рождается пространственный масштаб #D — дебаевская длина.

382 Элементы физики плазмы [ Гл. 12
2. Площадь электродов плоского газонаполненного диода ( 10 см2, межэлектродный зазор 10 см. В режиме несамостоятельного разряда ток на-
сыщения + 10 6 А. Какое количество элементарных зарядов того и другого знака создается ежесекундно внешним ионизатором в 1 см3?
Ответ: |
B |
+ |
6 109 см 3 с 1 |
|
<( |
|
|
3. Мощный источник тока создает в тонкой цилиндрической плазменной |
|||
оболочке ток |
+ 5 106 А, параллельный оси и равномерно распределен- |
||
ный по азимуту. Внутри оболочки предварительно создано магнитное поле0 0,1 Тл. Начальный радиус цилиндра 0 20 см. В дальнейшем под действием тока оболочка сжимается по радиусу. Считая ее идеально проводящей, оценить, при каком радиусе ускорение оболочки поменяет знак.
2 |
|
|
Ответ: |
2 0 0 |
4 мм |
|
||
!0+ |
|
|
4. В плазме находится дипольный излучатель, на который подается переменное напряжение с частотой При какой концентрации электронов плазмы он перестает излучать электромагнитные волны?
2
Ответ: E 00 <2
5. Электромагнитная волна падает на поверхность плазмы, концентрация которой растет вглубь, а на поверхности много меньше критической. Угол падения равен $. Какой концентрации плазмы соответствует поверхность, от которой произойдет отражение? Будет ли угол отражения равен углу падения?
|
00 |
2 |
|
|
Ответ: угол отражения будет равен углу падения, |
2 |
$. |
||
|
|
|
||
<2 |
|
|
|
|

Р а з д е л т р е т и й
ФИЗИКА КОЛЕБАНИЙ И ВОЛН. ВОЛНОВАЯ ОПТИКА
ВВЕДЕНИЕ
Раздел посвящен изучению колебательно-волновых закономерностей, пронизывающих всю современную физику. В механике и акустике, в радиофизике и оптике, в квантовой физике
ифизике твердого тела — всюду мы сталкиваемся с колебаниями и волнами. Здесь особенно ярко находит отражение современная тенденция сближения и взаимопроникновения различных областей науки. Единый подход к изучению колебаний и волн различной физической природы, основанный на общности уравнений, описывающих колебательно-волновые закономерности, позволяет выявить глубокие связи между различными, на первый взгляд, явлениями. Этот подход оказался плодотворным по крайней мере в двух отношениях. Во-первых, он позволил обобщить и распространить на различные области физики идеи
иметоды, возникшие первоначально в какой-либо одной области (например, распространить идею Габора электронной голографии сначала на оптическую, а затем на радио- и акустическую голографию). Во-вторых, он позволил выявить плодотворные колеба- тельно-волновые аналогии: идеи и методы решения задач физики колебаний перенести на задачи волновые и наоборот (например, фильтрация временных сигналов-колебаний и пространственная фильтрация волн). Знания и интуиция, которые мы приобретаем при изучении колебаний и волн одной физической природы естественным образом используются при изучении явлений казалось бы совершенно иной природы. Например, изучая поведение волн света, мы начинаем глубже понимать, как ведут себя «волны вероятности», которыми оперирует квантовая физика, или волны звука, которые изучаются в акустике. Таким образом, изучая колебания и волны, мы будем обращать внимание не только на то, что «волнуется» и что «колеблется», а главным образом на то, как и почему происходят колебания и возникают волны.
Г л а в а 1
КИНЕМАТИКА КОЛЕБАНИЙ
1.1. Гармонические колебания
Колебание — это более или менее регулярно повторяющийся процесс. Таково очень нестрогое, «качественное» определение понятия «колебание». Можно привести множество примеров колебательных процессов, относящихся к различным областям физики (и не только физики). Колеблется маятник часов; колеблется груз, подвешенный на пружине; колеблется взволнованная поверхность воды и гитарная струна; колеблется заряд на пластинах конденсатора и магнитное поле в катушке индуктивности колебательного контура; более или менее периодически изменяется температура воздуха (зимой холоднее — летом теплее) и количество автомобилей на улицах города (больше в часы пик — меньше поздней ночью); периодически меняется экономическая ситуация в жизни общества: кризисные явления сменяются подъемом экономики. Колеблется давление (или плотность воздуха), вызывая колебания ушной мембраны —
имы слышим голос певца на оперной сцене. Таких примеров можно привести как угодно много. В настоящей главе мы не будем выяснять причины возникновения колебаний в той или иной физической системе. Здесь мы лишь познакомимся с наиболее часто встречающимися простейшими видами колебательных движений, основными характеристиками колебательных процессов, с математическим способом описания колебаний. Оставляя пока в стороне физическую природу колеблющейся величины, будем обозначать ее буквой 9, подчеркивая при этом, что любой колебательный процесс развивается во времени: 9 9 . (Величиной 9 может быть и угол отклонения маятника часов,
ивеличина растяжения-сжатия пружины при колебаниях груза,
иизменяющийся заряд на пластине конденсатора, и плотность воздуха при распространении звуковой волны. В общем, 9 — любая колеблющаяся величина.)
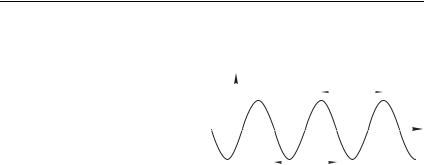
Наиболее простая функция, описывающая периодический процесс, имеет вид
9 , |
(1.1) |
где , и — константы. Функциональную зависимость (1.1) физики называют уравнением гармонических колебаний, ее гра-
386 |
Кинематика колебаний |
[ Гл. 1 |
строго говоря, описываться функцией вида (1.1). Ведь синусоида не имеет ни начала, ни конца — и хотя бы поэтому бесконечно длящийся колебательный процесс неосуществим.
1.2. Векторная интерпретация и комплексное представление гармонических колебаний.
Фазовая плоскость
Векторная интерпретация. При решении многих задач, связанных с изучением колебательных процессов, удобно использовать следующую геометрическую интепретацию гармонических колебаний.
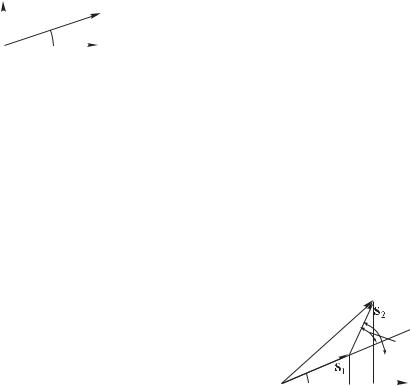
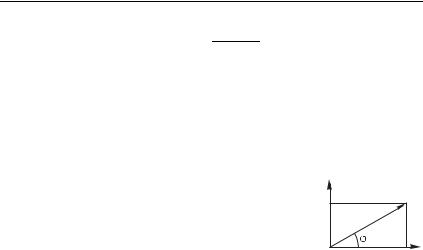
Гармоническое колебание (1.1) будем изображать вектором ,
длина которого равна амплитуде колебания , а угол между |
||||
|
y |
|
|
вектором и горизонтальной осью — на- |
|
|
|
S чальной фазе колебания (рис. 1.2). |
|
|
|
|
||
|
a |
|
|
|
|
|
|
При этом частота гармонического ко- |
|
|
|
x |
||
|
лебания предполагается заданной. Смысл |
|||
|
|
|
|
|
O |
|
|
такого представления состоит в следую- |
|
|
Рис. 1.2 |
|
|
|
|
|
|
щем. Вообразим, что вектор вращается |
|
вокруг точки с угловой скоростью в положительном направлении, т. е. против часовой стрелки, а мы сделали мгновенную фотографию в момент времени 0, когда угол наклона вектораравен . Заметим, что проекция вектора на осьпри вращении изменяется по закону , т. е.
совершает гармонические колебания.
Геометрическое изображение гармонического колебания 9
в виде вектора удобно использовать при решении задачи сложения колебаний. Пусть мы имеем две скалярные величины 91
и 92, изменяющиеся по гармоническому закону с одинаковой частотой :
91 1 1 , |
92 2 2 |
|
|
|
||||
Необходимо найти колебание 9 (скалярную величину), |
||||||||
являющуюся суммой колебаний 91 и 92 : |
|
|
|
|
|
|||
9 91 92 |
(1.6) |
|
|
S |
2 |
|
||
Изобразим колебания 91 и 92 |
|
|
|
|
|
|||
|
|
|
|
|
||||
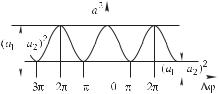
в виде векторов 1 и 2 (рис. 1.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Изобразим также суммарный вектор S. |
1 |
|
|
|
x |
|||
Векторы 1, 2 и S образуют треуголь- |
|
|
|
|||||
O |
|
|
|
|
|
|
||
ник, причем внешний угол треугольни- |
|
Рис. 1.3 |
|
|
|
|||
ка равен разности фаз колебаний |
|
|
|
|
||||
|
|
|
|
|
|
|
||
92 и 91. Представим себе, что |
векторы |
1 и 2 |
вращаются |
|||||
с одной и той же угловой скоростью против часовой стрелки.
388 |
Кинематика колебаний |
[ Гл. 1 |
Фазовая плоскость. При изучении колебаний полезным
оказывается изображение колебательного процесса на фазовой плоскости. Координаты на фазовой плоскости — величина 9
(ось абсцисс) и производная по времени 9 (ось ординат). В каждый момент времени с помощью соотношений
9 |
, |
(1.9) |
|
|
|
9 |
|
|
можно найти значения 9 и 9 и, следовательно, положение точкина фазовой плоскости, изображающей состояние колебательной системы в данный момент времени. С течением времени величины 9 и 9 изменяются (в соответствии с (1.9)), изменяется,
следовательно, и положение изображающей точки, которая описывает так называемую фазовую траекторию. Уравнение фа-
зовой траектории гармонического колебательного процесса легко найти, исключая из уравнения (1.9) время :
( |
2 |
2 |
|
|
|
|
|
( |
|
|
1 |
(1.10) |
|
|
2 |
|
2 |
|||
|
|
|
|
|
||
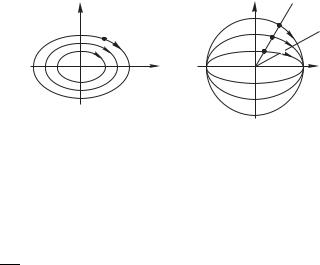
Согласно (1.10), фазовая траектория гармонического колебания — эллипс с полуосями и . Из (1.9) ясно, что изображающая точка движется по фазовой траектории по часовой стрелке.
На рис. 1.5 а изображено семейство фазовых траекторий, отличающихся амплитудой колебания.
|
. |
|
. |
|
S, 2 ñì/ñ |
3 |
S A |
2 |
|
2 |
M3 |
M |
M2 |
||
|
|
B |
|
|
|
1 |
|
1 |
|
M1 |
|
|
|
|
|
0 2 3 4 S, ñì |
0 |
S |
|
à |
|
á |
|
Рис. 1.5
Комплексная форма записи гармонических колебаний.
В дальнейшем при исследовании колебаний мы часто будем использовать комплексную форму записи гармонических колебаний. Напомним, что комплексное число может быть записано в виде
, |
(1.11) |
1 — мнимая единица, и — собственно действительная

390 Кинематика колебаний [ Гл. 1
Комплексное число D называется комплексной амплитудой колебания. Она содержит информацию как об амплитуде
колебания, так и о начальной фазе.
Числа 1 и 2 называются комплексно-сопряженными, если их действительные части равны, а мнимые отличаются знаком:1 , 2 . Комплексно-сопряженные числа имеют одинаковые модули и аргументы противоположного знака:
1 D , 2 D . Тот факт, что числа 1 и 2 являются комплексно-сопряженными принято записывать в виде: 1 2 .
1.3. Некоторые важные задачи сложения гармонических колебаний
Рассмотрим задачи сложения гармонических колебаний, необходимые как для дальнейшего углубленного изучения общих вопросов теории колебаний, так и для решения конкретных
волновых задач.
1. Сумма N колебаний, фазы которых составляют арифметическую прогрессию
|
|
9 0D 1 ' 0 0D' 0D 2' |
(1.15) |
1
Построим векторную диаграмму (рис. 1.7). Первое слагаемое в (1.15) изображается вектором длины 0, направленным вдоль
|
|
|
|
действительной |
оси; |
второе |
слагаемое |
|||||
|
|
|
|
0D' — вектор той же |
длины, составляю- |
|||||||
|
|
|
|
щий угол # с действительной осью; третий |
||||||||
|
|
|
|
вектор |
составляет с действительной |
осью |
||||||
S |
угол 2# (и угол |
# со |
вторым |
вектором) |
||||||||
|
|
|
N |
и |
т. д. |
Суммарное колебание — вектор , |
||||||
|
|
|
||||||||||
|
|
|
|
проведенный из начала 1-го вектора в конец |
||||||||
R |
|
последнего !-гo |
вектора. |
Складываемые |
||||||||
|
|
|
|
векторы |
образуют часть |
равностороннего |
||||||
|
|
|
|
многоугольника, вписанного в окружность, |
||||||||
|
a0 |
|||||||||||
|
радиус которой равен 0 2 #2 . |
|||||||||||
Рис. 1.7 |
||||||||||||
|
Из векторной |
диаграммы легко |
найти |
|||||||||
|
|
|
|
модуль вектора : |
|
|
|
|
|
|||
2 |
2 B |
2 B |
0 |
B2 |
, |
(1.16) |
||||||
2 |
2 |
|||||||||||
|
|
|
|
|
2 |
|
|
|
||||
