студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

Равенства (2.98) и (2.99) лежат в основе спектрального анализа линейных колебательных систем. Они позволяют найти спектр вынужденных колебаний, т. е. либо набор коэффициентов (в дискретном случае), либо непрерывный спектр , если известен спектр внешней силы и частотная характеристика колебательной системы.

Для иллюстрации изложенного метода рассмотрим одну из

важных проблем, которая решается с помощью линейных фильтров — проблему селекции, которая возникает, в частности, при

приеме радиосигналов.

Пусть на вход колебательного контура приемника поступают сигналы двух радиостанций, ведущих передачи на несущих частотах 0 и 1. Это модулированные колебания

7- 1 0 1

и

7 2 1 2

Их спектры — %- и % . Требуется выделить полезный сигнал 7- и отсеять помехи (сигнал 7 ).

Требования, предъявляемые к частотной характеристике контура вытекают из соотношений (2.98) и (2.99). Во-первых контур необходимо настроить на несущую частоту сигнала 7- , т. е. резонансная частота контура р должна совпадать с 0: р 0. При этом добротность контура C должна быть достаточно большой, чтобы в пределы полосы пропускания контура 0C не попали спектральные компоненты помех 1, 1 0 & . С другой стороны, чтобы полезный сигнал был принят без искажений, необходимо, чтобы полоса частот полезного сигнала, определяемая характерным временем > изменения функцийи , описывающих закон модуляции ( > 2$ — соотношение неопределенностей), была меньше полосы пропускания контура ' .

Всем этим условиям удовлетворяет частотная характеристика, показанная на рис. 2.21 (показаны дискретные спектры %- и % сигналов 7- и 7 ).

Спектр выходного сигнала находим с помощью (2.99)

%- % G %- G р C %-

(спектральные компоненты на частотах 1 оказываются подавленными, поскольку % G 0).

Действительно, из выражения для частотной характеристики резонансного контура следует (при 0 1): G 1 при

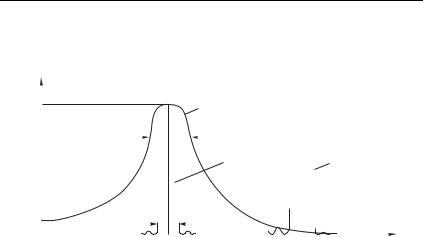
2.8 ] Спектральный анализ линейных колебательных систем 453

р, G C при р и G 0 2 при р.

Таким образом, выходной сигнал оказывается отфильтрованным: он содержит лишь спектральные компоненты полезного сигнала 7- .

Демодуляция и квадратичное детектирование. После того как с помощью линейного фильтра осуществлена задача селекции — выделение из множества сигналов интересующего нас полезного сигнала (модулированного колебания 70 ) необходимо решить проблему демодуляции — преобразования высокочастотного колебательного процесса 7 (гармонические составляющие которого заполняют интервал частот 0 ' ' 0 в окрестности несущей частоты 0) в низкочастотные звуковые колебания и , содержащие непосредственно передаваемую информацию (речь, музыка, телевизионное изображение и т. п.). Такую трансфор-

мацию частот невозможно осуществить с помощью линейного фильтра. Мы рассмотрим метод квадратичного детектирования.

Идеальный квадратичный детектор имеет вольт-амперную характеристику 2 2. Демодулятор должен включать в себя также инерционное устройство, реагирующее на низкочастотные колебания, из которых состоят законы модуляции и, но не успевающее следить за колебаниями, происходящими с частотами порядка 0.

Пусть функция , описывающая закон амплитудной модуляции, содержит низкочастотные колебания

D

Тогда модулированное колебание

7 0

содержит частоты 0 :

7 D #0 ,

а ток детектора (пропорциональный 72 ) есть

D #0 D #0

Он содержит комбинационные частоты вида 0 0 , которые распадаются на высокие частоты 2 0 и низкие частоты , за которыми только и может следить регистрирующий прибор.

Мы не будем далее интересоваться конкретным устройством демодулятора — квадратичного детектора и будем полагать, что сигнал на выходе детектора представляет собой квадрат входного сигнала, усредненный за некоторое время , определяемое инерционностью регистрирующего устройства:

2

Будем полагать, что время усреднения удовлетворяет условию

где > — характерное время изменения функций и 7 , описывающих закон модуляции сигнала 7 .

Рассмотрим примеры.

1. На вход квадратичного детектора подано амплитудно-мо- дулированное колебание 7 0 . Найдем сигнал на выходе детектора

может заметно измениться), то на интервале усредненияфункцию 2 можно считать константой, равной значению 2 в середине интервала усреднения: 2 2

2.8 ] Спектральный анализ линейных колебательных систем 455

2

Последнее слагаемое пренебрежимо мало по сравнению с первым, если интервал усреднения содержит большое число пери-

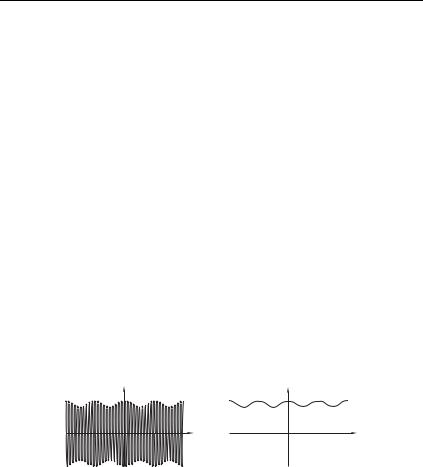
т. е. сигнал на выходе детектора содержит информацию о законе амплитудной модуляции входного сигнала.

На рис. 2.22 изображены колебания 7 и на входе и выходе квадратичного детектора при 0 1 .

Рис. 2.22

2. Пусть на вход квадратичного детектора поступает фазовомодулированное колебание

7 0 0

Сигнал на выходе детектора

2

2

Поскольку на интервале усреднения функция , описывающая закон фазовой модуляции, остается константой (равной

значению в середине интервала усреднения0), то получаем

1 2

2 0 ,

т. е. закон фазовой модуляции оказывается утерянным при квадратичном детектировании.

Решить проблему можно, исказив определенным образом ам- плитудно-фазовые соотношения в спектре фазово-модулирован- ного колебания (превратив таким образом колебание, модулированное по фазе в амплитудно-модулированное колебание). После чего искаженный таким образом сигнал можно подать на вход квадратичного детектора.

Вернемся в качестве примера к модулированному колебанию с законом модуляции (при 1). Разложение в спектр этого колебания имеет вид (см. (1.45)):

Прием без несущей. Рассмотрим прием без несущей. После устранения несущего колебания 0 0 получаем сигнал

2

закон фазовой модуляции (правда в искаженном виде) выявлен: изменение выходного сигнала детектора происходит с удвоенной

частотой:

2 2

0 1 2 (2.103)

4

Прием с изменением фазы несущей. После изменения фазы несущего колебания на $ 2:

0 0 0 0 2

2.9 ] Задачи 457

имеем

7 0 0 2

Теперь фазовые соотношения между всеми гармониками оказались такими же, как и в амплитудно-модулированном колебании (1.43). Действительно, после простых преобразований получаем

7 0 1 0

Мы преобразовали колебание, модулированное по фазе (с законом фазовой модуляции ), в амплитудно-модули-

рованное колебание 7 с законом модуляции

0 1

На выходе квадратичного детектора, согласно (2.102), получаем

т. е. переменная составляющая сигнала на выходе детектора воспроизводит без искажения закон фазовой модуляции исходного сигнала 7 .

Задачи

1.Вывести закон сохранения энергии для упругого маятника. Найти зависимость от времени кинетической и потенциальной энергии.

2.Выразить добротность колебательного контура с малым затуханием через его параметры , ; и .

3.Решить аналогичную задачу для пружинного маятника с параметрами

, и .

4.Покажите, что добротность осциллятора выражается через параметры0 и Æ с помощью равенства 9 0 2Æ.

5.Определите добротность колебательной системы, осциллограмма коле-

бания которой показана на рис. 1.15 а.

6. Найти частотные характеристики фильтров, изображенных на рис. 2.18.

всравнении с периодом свободных колебаний) магнитный поток

вкатушке сохраняется. В противном случае, если бы поток

изменялся на конечную величину за очень малое время >,

в катушке возникала бы ЭДС индукции инд > , что приводило бы к бесконечно большим токам в контуре. Учи-

тывая это обстоятельство, легко подсчитать изменение энергии контура ) (энергии катушки индуктивности) при скачкообразных изменениях индуктивности:

где +: за время >.

Окончательное выражение для ) запишем в виде

Скачкообразное уменьшение индуктивности ( + ' 0) происходит в моменты времени, когда : : . При этом в контур вносится энергия ( ) & 0), равная

Эта энергия черпается из внешнего источника: быстро уменьшить индуктивность можно, например, быстро увеличив длину катушки — растягивая ее, либо быстро извлекая из катушки железный сердечник. В любом случае для этого следует совершить работу: витки катушки притягиваются между собой амперовой силой, железный сердечник втягивается внутрь катушки. Итак, уменьшая индуктивность, мы совершаем работу, которая и идет на увеличение энергии контура, т. е. на раскачку колебаний. Скачкообразное увеличение индуктивности мы производим в моменты времени, когда ток в катушке равен нулю (моменты 2 и 4 на графике). При этом, согласно (3.1), ) 0; энергия не меняется, поскольку изменение индуктивности в этом случае происходит без совершения работы.

Поскольку подкачку энергии мы производим дважды за период, то полное увеличение энергии за период колебания равно

С другой стороны, в процессе колебаний энергия расходуется на джоулево тепло. Джоулевы потери за период

)т :2 ,

где :2 — среднее значение квадрата тока за период, которое связано с максимальным значением : известным соотноше-

нием :2 :2 2 (последнее справедливо, если контур обладает

460 Параметрические колебания. Ангармонический осциллятор [ Гл. 3

Условие параметрической раскачки колебаний — превышение подводимой энергии над потерями ) )т. С учетом (3.3) и (3.4) получаем +&2.

Последнее неравенство можно записать в виде

В последнем равенстве C — добротность колебательной системы. Если подкачку энергии осуществлять один раз за период, то для раскачки колебаний нужны вдвое большие относительные изменения индуктивности + +.

Аналогичным образом можно рассмотреть параметрическую раскачку колебаний маятника. Раскачиваясь на качелях (сгибая и выпрямляя ноги), мы по существу изменяем длину маятника.

Подумайте, каковы оптимальные моменты времени, в которые следует изменять длину маятника. Считая добротность маятника заданной, выведите условие параметрической раскачки его колебаний, аналогичное условию (3.5).

При выполнении неравенства (3.5) подводимая к колебательному контуру энергия превышает потери — амплитуда колебаний постепенно нарастает, т. е. имеет место параметрическое усиление колебаний. Естественно возникает вопрос: почему амплитуда не нарастает до бесконечности? Дело в том, что рано или поздно нарушается одно из важнейших условий, которые мы приняли при выводе уравнения, описывающего процесс колебаний, а именно, независимость параметров системы от амплитуды колебаний. В частности, омическое сопротивление контура мы полагали неизменным, не зависящим от величины протекающего тока. При достаточно больших токах это условие нарушается: сопротивление нарастает (резистор нагревается, растут джоу-

левы потери), поскольку растет температура.

нарном режиме колебаний показана на рис. 3.2: ток в катушке индуктивности / дважды за период скачкообразно нарастает