
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf

432 |
Колебания в линейных системах |
[ Гл. 2 |
Выражение в скобках — среднее за период значение магнитной энергии -м , равной (при малом затухании) половине полной энергии -0. Поэтому
- -0 2Æ-0
Вновь получаем (как и для пружинного маятника)
*0 |
9 |
, |
(2.42) |
||
* |
|
2 |
|||
|
|
||||
где C $Æ — добротность колебательного контура.
Мы рассмотрели лишь два примера, но вывод, заключенный
в равенстве (2.42), является общим для любого осциллятора с затуханием. Добротность осциллятора есть (с точностью до множителя 2$) отношение полной энергии колебаний к потерям энергии за период. Соотношение (2.42) можно считать определением понятия добротности осциллятора.
Осциллятор с большим затуханием (Æ & 0). Обратите внимание, что функция 9 , описываемая формулой (2.28), не имеет в этом случае ясного физического смысла: ведь частота
2 |
2 становится при Æ & |
0 |
мнимым числом. Итак, |
0 Æ |
|
|
прежнее решение, имеющее вид затухающего колебательного процесса, теперь не годится.
Напомним, что в теории дифференциальных уравнений предлагается следующий способ решения. Поставим в соответствие
уравнению (2.27) алгебраическое уравнение: |
2 |
2 |
Æ 2 |
0 |
||||
|
0 |
|||||||
(это уравнение называется характеристическим). Его корни |
|
|||||||
|
|
|
|
|
|
|
|
|
|
1, 2 |
Æ Æ2 2 |
|
|
(2.43) |
|||
|
0 |
|
|
|
|
|
||
действительные (при Æ & 0), причем оба корня отрицательны. Общее решение уравнения (2.27) имеет вид
9 D(1 D(2 |
(2.44) |
Непосредственной подстановкой легко убедиться, что функция (2.44) действительно является решением уравнения (2.27) при произвольных значениях констант и .
Эти две константы могут быть найдены, если заданы два начальных условия (например, функция 9 и ее производная
9 при 0).
Итак, решение представляется в виде суммы двух монотонно убывающих экспоненциальных функций (поскольку оба показателя экспонент 1 и 2 отрицательны). Ясно, что их сумма не может привести к затухающему колебательному решению (т. е. функция 9 не может, бесконечное число раз изме-
2.4 ] Затухающие колебания гармонического осциллятора 433
няя знак, проходить через нуль). Действительно, пусть, например, 1 & 2 . Очевидно, что каковы бы ни были начальные условия, при достаточно большом
будет выполнено условие D(2 |
|
|
|
||
|
|
|
|||
D(1 и решение приближенно |
|
|
|
||
(при больших |
) будет иметь |
вид |
0 |
|
|
9 D(2 , |
т. е. монотонно |
убы- |
|
|
|
|
|
t |
|||
вающее решение. Можно показать, |
|
|
|||
|
|
|
|||
что система стремится к положе- |
|
|
|
||
нию равновесия, совершив не бо- |
|
|
|
||
лее одного-двух (в зависимости от |
|
|
|
||
|
|
|
|||
начальных условий) колебательных |
|
|
Рис. 2.7 |
||
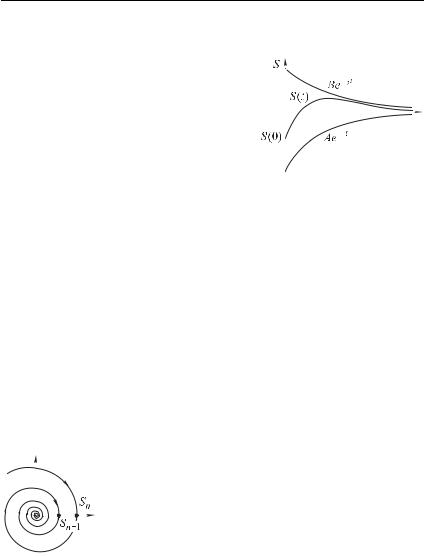
движений. Такой процесс называет- |
|
|
|
||
ся апериодическим. На рис. 2.7 приведен пример процесса 9 , представляющего собой сумму двух затухающих экспонент D(1 и D(2 (штриховые кривые).
В критическом случае Æ 0 получаем два равных корня характеристического уравнения
1, 2 Æ
В этом случае общее решение уравнения (2.27) имеет вид
9 D Æ |
(2.45) |
(проверьте непосредственной подстановкой в (2.27), что функция (2.45) является решением при произвольных и ).
Фазовая плоскость затухающего осциллятора. Напомним, что гармонический колебательный процесс на фазовой плоскости
. |
|
|
(9 — ось абсцисс, 9 — ось ординат) изоб- |
|
|
S |
|
|
ражается эллипсом, причем полуоси эллипса |
|
|
|
|
|
|
|
|
|
определяются амплитудой колебания (см. фор- |
|
|
|
|
мулу (1.10) и рис. 1.5). Качественно ясно, что |
|
|
|
|
траектория, изображающая затухающий коле- |
|
|
S |
||
|
|
бательный процесс (2.28), должна иметь вид |
||
|
|
|
|
|
|
|
|
|
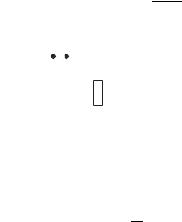
скручивающейся спирали (рис. 2.8). Действи- |
|
|
|
|
тельно, поскольку амплитуда колебания (2.28) |
Рис. 2.8 |
|
|
D Æ постепенно уменьшается, изобра- |
|
|
|
|
|
жающая точка переходит со временем с одного |
эллипса (отвечающего гармоническому колебанию с определенной амплитудой) на другой эллипс (отвечающий гармоническому колебанию с меньшей амплитудой).
Шаг спирали
1 D Æ D Æ 1 D Æ 1 D Æ1


2.5 ] |
Связанные осцилляторы |
|
435 |
|
Во всех приведенных примерах мы имеем системы с двумя |
||||
степенями свободы: для описания состояния каждой из них необ- |
||||
ходимо иметь две переменные, например, углы #1 и #2 от- |
||||
клонения маятников на рис. 2.10 а, координаты тел 1 и 2 |
||||
на рис. 2.10 б, заряды конденсаторов /1 и /2 на рис. 2.10 в. |
||||
Мы постараемся подметить общие закономерности поведения |
||||
колебательных систем с двумя степенями свободы, рассмотрев |
||||
конкретный пример. |
|
O1 |
O2 |
|
Пусть два маятника связаны пружиной |
||||
(рис. 2.11). Будем рассматривать малые коле- |
|
|
||
бания, так что #1 #1 и #2 #2. |
h |
k |
||
Пружина жесткости закреплена на рас- |
|
|
||
стоянии от точек |
подвеса маятников, |
1(t) |
2 (t) |
|
причем при #1 #2 0 пружина не дефор- |
||||
m |
||||
мирована. |
|
m1 |
2 |
|
|
|
|||
Уравнение движения (I# ) для пер- |
Рис. 2.11 |
|||
вого маятника имеет вид |
|
|
||
2 |
#1 1 1#1 #2 #1 , |
(2.46) |
1 1 |
где 1 12 — момент инерции относительно оси 1, 1 1 #11 1#1 — момент силы тяжести, #2 #1 — деформация (удлинение) пружины, 2 #2 #1 — момент упругой силы относительно той же оси.
Аналогично, для второго маятника
2 |
|
|
2 # |
|
(2.47) |
||
|
2 2#2 2 2#2 |
1 #2 |
|||||
Уравнения (2.46) и (2.47) преобразуем к виду |
|
|
|||||
|
|
#1 012 #1 ;12 #1 #2 , |
|
(2.48) |
|||
2 |
|
2 |
#1 , |
|
|||
|
|
|
|||||
|
|
#2 02#2 ;2 #2 |
|
|
|||
где 01 |
1 |
и 02 |
2 |
— собственные частоты каж- |
|||
дого маятника (именно с такой частотой совершал бы гармонические колебания каждый из маятников, если бы не было связи
между ними), ;12 2 1 12, ;22 2 2 22 — коэффициенты, описывающие взаимодействие маятников, обусловленное пружи-
ной.
В общем случае, как мы увидим позднее, колебания маятников #1 и #2 не являются гармоническими. Однако попробуем подобрать такие начальные условия, при которых оба маятника колеблются с одной и той же частотой, совершая гармонические колебания. Рассмотрим для простоты случай одинаковых осцилляторов 01 02 0 и ;1 ;2 ;. Тогда мы

436 |
|
Колебания в линейных системах |
[ Гл. 2 |
||
имеем из (2.48): |
|
|
|||
|
|
#1 02#1 ;2 #1 #2 , |
(2.49) |
||
|
|
2 |
2 # |
||
|
|
|
|||
|
|
#2 0#2 ; 2 #1 |
|
||
|
Легко сообразить, что если, отклонив одинаковые маятники |
||||
на один и тот же угол в одну сторону, отпустить их (рис. 2.12), то |
|||||
пружина в процессе колебаний остается недеформированной (как |
|||||
и в положении равновесия), т. е. не оказывает никакого влияния |
|||||
O1 |
O2 |
на колебания маятников. Каждый из них будет |
|||
колебаться с |
одной и той же частотой |
0 и |
|||
|
|
||||
|
|
# #1 #2 #0 0 (где #0 |
— на- |
||
|
k |
|
|
чальный угол отклонения). |
системы |
уравне- |
|||||||
|
|
|
|
То же самое ясно и из |
|||||||||
|
|
|
|
ний (2.49): при #1 #2 # правые части |
|||||||||
m1 |
m2 |
|
уравнений (2.49) обращаются в нуль и для #1 и |
||||||||||
|
#2 имеем тождественные уравнения |
|
|
||||||||||
|
|
|
|
|
|
||||||||
Рис. 2.12 |
|
|
|
|
2 |
|
0, |
|
2 |
|
|
||
|
|
|
|
|
#1 0#1 |
#2 0#2 0 |
|
||||||
Решение, как мы знаем, — гармоническое колебание часто- |
|||||||||||||
ты 0: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
#1 #2 0 |
|
|
|||||||
Можно угадать и еще один возможный тип колебаний в си- |
|||||||||||||
стеме, приводящий к простому гармоническому колебанию каж- |
|||||||||||||
дого |
из |
маятников |
с одной |
и |
той |
O1 |
O2 |
O1 |
O2 |
||||
же частотой. Отклонив маятники на |
|||||||||||||
один и тот же угол в противополож- |
|
|
|
|
|||||||||
ные стороны, отпустим их (рис. 2.13). |
k |
|
|
|
|||||||||
Ясно, |
что |
одинаковые |
маятни- |
|
|
|
|
||||||
ки |
будут |
качаться |
таким |
обра- |
|
|
|
|
|||||
зом, |
что |
в |
любой момент |
времени |
1 |
2 |
|
|
|||||
m1 |
m2 |
m1 m2 |
|||||||||||
#1 #2 . Проверим наше пред- |
|||||||||||||
положение, обратившись вновь к си- |
à |
Рис. 2.13 |
|
á |
|||||||||
стеме (2.49). |
|
|
|
|
|
|
|
|
|
||||
Подставляя в правую часть |
первого из уравнений # |
||||||||||||
#1 , получим |
|
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
|
|
2 |
2#1 |
|
|
|
|
|
|
|
|
#1 0#1 ; |
|
|
|
||||||
Аналогично, в правую часть второго из уравнений (2.49) подста- |
|||||||||||||
вим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#1 #2 |
|
|
|
|||||
Мы получаем систему двух независимых уравнений:
#1 02 ;2 #1 |
0, |
|
2 |
2 # |
(2.50) |
#2 0 ; |
2 0 |
|

2.5 ] Связанные осцилляторы 437
Из системы (2.50) следует, что в рассматриваемом случае каждый из двух связанных осцилляторов совершает гармонические колебания с частотой
2 |
2 |
0 |
; |
(которая оказалась отличной от собственной частоты колебаний0 каждого из маятников).
Найденные нами типы колебаний связанных осцилляторов называются нормальными колебаниями или нормальными модами, или просто модами.
Итак, первый нормальный тип колебаний (или первая мода): оба маятника совершают гармонические колебания с частотой1 0, имеют одну и ту же амплитуду и начальную фазу, т. е.
#11 1 1 1 |
, |
(2.51) |
|
#12 1 1 1 , |
|||
|
|||
причем 1 1.
Второй тип колебаний (вторая мода): оба маятника соверша-
ют гармонические колебания с частотой |
2 2 |
, причем |
2 |
0 ; |
|
отклонения от положения равновесия в любой момент времени противоположны:
#21 2 2 2 , |
(2.52) |
|
#22 2 2 2 , |
||
|
где 2 2.
Итак, каждая мода имеет свою собственную характерную частоту ( 1 0 для первой моды и 2 02 >2 для второй
моды) и свою характерную форму, т. е. взаимное расположение колеблющихся осцилляторов в процессе колебаний.
А каков характер колебаний связанных осцилляторов в са-
мом общем случае?
Можно показать, что в общем случае колебание системы представляет собой суперпозицию нормальных типов (мод), а
именно
#1 1 1 1 2 2 2 , |
(2.53) |
|
#2 1 1 2 2 2 2 . |
||
|
||
Из шести констант ( 1, 2, 1, 2, 1, 2) две, как мы |
||
знаем, не являются независимыми: |
|
|
1 1 и 2 2 |
|
|
Прочие же константы — 1, 2, 1 и 2, определяются начальными условиями: начальными углами отклонений маятников и их начальными скоростями.
438 |
Колебания в линейных системах |
[ Гл. 2 |
|
Напомним, что 1 и 2 — это найденные нами частоты соб- |
|
ственных мод, т. е. частоты гармонических колебаний, которые можно возбудить в системе с помощью определенных начальных условий, о которых говорилось ранее.
При произвольных же начальных условиях, как следует из (2.53), колебания осцилляторов не являются гармоническими (они представляют собой суперпозицию двух гармонических колебаний разных частот 1 и 2).
Для проверки справедливости нашего утверждения достаточно подставить функции #1 и #2 в уравнения (2.49) и убедиться в том, что уравнения обращаются в тождество при любых 1, 2, 1, 2.
2.6. Вынужденные колебания гармонического осциллятора (гармоническая внешняя сила)
Ранее мы изучали свободные колебания системы, выведенной из положения равновесия и предоставленной после этого самой себе. Рассмотрим теперь колебательную систему, на которую действует внешняя сила, меняющаяся во времени по гармониче-
скому закону. Колебания, происходящие под действием внешней силы, называют вынужденными.
Рассмотрим пружинный маятник (см. рис. 2.3): на тело массы, кроме упругой силы 7упр (это — внутренняя сила в колебательной системе), действует внешняя сила 7 70 . Второй закон Ньютона имеет вид 70 , и мы приходим к уравнению
2 |
(2.54) |
0 0 , |
где 0 70 , 0 .
При наличии вязкого трения, пропорционального скорости,
|
|
(t) |
|
вместо (2.54) получаем |
|
|
|
|
|
|
|
||
|
|
~ |
|
2Æ 02 0 |
(2.55) |
|
|
|
|
||||
|
|
|
|
|
||
|
L |
|
|
R |
На рис. 2.14 колебательная система дру- |
|
|
|
|
гой физической природы: электрический кон- |
|||
|
|
|
|
|
||
|
|
|
|
|
||
|
C |
|
|
|
тур, содержащий катушку индуктивности +, |
|
|
|
|
|
|||
|
|
|
|
|
конденсатор емкости % и омическое сопро- |
|
|
|
|
|
|
||
|
|
|
|
|
тивление . На этот раз контур |
подклю- |
Рис. 2.14 |
чен к внешней ЭДС, меняющейся по закону |
|
0 . Закон Ома для замкнутой цепи, изображенной на рисунке, имеет вид
;5 : + +

2.6 ] |
Вынужденные колебания гармонического осциллятора |
439 |
По сравнению с (2.24) в последнем уравнении к ЭДС индукции + , возникающей в катушке при изменении в ней тока, добавляется внешняя ЭДС . Вновь учитывая, что : /, приходим к уравнению
/ 2Æ/ 02/ 0 , |
(2.56) |
где 0 0+ и по-прежнему Æ 2+ и 0 1 +% . Получено уравнение, математически тождественное урав-
нению (2.55). Для идеального контура (пренебрегая омическим сопротивлением) вместо (2.56) имеем уравнение, аналогичное (2.54):
2 |
(2.57) |
/ 0/ 0 |
Как и ранее, независимо от физической природы осциллятора, будем обозначать искомую переменную через 9 .
Уравнение, описывающее процесс вынужденных колебаний осциллятора, находящегося под действием гармонической внешней силы, имеет вид
9 2Æ9 029 0 |
(2.58) |
Вдальнейшем удобно, введя вместо константы 0 константу
0 02, записать уравнение вынужденных колебаний (2.60) в виде
9 2Æ9 2 |
2 |
|
(2.59) |
0 |
9 0 |
|
Фактически такая замена означает, что мы переходим к изучению колебаний величины 9, размерность которой совпадает
сразмерностью «внешней силы» .
Вчастности, если речь идет о колебательном контуре, под-
ключенном к внешней ЭДС 0 , то в уравнении (2.59) 9 есть напряжение на конденсаторе. Если исследуются вынужденные колебания пружинного маятника, на который действует внешняя гармоническая сила 7 70 , то 9 в (2.59) — это величина , т. е. изменение упругой силы при колебаниях тела на пружине. (Предоставляем убедиться в этом читателю.)
В теории дифференциальных уравнений доказывается, что общее решение уравнения (2.59), которое математики называют неоднородным, представляет собой сумму общего решения однородного уравнения (2.27) и некоторого «частного» решения неоднородного уравнения (2.58):
9 90 91
Общее решение однородного уравнения (2.27) (т. е. уравнения с нулевой правой частью) уже известно. Это решение
есть не что иное, как процесс свободных колебаний осциллятора.

440 Колебания в линейных системах [ Гл. 2
В зависимости от соотношения параметров Æ и 0, оно имеет вид либо (2.28) при Æ ' 0, либо (2.44) при Æ & 0. Характер колебательного процесса 90 зависит от двух произвольных постоянных. Эти постоянные определяются начальными условиями, т. е. способом, которым возбуждаются свободные колебания (начальным отклонением осциллятора от положения равновесия и его начальной скоростью).
Но в любом случае, при наличии даже как угодно малого затухания (а в реальном осцилляторе затухание всегда имеет место) свободные колебания постепенно затухают и соответствующее решение 90 стремится к нулю. Рано или поздно практически остается лишь второе слагаемое 9 91 . Именно это частное решение неоднородного уравнения и называют «вынужденными колебаниями», которые уже не зависят от начальных условий и определяются лишь внешней силой (ее амплитудой и частотой).
Перейдем к комплексной записи: наряду с уравнением
|
2 |
2 |
|
|
(2.60) |
91 2Æ91 091 0 |
|||||
рассмотрим уравнение |
|
|
|
|
|
|
2 |
2 |
|
|
(2.61) |
92 2Æ9 |
2 092 0 , |
||||
а также уравнение |
|
|
|
|
|
2Æ 2 |
2 |
# |
|
(2.62) |
|
|
0 0D |
|
|
||
Заметим, что правая часть уравнения (2.62) является линейной комбинацией правых частей (2.60) и (2.61): D#
.
Очевидно поэтому, что и решение (2.62) — функция — является аналогичной линейной комбинацией решений 91 и
92 :
91 92
Это легко проверить, домножив левую и правую части (2.61) на мнимую единицу и сложив после этого левые и правые части (2.60) и (2.61), учтя при этом, что 91 92 и
91 92 .
Из сказанного ясно, что если будет найдено комплексное решение уравнения (2.62), то искомое действительное решение — реальный процесс вынужденных колебаний 91 — есть просто реальная часть комплексной функции
91 Re |
(2.63) |
