
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
1.6 ] |
Векторные колебания. Фигуры Лиссажу |
411 |
мумы промодулированы «огибающей» — функцией %0 , спектральная ширина которой определяется длительностью сигнала 70 : 0 2$ >. Функция % имеет вид, показанный на рис. 1.28 б (функция %0 изображена на рисунке штриховой линией).
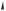
 S
S
à
3 0 2 0 0 0 |
0 2 0 3 0 |
2 |
|
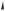 C
C
á
 C0(
C0(
0 |
0 |
2 0 |
3 0 |
2 |
|
|
|
Рис. 1.28
При ! высота спектральных максимумов стремится к бесконечности, а их ширина к нулю: мы получаем «частокол» Æ-функций.
1.6. Векторные колебания. Фигуры Лиссажу
Обратим внимание на формулу (1.6) — правило, по которому мы складываем колебания 91 и 92 . Это правило сложения скалярных величин, т. е. в каждый момент времени мы просто алгебраически складываем две скалярные величины. Мы пользовались графическим изображением колебаний (в виде векторов) лишь для того, чтобы облегчить себе задачу сложения двух скалярных меняющихся во времени величин 91 и 92.
Теперь мы будем говорить о другой проблеме. Представим себе, что колеблющейся величиной является вектор; например, колеблется вектор напряженности электрического поля в данной точке пространства, или вектор магнитного поля, или какая-либо другая векторная величина. При этом в процессе колебаний может изменяться не только модуль вектора, но и его направление


1.6 ] Векторные колебания. Фигуры Лиссажу 413
При 2 1 $, 3$, 5$, ... получаем
2
1
Этот случай показан на рис. 1.29 г.
И в том, и в другом случае вектор S в процессе колебаний
не меняет своей ориентации в пространстве. Такие колебания называются линейно-поляризованными.
Главные оси эллипса совпадают с осями , , если
1)2 1 $ 2 2$ ( 1, 2, ), либо
2)2 1 3$ 2 2$ 1, 2, .
В обоих случаях уравнение эллипса имеет вид (рис. 1.29 в):
2 |
|
2 |
|
|
|
2 |
|
|
|
1 |
(1.60) |
2 |
|||||
1 |
|
2 |
|
|
|
Однако движение конца |
суммарного вектора |
по эллип- |
|||
су (1.60) в случаях 1 и 2 различны. (Вопрос для читателя: в чем состоит это различие?)
Более сложной оказывается траектория движения конца суммарного вектора , если частоты двух взаимно перпендикулярных колебаний не равны. В частности, траектория оказывается замкнутой, если частоты складываемых колебаний относятся как целые числа:
9 |
1 1 , 9 2 2 , (1.61) |
т. е. 1 |
2 . Действительно, промежуток времени |
2$ содержит как целое число периодов колебания 9 , так и целое число периодов колебания 9 , т. е. значения 9 и 9 повторяются через интервал времени 12 — конец вектора попадает в ту же точку на плоскостичерез интервал времени .
m 1 |
, 0 |
m 1 |
, |
m 2 |
, |
m 2 |
, 3 |
n 2 |
|
n 2 |
2 |
n 3 |
4 |
n 3 |
8 |
2A2 |
|
|
|
|
|
|
|

 2A1
2A1
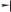
Рис. 1.30
Замкнутая траектория, которую описывает конец суммарного вектора S, называется фигурой Лиссажу. На рис. 1.30 приведены
примеры фигур Лиссажу для некоторых значений 1 2 и
2 1.
414 Кинематика колебаний [ Гл. 1
Фигуры Лиссажу можно наблюдать на экране осциллографа, подавая на горизонтальный вход осциллографа (т. е. на пластины конденсатора, создающего горизонтальное
|
|
|
y |
|
|
|
|
|
|
электрическое поле) напряжение, меняюще- |
|
|
|
|
|||||||||
|
|
|
|
|
|
m |
|
|
еся по закону 1 1 , а |
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
на пластины конденсатора, создающие вер- |
|
|
|
|
|
|
|
|
|
|
|
тикальное электрическое поле, напряжение |
|
n |
|
|
|
|
|
|
|
x |
|||
|
|
|
|
|
|
|
|
|
|
2 2 . |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Электроны, пролетающие между обклад- |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 1.31 |
|
|
ками |
этих конденсаторов навстречу чита- |
|||||
|
|
|
|
телю |
(рис. 1.31), отклоняются суммарным |
||||||
|
|
|
|
|
|
|
|
|
|
||
электрическим полем 1 2 , оставляя на экране осциллографа след, представляющий собой фигуру Лиссажу (например, одну из фигур, изображенных на рис. 1.30).
Задачи
1.Нарисуйте графики ( (осциллограммы) следующих гармонических колебаний: ( 2 100 , ( 5 50 3 , ( 100
2 .
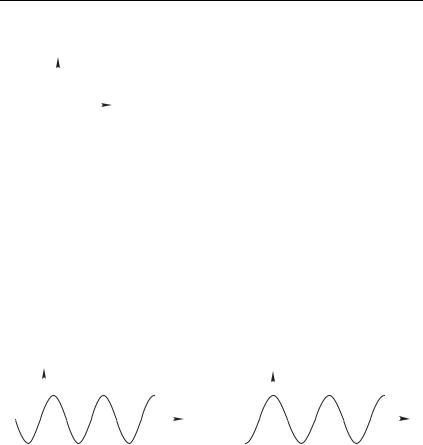
2.Для осциллограмм, изображенных на рис. 1.32, найдите циклическую частоту и начальную фазу гармонических колебаний. Напишите уравнение ( соответствующих гармонических колебаний.
a |
S |
|
|
|
|
a |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
a/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
t, 10 3ñ |
|
|
0 |
0,5 |
t, 10 2ñ |
|||||
|
|
|
à |
|
|
|
|
|
á |
|
|
|
|
Рис. 1.32
3. Найти разность фаз двух колебаний одинаковой частоты и амплитуды, если амплитуда суммарного колебания равна: а) амплитуде слагаемых колеба-
ний; б) в 2 раз больше амплитуды слагаемых колебаний.
4.При сложении трех гармонических колебаний одинаковой частоты и амплитуды оказалось, что суммарное колебание синфазно (т. е. совпадает по фазе) с одним из слагаемых, а его амплитуда вдвое больше амплитуд слагаемых колебаний. Найти разность фаз слагаемых колебаний.
5.Используя графическое изображение, найти сумму B гармонических колебаний одинаковой частоты и амплитуды, фазы которых составляют арифметическую прогрессию: Æ 0, 1, B 1 .
6.Выразить начальную фазу суммарного колебания, изображенного на рис. 1.3, через амплитуды и фазы слагаемых колебаний.
7.Докажите, что точка , изображающая состояние системы на фазовой плоскости, движется с течением времени по часовой стрелке (рис. 1.5 а).
8.Докажите, что семейство фазовых траекторий на рис. 1.5 а описывает гармонические колебания одной и той же частоты . Определите величину .
1.7 ] |
Задачи |
415 |
|
9. Чем отличаются гармонические колебания, отвечающие фазовым траек- |
|
ториям на рис. 1.5 б и в. Найти отношение амплитуд и частот колебаний на этих траекториях.
10. Изображающие точки 1, 2 и 3 находятся в момент времени 0 на прямой : (рис. 1.5 б). Через время точка 2 находится на прямой :. Найти положение точек 1 и 3.
11. Нарисуйте графики (осциллограммы) следующих модулированных колебаний:
а) ( 0 0 , где 0 при, 0; б) ( 0 1 0 при G 1;
в) ( 0 0 2 .
12.Найдите результат сложения гармонических колебаний с близкими
частотами и , амплитуды которых 1 и 2 отличаются. Каково максимальное и минимальное значение квадрата амплитуды (интенсивности) суммарного колебания?
13.При сложении гармонических колебаний с близкими частотами интенсивность суммарного колебания изменяется вдвое. Каково отношение интенсивностей слагаемых колебаний?


418 |
|
Колебания в линейных системах |
|
|
|
[ Гл. 2 |
|||||
(в предыдущих примерах мы полагали, что отсутствуют силы |
|||||||||||
трения и сопротивления воздуха при движении). |
|
|
|
|
|||||||
|
Согласно закону Ома для замкнутой цепи сумма падений на- |
||||||||||
пряжения на всех участках цепи равна сумме ЭДС. Падение на- |
|||||||||||
пряжения — разность потенциалов между обкладками конденса- |
|||||||||||
|
|
тора, равна / %, а ЭДС индукции в |
катушке |
||||||||
|
|
инд + |
|
|
, где : — сила тока. |
|
, сле- |
||||
|
|
Итак: / % + |
. Но : |
|
|||||||
|
L C |
довательно, |
|
|
|
2/ |
2 /; таким образом |
||||
|
|
+/ / % 0, или |
|
|
|
|
|
|
|||
|
|
2 |
|
|
0, |
где |
0 |
1 |
|
|
(2.8) |
Рис. 2.4 |
/ 0/ |
; |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Снова получаем уравнение того же вида, что и (2.3), (2.5), |
||||||||||
(2.7). |
|
|
|
|
|
|
|
|
|
|
|
|
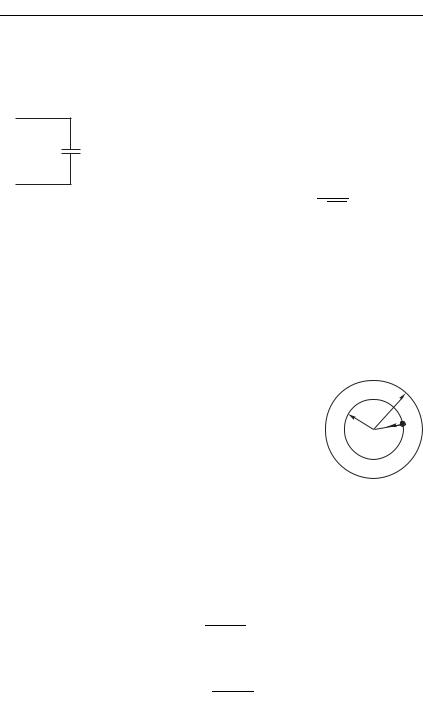
5. Электрон в атоме Томсона. Рассмотрим модель ато- |
||||||||||
ма Томсона, предложенную в 1903 г. Дж.Дж. Томсоном (1856– |
|||||||||||
1940) — до открытия Э. Резерфорда (1871–1937) в 1911 г. — по- |
|||||||||||
ложительно заряженное шарообразное «облако» (его размер , |
|||||||||||
согласно Томсону, определяет размер атома), в котором под |
|||||||||||
действием кулоновской силы двигается отрицательно заряжен- |
|||||||||||
ный, «точечный» электрон. Атом электрически нейтрален, т. е. |
|||||||||||
положительный заряд облака D равен по абсолютной величине |
|||||||||||
отрицательному заряду электрона. |
|
|
|
|
|
|
|||||
|
При смещении относительно центра облака |
|
|
|
R |
||||||
на электрон действует сила , направленная |
|
|
|
||||||||
|
|
|
|
||||||||
к центру и возвращающая электрон к положе- |
|
r |
|
e |
|||||||
нию равновесия (рис. 2.5). |
|
|
|
|
|
|
|
F |
|||
|
|
|
|
|
|
|
O |
||||
|
Эта сила равна D , где — напря- |
|
|
|
|
||||||
женность электрического поля, созданного об- |
|
|
|
|
|||||||
лаком положительного заряда на расстоянии |
|
|
|
|
|||||||
от |
его центра. Применим теорему |
Гаусса к |
|
Рис. 2.5 |
|||||||
сфере радиуса : поток вектора через по- |
|
||||||||||
|
|
|
|
||||||||
верхность этой сферы равен 1<0 /, где / — полный заряд, |
|||||||||||
находящийся внутри сферы. Полагая, что заряд облака D рас- |
|||||||||||
пределен равномерно, получим / 3D. Теорема Гаусса дает: |
|||||||||||
- 4$ 2 1<0 3D, или - D 4$<0 3 . Если — |
|||||||||||
радиус-вектор, проведенный из центра в точку, где находится |
|||||||||||
электрон, то сила F есть |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
<2 |
|
|
|
|
|
|
|
|
|
400 |
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
Второй закон Ньютона (уравнение движения электрона) име- |
||||||||||
ет вид |
|
|
|
<2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.9) |
||
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
400 |
|
|
|
|
|
||

420 |
Колебания в линейных системах |
[ Гл. 2 |
Итак, согласно (2.11), вторая производная от смещения осциллятора из положения равновесия 9 пропорциональна (и противоположна по знаку) величине смещения 9. Какова же зависимость 9 , удовлетворяющая уравнению (2.11)?
2.2. Свободные колебания гармонического осциллятора
Легко убедиться, что решением уравнения (2.11) является гармоническое колебание (поэтому-то система, описываемая этим уравнением, и называется гармоническим осциллятором).
Действительно, дифференцируя функцию
9 |
(2.12) |
дважды, находим:
9 , 9 2 (2.13)
Подставляя (2.12) и (2.13) в (2.11), убеждаемся, что уравнение обращается в тождество, причем значения и могут быть любыми. Другими словами, (2.12) — это множество решений, или, как говорят математики, общее решение, содержащее две произвольные постоянные. Итак, любая из описанных нами физических систем, а также множество других систем, подчиняющихся уравнению (2.11), будучи выведенными из положения
равновесия, совершают гармонические колебания. Эти колебания называются свободными, поскольку достаточно вывести систему
из положения равновесия — и колебания далее происходят «сами по себе», без какого-либо внешнего воздействия.
Произвольные постоянные и — амплитуда и начальная фаза — определяются начальными условиями, тем, как именно система выводится из положения равновесия. Например, маятник можно отклонить от положения равновесия на некоторый угол
#0 и затем отпустить. Этот момент (когда маятник отпускают) и есть начальный момент времени 0. Мы имеем в этом случае начальные условия: # #0 при 0; это условие записывают в виде
# 0 #0 |
(2.14) |
Одного условия (2.14) недостаточно для определения двух постоянных и . Второе условие — задание начальной скорости. В нашем примере (маятник, отклонив, отпускают) мы имеем
# 0 0 |
(2.15) |
Имея общее решение |
|
# |
(2.16) |

 x
x 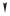 m
m