
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
5.2 ] Упругие волны в жидкостях и газах 491
костей можно полагать, что процесс сжатия и разряжения данной массы жидкости или газа (заключенного на участке трубы
) происходит без обмена теплом с соседними участками, т. е. адиабатически. В этом случае плотность и температура связаны уравнением адиабаты (в частности, для идеального газа
0 3 30 1, где 5 ) и поэтому давление можно
считать функцией лишь одного параметра — плотности, т. е.
8 8 3 Тогда, при малых изменениях плотности, можно
записать |
|
& |
|
(5.10) |
|
8 |
3 |
||
|
|
|||
|
% |
|
|
|
Производная |
берется в точке 3 30, 80 8 30 Вели- |
|||
чина 8 называется акустическим давлением, это отклонение давления от равновесного значения при распространении акустической волны.
Свяжем теперь изменение плотности с изменением давления,
используя соотношение 30 3 20 2 3020 ( — фиксированная масса газа между сечениями и ). Полу-
чаем |
" < |
|
% |
% |
|||
|
|
||||||
|
|
|
|
|
|
||
|
"0 |
%0 % %0 |
|||||
Таким образом, формула (5.10) приобретает вид |
|||||||
|
8 30 |
& |
< |
(5.11) |
|||
|
% |
||||||
Как видно из (5.11), роль модуля упругости в жидкости и |
|||||||
газе играет величина - 3 |
|
, причем 8 ; (знак « » |
|||||
указывает, что увеличение давления ( 8 & 0) приводит к сжатию (< & 0)). Подставляя (5.11) в (5.9), приходим к волновому уравнению
2H |
1 |
|
|
2H , |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 & % 2 |
|
||||||||||
в котором величина |
представляет собой квадрат скорости |
||||||||||
распространения звуковой волны |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
(5.12) |
||||||
|
% |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
В качестве примера рассмотрим идеальный газ: 8 3 . Как |
|||||||||||
показано Лапласом, скорость звука в таком газе |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
, &0 |
|
|
5 0 , |
(5.13) |
|||||||
|
|
%0 |
|
|
|
||||||
|
|
|
|
|
|
|
|||||
где 5 .
Формула (5.13) имеет ясный физический смысл: передача возмущений в звуковой волне в газе осуществляется за счет теп-

5.3 ] Плотность и поток энергии в упругой волне. Вектор Умова |
493 |
|||||||||
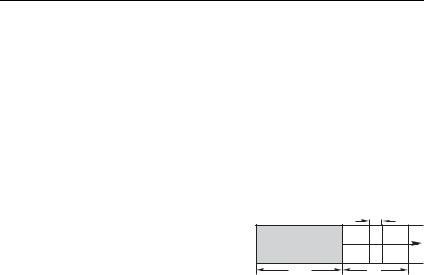
левая граница участка (сечение 1 на рис. 5.5) неподвижна, |
||||||||||
а правая смещается на расстояние A < Работа внешней |
||||||||||
силы (упругой силы, действующей на выделенный участок со |
||||||||||
стороны прилегающего к нему участка справа) при растяжении |
||||||||||
участка на величину A есть |
|
|
|
|
|
|||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Величина |
деформации < |
и, |
соответственно, |
упругая |
сила |
||||
-<9 меняются в процессе деформации. При смещении сече- |
||||||||||
ния 2 (на рис. 5.5) на величину |
деформация участка стержня |
|||||||||
меняется |
на величину |
, |
причем |
|
|
d |
|
|||
|
|
. Упругая |
сила |
|
при |
1 |
2 |
3 |
||
заданной величине деформации, со- |
|
|
|
F |
||||||
гласно закону Гука, есть 9-<, |
|
|
|
|
||||||
а ее работа при смещении сечения 2 |
z |
|
|
|
||||||
на |
равна |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
9 << |
|
|
Рис. 5.5 |
|
|
||
|
Полная работа (при смещении правой границы на величину |
|||||||||
A, которой соответствует конечная величина деформации <), есть |
||||||||||
6 |
) |
2 |
|
*02 2 , |
9 -< 9 *02 |
2 |
|||
00
где 2 — объем кусочка стержня 2 9 Работа внешних сил равна запасенной участком стержня по-
тенциальной (упругой) энергии. На единицу объема приходится
энергия |
*02 |
|
|
)п |
, |
(5.15) |
|
|
2 |
|
|
которая называется объемной плотностью потенциальной энергии. Общая плотность энергии (кинетическая плюс потенциальная) есть
) |
1 |
342 -<2 |
(5.16) |
|
2 |
||||
|
|
|
В бегущей волне A плотность энергии в данный момент времени равна нулю там, где максимально смещение A, так как при этом 4 A 0 и < -A 0 (см. (5.7) и (5.8)). Плотность энергии максимальна там, где и деформация <, и скорость 4 максимальны (причем < и 4 максимальны в каждый момент времени в одном и том же сечении , что ясно из тех же соотношений (5.7) и (5.8)). В бегущей гармонической волне A и A нулевым значениям

494 Упругие волны [ Гл. 5
смещения A соответствует максимум A и, следовательно, максимумы 4 и <, а значит и максимум плотности энергии.
Поток энергии. Вектор Умова. Найдем изменение энергии в куске стержня между сечениями 1 и 2 при распространении звуковой волны (рис. 5.3). Слева (в сечении 1) действует сила1 ;19. Напомним, что ; положительно, если правая от сечения часть стержня тянет левую вправо, в положительном направлении оси , при этом часть стержня, находящаяся левее сечения 1, действует на выделенный участок с силой, направленной влево, т. е. должна быть отрицательной. Справа (в сечении 2) действует внешняя сила 2 ;29 (при ;2 положительном2 & 0). Работа сил 1 и 2 за время равна
141 242 ;141 ;242 9
Эта работа равна изменению энергии |
куска стержня за |
|
время |
|
|
> |
;1419 ;2429 |
(5.17) |
|
|
|
Введем плотность потока энергии, / ;4. Тогда /9 —
поток энергии через площадку 9 и формула (5.17) выглядит так:
> |
/1 /2 9 |
(5.18) |
|
|
|
Равенству (5.18) можно дать следующее толкование: увеличение энергии в куске стержня равно разности между потоком энергии /1 ;1419, проникшем в кусок стержня через сечение 1 и потоком /2 ;2429, вытекшим из куска стержня через сечение 2. Векторная величина
;4 , |
(5.19) |
где — единичный вектор, направление которого совпадает с
направлением распространения бегущей волны (осью ), называется вектором потока энергии. Этот вектор впервые введен рус-
ским ученым Н.А. Умовым (1846–1915), и его называют также вектором Умова. Это аналог введенного в предыдущем разделе
вектора Пойтинга — потока электромагнитной энергии. Аналогичным образом, поток энергии в акустической волне
в газе или жидкости
84 |
(5.20) |
Среднюю величину потока энергии, переносимого акустиче-
ской волной в единицу времени через единичную площадку (в направлении нормали) называют интенсивностью или силой звука. Для гармонической волны (A , , —
амплитуда смещений частиц) находим
4 H |
; |
< H , |
|
|
|
5.3 ] |
Плотность и поток энергии в упругой волне. Вектор Умова |
495 |
где — волновое число. Соответствующие волны напряжений ; , или акустических давлений 8 можно найти с помощью (5.2) и (5.11):
; -< * ; |
8 3 & |
|
|
% |
|
Для интенсивности (силы звука) в твердых телах получаем
|
|
|
2 2* |
|
|
|
1 |
2 2 3- |
1 |
2 23 |
|
: |
|
|
|
2 |
|||||||
;4 |
|||||||||||
|
2 |
|
|||||||||
|
2 |
|
|||||||||
Учитывая, что , интенсивность звука в жидкостях и газах есть
|
|
|
1 |
|
2 23 & |
1 |
|
2 23 |
||
: 84 |
|
|
||||||||
2 |
% |
|
2 |
|
||||||
|
|
|
|
|
|
|||||
Важно обратить внимание, что интенсивность пропорциональна
квадрату амплитуды смещений.
Из полученных соотношений легко найти связь между амплитудой акустического давления и интенсивностью
80 23 : |
(5.21) |
Интересно отметить, что порог слышимости (минимальная слышимая интенсивность звука) :0 10 12 Вт/м2 близок к предельно возможному: кинетическая энергия барабанной перепонки, колеблющейся под действием теплового движения молекул воздуха примерно того же порядка, что и под действием пороговой акустической волны. Диапазон регистрируемых ухом человека интенсивностей огромен: «болевой порог» составляет примерно 1012:0 (такова сила звука на концерте рок-музыки
в первых рядах). В силу столь большого диапазона удобно выражать интенсивность звука в децибеллах (обозначается через *):
* 10 + дБ
+0
Величина 1010:0 составляет * 100 дБ, порог слышимости *0 0, а болевой порог * 120 дБ.
Акустические волны большой интенсивности создают в среде большие перепады давлений. Амплитуда акустического давления80 в волне с : 105 Вт/м2 составляет в воде, согласно (5.21),80 6 атм, а большие градиенты акустического давления, возникающие при распространении ультразвуковых волн, могут
приводить к разрывам жидкости (т. е. к образованию пустот). Это явление называется кавитацией. В приведенном примере
при частоте ультразвука ( 106 Гц ( 5 10 4 м) градиент акустического давления равен 2,40 104 атм/м.
496 |
Упругие волны |
[ Гл. 5 |
5.4. Стержень, закрепленный на концах. Собственные моды колебаний
Рассмотрим бесконечно длинный стержень, по которому бегут две встречные гармонические волны одинаковой частоты и амплитуды:
A1 ; A2 $
Мы по прежнему говорим об упругих продольных волнах. Начальная фаза в волне A2 выбрана так, чтобы в сечении 0 колебания встречных волн происходили в противофазе, т. е. так,
чтобы смещение A A1 A2 частиц стержня в этом сечении в любой момент времени равнялось нулю. Суммарная стоячая
волна A , A1 , A2 , имеет вид
A , 2 |
(5.22) |
Выделим мысленно кусок стержня длины + между сечениями0 и + и подберем частоту встречных волн так, чтобы смещение A в сечении + (также, как в сечении 0) было равным нулю в любой момент времени. Как ясно из (5.22), для этого необходимо, чтобы + 0, т. е. + $ ( — целое число). Так как 2$ , то последнее условие можно записать
в виде |
|
+ |
(5.23) |
|||
|
|
|||||
|
|
|
|
2 |
|
|
Или, поскольку частота и длина волны связаны соотно- |
||||||
шением 2$ , то |
|
|
|
|
|
|
|
|
1, 2, или ( |
(5.24) |
|||
|
|
|
|
2 |
|
|
Используя (5.6), |
можно |
последнее соотношение |
записать |
|||
в виде |
|
|
|
|
|
|
|
|
* 1, 2, |
(5.25) |
|||
|
|
|
|
% |
|
|
|
|
|
|
|
||
Итак, имеется дискретный набор частот , при которых сечения 0 и + остаются неподвижными в любой момент времени (узлы стоячей волны (5.22)). Соответствующие частотамстоячие волны имеют вид (поскольку 2$ $+)
A , 2 |
(5.26) |
|
|
Мы выяснили ранее, что поток энергии в стоячей волне равен тождественно нулю (в любой момент времени) в тех сечениях , где смещение равно нулю. Следовательно, выделенный нами кусок стержня длины + не обменивается энергией с внешними частями, расположенными левее (при ' 0) и правее (при & +).
5.4 ] |
Стержень, закрепленный на концах |
497 |
Если теперь в некоторый момент времени закрепить «намертво» сечения 0 и +, то волновое движение, описываемое формулой (5.26), не изменится, поскольку и до закрепления эти сечения были неподвижны. Можно теперь обрезать внешние по отношению к этому куску участки стержня, стоячая волна на оставшемся куске при этом никак не изменится, кусок стержня будет колебаться в согласии с уравнением (5.26), не отдавая и не получая энергии извне. Разумеется, для возбуждения этого колебания никто не берет бесконечно длинный стержень, возбуждая в нем бегущие встречные волны, а затем обрезая в нужном месте кусок длины +. На самом деле поступают наоборот: берут стержень нужной длины +, закрепленный жестко на концах, а затем возбуждают в нем колебания одной из возможных частот
Функции (5.26) определяют возможные типы продольных упругих волн в стержне с закрепленными концами. Соответствую-
щие частоты этих волн даются формулами (5.24) или (5.25). Гармонические стоячие волны A , называются собственными типами или собственными модами (или просто модами).
Не отдавая энергию в местах закрепления (поскольку поток энергии в этих местах равен нулю), такие колебания могут самоподдерживаться как свободные колебания гармонического
осциллятора без затухания. Мода, отвечающая индексу 1, называется основной.
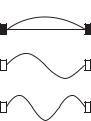
Распределение амплитуды смещений по ко- à ординате :
2 |
á |
|
|
|
|
|
|
|
|
|
|
|
|
|
определяет пространственную структуру раз- |
â |
n 2 |
|
|
ных типов колебаний. Эти распределения для |
|
|
||
|
|
|
|
|
1, 2, 3 показаны на рис. 5.6 а, б, в. |
|
|
|
|
Еще раз обратим внимание на важное об- |
|
|
n 3 |
|
стоятельство: если в бесконечном стержне возможно создать стоячую волну любой часто-
ты , то в стержне конечной длины + с закрепленными концами возможны лишь определенные, дискретные конфигурации стоя-
чих волн с дискретным набором частот , поскольку только такие типы стоячих волн могут удовлетворять граничным условиям A 0 A + 0.
Вывод, к которому мы пришли, носит достаточно общий характер: как только мы пытаемся «запереть» волновое движение в конечной области пространства, тут же возникает дискретность возможных частот, дискретность возможных конфигураций волн и дискретность возможных значений энергии колебаний.

498 Упругие волны [ Гл. 5
Возможным типам стоячих волн смещений A , (5.26)
состветствуют стоячие волны |
скорости смещений 4 , |
||
.A . и деформаций < , .A . Мы получаем |
|
||
4 , 2 , |
|
||
|
|
(5.27) |
|
< , 2 |
|||
|
|||
|
|
|
|
Рассмотрим энергетические превращения при колебаниях стержня.
Впроцессе колебаний происходит обмен между кинетической
ипотенциальной частями полной энергии (последняя, как мы выяснили, остается неизменной). Как видно из формул (5.27),
дважды за период скорость смещений 4 , и деформация стержня < , становятся равными нулю в любом сечении стержня.
Следовательно, дважды за период становится равной нулю кинетическая энергия 4 , 0 при 4 и 3 4 — и в эти моменты времени полная энергия колебаний — это потенциальная энергия упругой деформации:
|
1 |
+ |
|
|
|
|
)п |
|
-<2 |
, |
(5.28) |
||
2 |
|
|||||
|
|
|
|
|||
|
|
0 |
|
|
|
где < 2$+ $+ ( 1 при 4 и
3 4).
Аналогично, дважды за период обращается в нуль потенциальная энергия (< , 0 при 0 и 2). В эти моменты времени энергия колебаний — это кинетическая энергия, равная
|
1 |
+ |
|
|
|
|
)к |
|
342 |
, |
(5.29) |
||
2 |
|
|||||
|
|
|
|
|||
|
|
0 |
|
|
|
где 4 2 $+ Поскольку полная энергия колебаний постоянна, то любую из формул (5.28) или (5.29) можно использовать для подсчета ее конкретного значения. В частности, из (5.29) легко получить
)к 2 2 2 , |
(5.30) |
где 2 — объем стержня, определяется формулой (5.25). Основной тип колебаний имеет наинизшую энергию, поскольку ему соответствует наинизшая частота. Энергия -го типа пропорциональна 2 Формула (5.30) определяет возможные дискретные значения энергии колебаний.

5.5 ] Поведение звука на границе раздела двух сред 499
5.5. Поведение звука на границе раздела двух сред
Рассмотрим плоскую звуковую волну |
|
A1 1 1 , |
(5.31) |
распространяющуюся в однородной среде I в области ' 0 (рис. 5.7). Волна распространяется слева направо, в положительном направлении оси , 1 1 — волновое число, 1 — скорость звука в среде I. Плоскость 0
является границей раздела двух сред. Об- |
1 |
|
I II |
|
|
||||
ласть & 0 занята средой II, скорость звука |
2 |
z |
|||||||
|
|
|
|
|
|
|
|||
в которой 2 1 (напомним, что скорости |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||
1 и 2 зависят от упругих свойств и плот- |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
ности сред (см. (5.6)). |
|
|
|
Рис. 5.7 |
|
|
|||
Что происходит с волной A1 , , падаю- |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
щей на границу раздела? В соответствии с тем, что подсказывает нам опыт, предположим, что возникает волна, прошедшая во вторую среду
A2 , 2 2 , |
(5.32) |
где 2 2, а в первой среде, кроме волны A1 , , бегущей
слева направо и падающей на границу раздела, возникает отраженная волна
A , |
1 |
(5.33) |
|
1 |
1 |
|
|
Обратите внимание на знак « » в аргументе косинуса: отраженная волна бежит справа налево; кроме того, волновое число этой волны то же, что и в падающей волне, так как обе они распространяются в среде I. Суммарная волна в среде I есть
A1 , A |
, 1 1 1 |
(5.34) |
1 |
1 |
|
Наша задача: найти амплитуды отраженной волны |
и вол- |
|
|
1 |
|
ны, прошедшей во вторую среду 2, зная амплитуду падающей |
||
волны 1 Воспользуемся условиями на границе 0 Во-первых, одно
и то же смещение границы A можно выразить как через волновое возмущение (5.34) в первой среде, так и через волновое возмущение (5.32) во второй среде; равенство волновых возму-
щений при 0 есть: |
|
|
|
|
A |
0, A |
0, A |
0, |
(5.35) |
1 |
1 |
2 |
|
|
Во-вторых, упругая сила (на единицу площади), действующая со стороны первой среды на вторую, равна по величине силе, действующей со стороны второй среды на первую:
; |
0, ; |
0, ; |
0, , |
(5.36) |
1 |
1 |
2 |
|
|

500 Упругие волны [ Гл. 5
где ; - .A . . Подставляя выражения (5.33) и (5.34) (при0) в граничное условие (5.35), получаем (сокращая на общий
множитель ) |
|
|
|
(5.37) |
1 |
|
2 |
|
|
1 |
|
|
|
|
Аналогичным образом, дифференцируя функции |
(5.33) |
|||
и (5.34) по и используя граничное условие (5.36), находим (сокращая на )
-1 1 1 1 -2 2 2 |
(5.38) |
Из (5.37) и (5.38) имеем выражения, которые связывают амплитуды отраженной и прошедшей волны с амплитудой падающей волны
1 |
1 , |
1 |
, |
2 |
|
2 |
|
1 |
|
(5.39) |
|||
1 , |
1 , |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
Мы использовали обозначение 5 *2 |
2 |
|
%2 |
*2 |
. |
||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
*1 |
1 |
|
|
|
|
*1 |
|
|
|
|
|
|
|
|
|
|
|
%1 |
|
|
||
Используя выражения для среднего потока энергии / в упругой среде за период колебаний (см. (5.19)), можно найти вели-
чины / |
/1 (коэффициент отражения) и /2/ |
(коэф- |
||||||
1 |
|
|
|
|
|
|
1 |
|
фициент прозрачности): |
2 |
|
|
|
||||
|
|
1 , |
|
4, |
|
|||
|
|
|
|
|
, |
|
|
(5.40) |
|
|
1 , |
1 , 2 |
|||||
|
|
|
|
|
|
|||
5.6. Поперечные волны в струне
Рассмотрим натянутую струну, ось которой совпадает в равновесии с осью . Рассмотрим распространение поперечных упругих волн в струне, причем будем рассматривать смещения, происходящие в плоскости .
Пусть струна выведена из положения равновесия; смещение куска струны (между точками и ) в данный момент
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
времени есть @ , (рис 5.8). Бу- |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z z) |
дем полагать далее, что натяжение |
|||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
струны (равное при равновесии ;) |
|
(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z z) |
столь велико, что при малом сме- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
щении из положения равновесия оно |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
остается практически неизменным и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
равным по прежнему ; в любом се- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z |
|
чении: |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Рис. 5.8 |
; ; ; |
|||||||||||||||||||||||
Напомним, что ; — сила, действующая на единицу площади выделенного участка струны со стороны участков, прилегающих слева и справа.
