
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf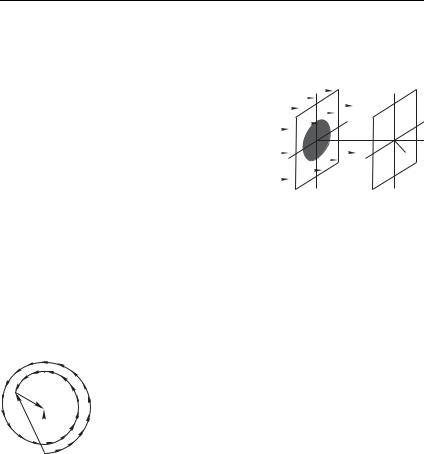
8.7 ] Дифракция Френеля 591
размер отверстия в непрозрачном экране равен радиусу первой зоны Френеля (отверстие освещается плоской волной интенсивности :0)?
Пятно Пуассона. Пусть на пути плоской волны расположен непрозрачный круглый диск (либо круглый шарик). Какова
интенсивность света в точке 6, рас- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
положенной за диском на оси, про- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ходящей через его центр (рис. 8.21)? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если расстояние столь мало, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
выполняются условия геометрической |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
оптики ( 0 1, 0 — радиус |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
диска), то в плоскости наблюдения мы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
получим резкую границу света и тени, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
точка 6 находится как раз посередине |
|
|
|
|
Рис. 8.21 |
|
|||||||||||||||||
круговой области тени и интенсив- |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ность равна нулю. Будем постепенно удалять точку наблюдения |
|||||||||||||||||||||||
от диска. Число зон Френеля, перекрываемых диском, будет |
|||||||||||||||||||||||
постепенно уменьшаться. К чему это приводит? |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Прежде, чем ответить на этот вопрос, напомним, что при |
|||||||||||||||||||||||
отсутствии препятствия на пути волны колебание в точке на- |
|||||||||||||||||||||||
блюдения изображается вектором 0 (т. е. амплитуда колебаний |
|||||||||||||||||||||||
определяется длиной вектора 0), проведенным из начала спира- |
|||||||||||||||||||||||
ли в ее фокус (см. рис. 8.18). Понятно, что это колебание можно |
|||||||||||||||||||||||
|
представить как сумму колебаний, которые со- |
||||||||||||||||||||||
|
здаются сравнительно небольшим количеством |
||||||||||||||||||||||
A |
нескольких первых зон Френеля (вектор |
1 на |
|||||||||||||||||||||
рис. 8.22 изображает вклад трех целых зон |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
A1 |
|
A0 |
плюс примерно треть четвертой зоны — три |
|
|||
|
и одна треть полувитков спирали Френеля) и |
||
|
|
|
колебания, созданного всеми остальными зона- |
|
|
|
ми — их вклад изображается вектором A на |
Рис. 8.22 |
рис. 8.22. Действительно, мы видим, что сумма |
||
|
|
|
векторов 1 и A дает нам вектор 0. |
Если теперь на пути волны установить непрозрачный диск, перекрывающий вклад нескольких первых зон Френеля (например, тех самых трех и одной трети зон), то колебание в точке наблюдения создается теперь лишь оставшимися периферийными зонами, вклад которых изображается вектором A. Мы видим, что если число перекрытых диском зон не слишком велико, так что скручиванием спирали можно пренебречь, то длина вектора A, т. е. амплитуда колебаний в центре тени от диска практически такая же, какая была бы в точке 6 при отсутствии диска.
Из сказанного выше ясно, что совершенно неважно, каков конкретный радиус диска (или шарика). Длина вектора A на рис. 8.22 практически не изменилась бы, если бы диск перекрыл не три с небольшим зоны Френеля, а, скажем, семь с небольшим
592 |
|
|
Дифракция |
|
|
|
[ Гл. 8 |
||
зон или тринадцать с небольшим зон. Важно лишь, чтобы не стало |
|||||||||
проявляться скручивание спирали, о котором мы говорили ранее. |
|||||||||
Яркое пятно, возникающее в центре геометрической тени от |
|||||||||
шарика (или диска), называется пятном Пуассона. Интересно, |
|||||||||
что Пуассон не верил в справедливость волновой теории света и |
|||||||||
привел изложенные нами выше соображения как доказательство |
|||||||||
ее абсурдности. Лишь после этого яркое пятно в центре тени от |
|||||||||
шарика наблюдал экспериментально Араго. |
|
|
|
||||||
8.8. Дифракция Френеля на одномерных структурах |
|
||||||||
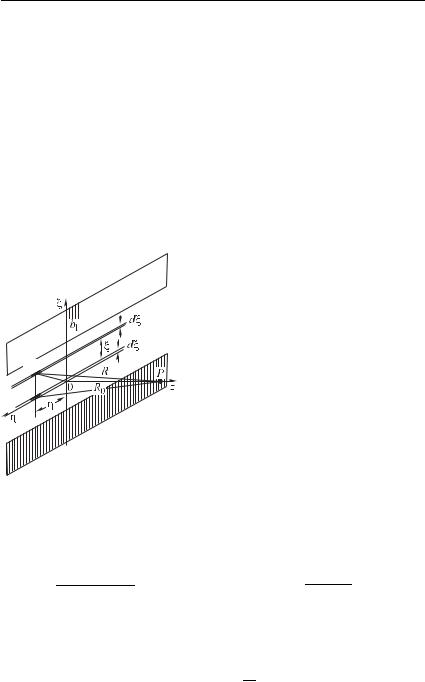
Дифракция на щели. В качестве примера такого рода задач |
|||||||||
рассмотрим дифракцию плоской волны на непрозрачном экране, |
|||||||||
отверстие в котором имеет вид очень длинной щели с прямо- |
|||||||||
линейными краями (рис. 8.23). Края щели параллельны оси @. |
|||||||||
|
|
|
|
Верхний край совпадает с прямой |
|||||
|
|
|
|
0 1, а нижний с 0 2 (ширина |
|||||
|
|
|
|
щели 1 2). Нас интересу- |
|||||
|
|
|
|
ет световое колебание в точке 6, |
|||||
|
|
|
|
расположенной на расстоянии за |
|||||
|
|
|
|
щелью. Рассмотрим вначале коле- |
|||||
|
|
|
|
бание, созданное в точке наблюде- |
|||||
|
|
|
|
ния 6 всеми вторичными источни- |
|||||
d |
|
|
|
ками (элементарными площадками |
|||||
|
|
|
|
;0 |
|
|
), находящимися на |
||
d0 |
|
|
|
оси @. Пусть амплитуда колебаний, |
|||||
|
|
|
|
созданных всеми этими площадка- |
|||||
|
|
|
|
ми (узкой полоской толщины |
) |
||||
|
|
|
|
в точке 6 равна 0 |
(начальную |
||||
|
|
|
|
фазу примем равной нулю). Како- |
|||||
|
|
|
|
во колебание, созданное столь же |
|||||
|
Рис. 8.23 |
|
узкой полоской, параллельной оси |
||||||
|
|
@ и находящейся на расстоянии 0 |
|||||||
|
|
|
|
||||||
от оси @ (см. рис. 8.23)? Сравним вклады двух элементарных |
|||||||||
площадок |
и |
0, одна из которых |
0 |
находится на узкой |
|||||
полоске, совпадающий с осью @, а вторая |
|
— на интересующей |
|||||||
нас полоске на расстоянии 0 от |
0. Сравним расстояния и |
||||||||
0 от |
и |
0 до точки 6: |
|
|
|
|
|
|
|
2 @2 02 42 |
12 ; |
0 2 @2 42 |
|
||||||
|
|
|
2 |
2 |
|
|
|
2 |
|
(это приближение мы уже использовали ранее, см. (8.46)). Из
последних равенств находим разность расстояний 02 2 и разность фаз колебаний в точке 6
|
02 |
(8.53) |
2 |
|
|
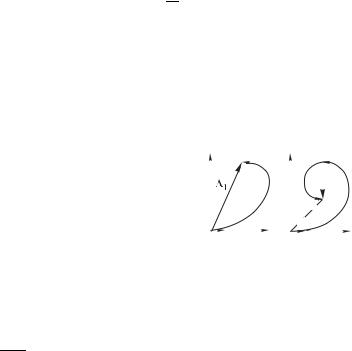
8.8 ] |
Дифракция Френеля на одномерных структурах |
593 |
||
Понятно, что и суммарное колебание, созданное в точке 6 |
||||
полоской |
площадок |
, отстает по фазе на |
величину |
от |
колебания, созданного полоской площадок |
0, находящихся на |
|||
оси @. Итак, колебание от интересующей нас полоски вторичных источников в точке наблюдения 6 можно записать в виде
0 2C 02 |
(8.54) |
Разбив всю щель на такие элементарные полоски, параллельные краям щели, и сложив колебания от всех элементарных полосок, заполняющих щель (от 1 до 2), найдем
/2 |
2C 02 |
|
7 6 0 |
(8.55) |
|
/1 |
|
|
Мы приходим к спирали Корню (см. § 1.3), которая служит для оценки интеграла (8.55).
Последний из изображенных на рис. 8.24 векторов 1 антиколлинеарен первому вектору 0. Он изображает вклад полоски вторичных источников, который противофазен вкладу первой полоски (находящейся на оси @). Мы получаем 2 02 $, откуда находим расстояние от края этой ( -й) полоски до оси @:
0 2$ . Суммарный |
|
|
|
|
|
|
вклад всей полосы (от оси @ до -й по- |
a1 |
|
a1 |
|||
|
||||||
лоски) изображается вектором 1, про- |
|
|||||
веденным из начала первого вектора 0 |
|
|
|
A2 |
||
|
|
a2 |
||||
в конец последнего вектора 1. Будем |
|
|
||||
продолжать наше построение, пристраи- |
a0 |
|
a0 |
|
||
вая на векторной диаграмме вклады по- |
|
|
||||
следовательно расположенных полосок, |
Рис. 8.24 |
Рис. 8.25 |
||||
все далее отстоящих от оси @. Мы полу- |
||||||
|
|
|
|
|
||
чим еще один полувиток (рис. 8.25), причем вектор 2 изображает вклад полоски, отстоящей от точки наблюдения на расстояние(оно больше, чем расстояние от оси @ до точки наблюдения, на длину волны ), поэтому вектора 0 и 2 коллинеарны — разность фаз колебаний 2$. Мы имеем 2 02 2$, от-
куда 0 2 . Вектор 2 изображает суммарный вклад полосы,
лежащей между двумя прямыми 0 01 и 0 02 2 . В данном случае вместо кольцевых зон Френеля мы имеем зоны в виде полос (их называют зонами Шустера по имени англий-
ского физика А. Шустера (1851–1934)).
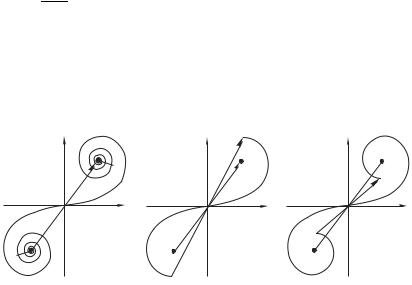
Продолжая дальше построение векторной диаграммы, мы придем к спирали Корню, изображенной на рис. 8.26. Спираль,
очень быстро скручиваясь (благодаря квадратичной зависимости фазы колебаний 2 02 от координаты 0), все ближе при-
594 |
Дифракция |
[ Гл. 8 |
ближается к точке 91, называемой фокусом спирали. Каждый последующий полувиток спирали изображает вклад в суммарное колебание последовательно расположенных зон Шустера, причем-я зона Шустера — это полоса, внешний край которой отстоит от точки наблюдения на расстояние 2 и на расстояние
0 от оси @. Нижняя половина спирали Корню (от нуля до точки 92) описывает вклад вторичных источников (элементарных полосок 0 ), расположенных ниже оси @ (0 ' 0). С ростом ширины щели ( 1 , 2 на рис. 8.23) работают все более мелкие витки спирали Корню, которые все ближе прилегают к фокусам 91 и 92. Вектор 0, соединяющий фокусы спирали, определяет амплитуду колебаний в точке наблюдения при отсутствии препятствия.
|
A S1 |
S1 |
A0 |
S1 |
|
|
|
|
|
|
A |
0 |
0 |
0 |
S2 |
S2 |
S2 |
Рис. 8.26 |
Рис. 8.27 |
Рис. 8.28 |
Очевидно, амплитуда колебаний в точке 6 близка к максимальной, если открыты две зоны Шустера (т. е. «работает» один полувиток верхней половины спирали и один полувиток нижней половины, рис. 8.27). Амплитуда колебаний (длина вектора A) при этом больше, чем амплитуда колебаний 0 при отсутствии препятствия. Соответствующая ширина щели равна при этом2 . Если размер щели увеличить таким образом, что
2 2 (так, что на верхней и нижней полуспирали начинают «работать» полувитки вторых зон Шустера, рис. 8.28), то амплитуда колебаний в точке наблюдения уменьшается: длина вектора A на рис. 8.28 меньше, чем 0.
Дифракция на краю экрана. С помощью спирали Корню можно качественно исследовать картину дифракции плоской волны на полубесконечном экране (непрозрачный экран с прямолинейным краем перегораживает нижнюю полуплоскость 0 ' 0, рис. 8.29). Согласно законам геометрической оптики в плоскости наблюдения мы должны были бы иметь распределение интенсивности, показанное на рис. 8.29 штриховой линией: интенсивность равна нулю в области тени ( ' 0) и равна :0 при & 0.
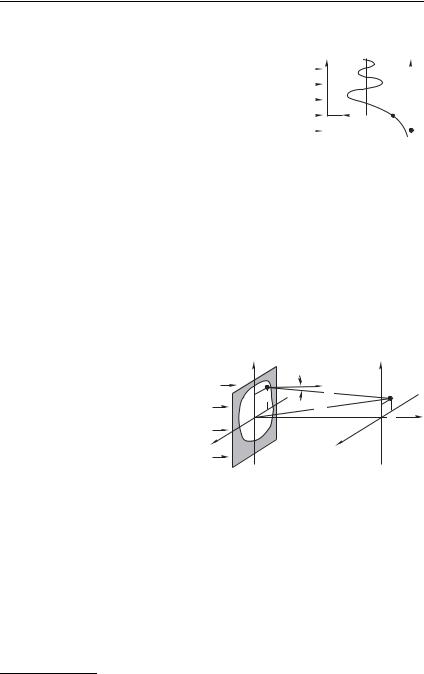

596 |
Дифракция |
[ Гл. 8 |
Вычисляя величину , входящую в фазовый множитель D , мы не можем довольствоваться грубой оценкой 0: ошибка при вычислении фазы колебаний должна быть мала по сравнению с $ и, следовательно, ошибка в вычислении мала по сравнению с длиной волны . Выражение (8.57) запишем в виде
2 2 2 20 2@ 02 @2
идалее, поскольку 2 2 2 0, то
0 1 21 24 |
1 |
2 |
42 |
|
|||
|
|
|
|||||
|
2 |
|
|||||
|
0 |
|
|
|
0 |
|
|
Считая поправку к единице под знаком радикала малой, по- |
|||||||
лучим |
1 4 |
|
12 42 |
|
(8.58) |
||
0 |
0 |
2 0 |
|||||
Разумеется, мы полагаем при этом, что отброшенные члены разложения радикала в степенной ряд малы по сравнению с длиной волны . Обратим внимание, что, согласно граничным условиям Кирхгофа, граничное поле 70 0, @ отлично от нуля лишь на открытой части волнового фронта, поэтому при оценке выражения (8.58) интерес представляют лишь значения 0, @ , лежащие в области отверстия. Очевидно, что последнее слагаемое в (8.58) ограничено величиной 2 2 0 :
12 42 )2 ,
2 0 2 0
где — максимальный линейный размер отверстия. Потребуем теперь, чтобы точка наблюдения находилась столь далеко от отверстия и (или) размер отверстия был столь мал, чтобы выполнялось неравенство 2 2 0 или, что то же,
8 0 |
1 |
(8.59) |
||
|
) |
|||
|
|
|||
Последнее неравенство — условие применимости полученных соотношений — называется условием дифракции Фраунгофера.
Обсуждая ранее условия, при которых справедливы выводы геометрической оптики (в частности, закон прямолинейного распространения света), мы пришли к неравенству (8.32): 2 1, которое, очевидно, противоположно неравенству (8.59). Если геометрическое приближение справедливо при малых расстояниях и (или) больших размерах препятствий , то фраунгоферовы дифракционные картины возникают, напротив, на больших расстояниях и (или) при малых размерах препятствий,
8.9 ] |
Дифракция Фраунгофера |
597 |
расположенных на пути волны. Условие 8 1 эквивалентно следующему: размер отверстия много меньше размера первой
зоны Френеля. Промежуточная область 8 1 называется обычно
областью дифракции Френеля. В этой ситуации размер отвер-
стия и радиус первой зоны Френеля сравнимы между собой.
Итак, при условии (8.59) получим следующее приближенное выражение для :
|
|
0 1 4 |
|
(8.60) |
||
|
|
|
0 |
|
|
|
и вместо (8.56) имеем |
|
|
|
|||
< 0 |
|
0, @ D 0 0 |
|
(8.61) |
||
7 6 |
|
70 |
|
|||
C0 |
||||||
|
|
|
|
|
||
Введем обозначения 0 4, 0 ; тогда формула (8.61) приобретает вид
|
(8.62) |
7 6 70 0, @ D 7 $ |
Последнее соотношение означает, что для нахождения светового поля в точке наблюдения достаточно найти преобразование Фурье граничного поля 70 0, @ : 7 , , %0 4, , взяв в качестве аргументов преобразования 4 0,
0. В частном случае, если граничное поле является функцией одной переменной, 70 0 , то (8.62) приобретает вид
|
|
|
|
|
|
|
|
|
|
|
(8.63) |
|||
|
|
7 6 70 0 D 7 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Сравните (8.63) с полученной ранее формулой (8.43).) |
|
|
|
|
|
|
|
|
||||||
Еще раз отметим, что в (8.62) (или |
|
одномерном |
|
анало- |
||||||||||
ге (8.63)) положение точки наблюдения полностью определяется |
||||||||||||||
параметрами 4, (или параметром 4 — |
|
|
|
|
|
|
|
|
|
|
|
|
||
в случае функции одной переменной). |
|
|
|
|
|
|
|
|
|
|
|
|
||
Обратимся для простоты к одномер- |
|
|
|
|
|
|
|
|
|
|
|
|
||
ной задаче (рис. 8.31). Рассмотрим ко- |
|
|
|
|
|
|
|
÷êå |
|
|
||||
|
|
|
|
|
|
|
|
|
î |
|
|
|
ÿ |
|
лебание в |
точке |
6 как сумму коле- |
|
|
R |
Ê |
ò |
|
|
|
|
|||
|
|
|
|
|
|
|
è |
|||||||
|
d |
|
|
|
|
|
|
|
í |
|
||||
|
|
|
|
|
|
|
äå |
|
|
|||||
|
|
|
|
|
|
|
|
|
þ |
|
|
|
||
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
баний от |
всех вторичных источников |
|
|
|
|
á |
|
|
|
|
|
|
||
|
|
|
à |
|
|
|
|
|
|
|
||||
|
|
|
í |
|
|
|
|
|
R0 |
|
||||
|
|
|
|
|
|
|
|
|
||||||
, заполняющих отверстие. Принимая |
|
|
|
|
|
|
|
|
|
z |
||||
0 |
|
|
|
|
|
|
|
|
|
|
||||
фазу колебания от вторичного источ- |
! sin |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
ника, расположенного в начале коор- |
|
|
|
|
|
|
|
|
|
|
|
|
||
динат, нулевой, найдем фазу колеба- |
|
|
Рис. 8.31 |
|
|
|
|
|
|
|||||
ния от источника |
, находящегося на |
|
|
|
|
|
|
|
|
|||||

598 Дифракция [ Гл. 8
расстоянии 0 от начала координат. При достаточном удалении точки 6 (неравенство (8.59)) разность расстояний 0 можно оценить так: 0 (угол определяет направление на точку наблюдения: 0). Разность фаз колебаний
0 0 0.
Если падающая на щель волна имеет в точке 0 комплексную амплитуду 70 0 , то колебание в точке наблюдения от этого
вторичного источника есть 7 70 0 D |
0 , а суммарное |
колебание |
|
7 6 70 0 D |
0 , |
что совпадает с выражением (8.63), где 4 0 . Еще раз подчеркнем, что при выполнении неравенства (8.59)
поле в точке наблюдения 7 , определяется направлением на эту точку — углом .
Если точка наблюдения смещается вдоль фиксированного направления, приближаясь или удаляясь, так что угол остается неизменным: 0 (и при этом остается справедливым неравенство (8.59)), то значение интеграла (8.63) остается
неизменным: |
|
|
|
|
0 D 4 |
(8.64) |
|
|
7 70 |
В частности, картину дифракции можно характеризовать рас-
пределением интенсивности |
света (потока |
энергии) |
по углам |
|
: : |
|
|
2 |
|
|
70 0 D 4 |
(8.65) |
||
|
: |
|
||
Это распределение : , изображенное в полярных координатах, называют диаграммой направленности.
Продолжая изучение дифракции Фраунгофера, рассмотрим три конкретных примера.
Дифракция Фраунгофера на щели (ширина щели , щель освещается слева плоской нормально падающей волной). Граничное поле 70 0 , возникающие в плоскости 0, примыкающей к непрозрачному экрану со щелью справа, имеет вид изображенный на рис. 8.9 а. Согласно (8.64) для нахождения картины фраунгоферовой дифракции, необходимо найти преобразование Фурье этой функции. Задача полностью аналогична нахождению спектра прямоугольного импульса (см. 1.4). Здесь роль длительности импульса > играет ширина щели , а роль частоты — величина 4 (которую мы назвали ранее
8.9 ] Дифракция Фраунгофера 599
пространственной частотой). Используя эту аналогию, находим
|
|
|
|
) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
$ |
|
|
|
|
||
|
|
|
7 |
2 |
|
|
(8.66) |
||||||||
|
|
|
|
) |
|
$ |
|||||||||
|
|
|
|
2 |
|
|
|
|
|
||||||
Распределение |
интенсивности |
|
: 7 2 |
|
показано на |
||||||||||
рис. |
8.32. |
Ближайшие к |
направлению 0 |
|
направления, |
||||||||||
в которых |
: |
обращается в нуль, определяются условием |
|||||||||||||
2 $, откуда находим |
|
|
|
|
|
I |
|||||||||
|
|
|
(8.67) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
Как |
показывает |
анализ |
формулы |
|
|
|
|
||||||||
(8.66), в интервале углов |
|
|
|
|
|
|
|
|
|
|
sin |
||||
|
|
) |
|
|
|
|
|
|
|
|
/b |
|
/b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Рис. 8.32 |
|||||
сосредоточена подавляющая величина потока энергии (более 80 %). Этот интервал углов (от до ) называют главным максимумом дифракционной картины (легко найти с по-
мощью (8.66), что максимальная интенсивность в ближайшем боковом максимуме, в направлении 3 2 , составляет примерно 0,05 от интенсивности в направлении 0). Мы видим, что сужение щели (уменьшение ) приводит к уширению угла : свет расходится от щели во все более широком интервале углов. Можно сказать и по-другому: с уменьшением ширины щели уширяется пространственный спектр — спектр плоских волн, бегущих от щели.
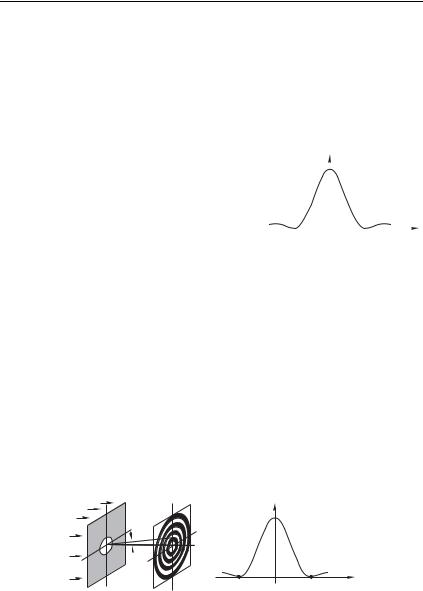
Дифракция Фраунгофера на круглом отверстии
(рис. 8.33). При дифракции плоской волны на круглом отверстии в непрозрачном экране, на удаленной плоскости наблюдения
(т. е. при условии 1, |
— диаметр отверстия) |
|
I |

sin
1,22( /d)
à |
á |
Рис. 8.33
наблюдается картина дифракции, показанная на рис. 8.33 а: центральное яркое дифракционное пятно (которое называется пятном Эйри) окружено чередующимися светлыми и темными кольцами. Соответствующий график : показан на рис. 8.33 б.

600 Дифракция [ Гл. 8
Угловая полуширина пятна Эйри (главного максимума в картине : ) определяется условием
1,22 |
(8.68) |
|
|
В телесном угле сосредоточена подавляющая доля потока энергии ( 80 %) дифрагированной волны.
Дифракция Фраунгофера на решетке. Рядом со щелью, дифракцию на которой мы рассмотрели выше (эта картина дифракции описывается функцией 7 , см. формулу (8.66)), расположим параллельно еще одну такую же щель, центр которой находится в точке 0 , рис. 8.34. Расстояние от второй щели до точки наблюдения (от любого элемента этой щели) на ве-
личину |
меньше расстояния между соответствующим |
||||||||||
|
|
|
|
|
|
|
|
|
|
элементом первой щели и точкой наблю- |
|
|
|
|
|
|
|
|
дения (рис. 8.34). Соответственно, фаза |
||||
|
|
|
|
||||||||
|
|
|
|
|
|
Ê |
точке |
|
колебаний отличается на величину |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
# , |
(8.69) |
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
наблюдения |
|
||||
|
d |
|
|
|
|
поэтому колебательный процесс, создан- |
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
ный второй щелью в точке наблюдения, |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
O |
|
|
|
z описывается функцией 7 D'. Волны, |
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
Рис. 8.34 |
|
|
посылаемые в точку наблюдения двумя |
||
|
|
|
|
|
|
|
|
щелями, интерферируют, суммарный ко- |
|||
лебательный процесс в точке наблюдения есть 7 7 D'. Если расположить рядом еще одну щель, сдвинутую относительно первой на расстояние 2 (и на расстояние от второй), то получим суммарное колебание 7 7 D' 7 D 2'. Наконец, если мы имеем решетку, состоящую из ! параллельно рас-
положенных щелей (период решетки |
), то суммарное колебание |
|
имеет вид |
|
|
1 |
(8.70) |
|
7 |
D' |
|
|
0 |
|
Сумму, входящую в (8.70), мы уже находили ранее (1.16) (сумма колебаний, фазы которых составляют арифметическую прогрессию) с помощью векторной диаграммы, показанной на
рис. 1.7. В нашем случае # |
и мы получаем |
|
|||||||
7 |
B $ 2 |
|
|
(8.71) |
|||||
|
|
|
|||||||
|
|
|
|
$ 2 |
|
|
|||
Распределение интенсивности : по углам описывается |
|||||||||
формулой |
|
|
|
|
|
|
2 |
|
|
|
2 B $ 2 |
|
|||||||
: 7 |
|
(8.72) |
|||||||
|
|
|
$ 2 |
|
|||||
