студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

9.1 ] Фазовая и групповая скорость. Формула Рэлея 641

Мы получаем

7 , D #0 0

Запишем окончательно, учитывая соотношение (9.1):

7 , D #0 0

Полученный нами результат означает следующее: волновой пакет, форма которого задается «огибающей» , распространяется в среде без искажения и на расстоянии от излучателя воспроизводит закон модуляции с запаздыванием по време-

ни , равным

Из последнего равенства находим скорость волнового пакета

4

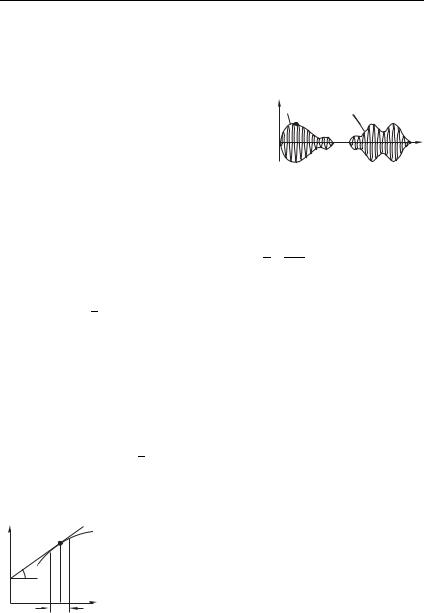
Иллюстрацией является рис. 9.4, на котором показано положение волнового пакета вблизи излучателя (к моменту времени,

ляющего фазовую скорость монохроматической волны частоты0: # 0 0 , т. е. групповая скорость — скорость, с которой переносится сигнал, отличается, вообще говоря, от фазовой скорости «несущей волны» D #0 0 . Поскольку волновой пакет не искажается (не «деформируется») в процессе движения, для определения групповой скорости можно следить за движением любой точки волнового пакета, например, за движением максимума огибающей (точкой на рис. 9.4), т. е. максимума амплитуды, либо точкой — локального максимума амплитуды, либо любой другой точкой волнового пакета.

Согласно современным представлениям универсальная физическая константа , равная скорости света в вакууме, определяет

предельную скорость распространения любых сигналов. В частности, групповая скорость любого пакета, какова бы ни была

его форма, в какой бы среде он ни распространялся, какова

21 Основы физики. Т. I

бы ни была физическая природа волны, не может превосходить скорость света в вакууме. Что касается фазовой скорости, то

она может быть любой, как больше, так и меньше скорости света в вакууме, поскольку скорость перемещения волновой поверхности идеальной, бесконечно длящейся синусоидальной волны не связана с переносом какой-либо энергии или передачей информации.

Найдем связь между фазовой и групповой скоростью. Пусть закон дисперсии задан в виде зависимости фазовой скорости от длины волны . Используя выражение для фазовой скорости , запишем . Тогда находим 4

Формула (9.6), связывающая фазовую и групповую скорость, называется формулой Рэлея.

Если & 0 (фазовая скорость растет с ростом длины вол-

ны), то 4 ' — групповая скорость меньше фазовой: огибающая4 отстает при движении волнового пакета от несущей

гармонической волны D #0 0 (например, максимум амплитуды движется медленнее, чем волновые поверхности). Такого рода

дисперсия называется нормальной. В обратном случае ' 0 имеет место аномальная дисперсия.

Если фазовая скорость всех волн, составляющих волновой

пакет, одинакова ( , независящая от ), то 0 и

дисперсия отсутствует — групповая скорость равна фазовой. Часто свойства оптически прозрачной среды задаются зави-

симостью показателя преломления среды от частоты . Напомним, что согласно определению и следовательно

при & 0 4 ' — имеет место нормальный закон дисперсии,

а при ' 0, 4 & — аномальная дисперсия.

Выше мы рассмотрели ситуацию, когда можно использовать линейный закон дисперсии (9.5). Именно в этом случае волновой

, дисперсия не приводит к деформации волнового пакета при распространении в среде. Из рис. 9.6 ясно, что точка пересечения касательной с осью ординат как раз и определяет величину

групповой скорости 4 # .

9.2. Дисперсия электромагнитных волн

Классическая теория, созданная Лоренцем, основана на идеализированной модели среды, в которой распространяется электромагнитная волна. Согласно этой модели среда представляет собой набор невзаимодействующих между собой атомов (наилучшим приближением является газообразная среда). В простейшем случае предполагается, что в атоме имеется один «оптический» электрон, квазиупруго связанный с ядром: сила, действующая на этот электрон со стороны поля ядра (экранированного частично электронами внутренних оболочек) линейно связана со смещением из положения равновесия: упр . Таким образом, электрон в атоме рассматривается как линейный осциллятор (см. § 2.1). Вынужденные колебания осциллятора обусловлены полем электромагнитной волны: внешняя сила, действующая на электрон, есть D- , где D — заряд электрона, 0D# — электрическое поле монохроматической волны частоты , бегущей в среде.

Колеблющийся электрон сам становится источником электромагнитной волны, благодаря чему его свободные колебания затухают; это обстоятельство учитывается феноменологически введением «силы трения», пропорциональной скорости и равной

*(так называемое радиационное затухание, см. § 6.5). Уравнение движения электрона имеет вид

Вэтом решении опущены две константы интегрирования v0

иr0. Тем самым подразумевается, что в среде нет ни макроскопического заряда, ни макроскопических токов, которые были бы обусловлены положениями и скоростями элементарных зарядов в среде.

Смещение из положения равновесия приводит к появлению дипольного момента атома D , который, как ясно из (9.8), изменяется по гармоническому закону, пропорционально меняющемуся по гармоническому закону электрическому полю волны. Важно обратить внимание на то, что коэффициент про-

порциональности, связывающий и (и называемый атомной поляризуемостью)

является, в общем случае, комплексным, а это означает, что колебания происходят со сдвигом фазы по отношению к колебаниям , причем фазовый сдвиг зависит от частоты. Колеблющиеся диполи вещества сами становятся источниками излучения. Это переизлучение происходит с той же частотой . Переизлученные колеблющимися диполями волны, складываясь (интерферируя) с первичной волной, образуют волну, распространяющуюся в среде, причем отставание по фазе вторичных волн по отношению к первичной волне (зависящее от частоты), приводит к тому, что фазовая скорость результирующей волны также становится зависящей от частоты — в этом суть явления дисперсии.

Рассматриваемая нами среда достаточно разрежена, она состоит, как было отмечено, из невзаимодействующих, т. е. достаточно далеко отстоящих друг от друга, атомов. Тем не менее, в пределах элемента объема, малого по сравнению с длиной волны, в котором поле можно считать однородным (одинаковым в каждый момент времени во всех его точках), находится достаточно большое число атомов. Например, для видимого света5 10 7 м, и в объеме, равном 3, содержится около 4 105 атомов газообразного вещества при нормальных условиях. Итак, мы можем считать, что большое число осцилляторов в пределах малого элемента объема в каждый момент времени имеют один и тот же дипольный момент. Тогда поляризация среды (дипольный момент единицы объема среды) равен !p, где ! — число осцилляторов в единице объема.

Используя (9.9), находим

Итак, поляризация среды P колеблется с частотой , равной

частоте волны, бегущей в среде. Согласно определению диэлектрическая восприимчивость среды H — это коэффициент про-

порциональности, связывающий P и E: <0H . Мы получаем

646 Дисперсия волн [ Гл. 9

Соответствующее выражение для диэлектрической проницаемости < 1 H есть:

.

Обратим внимание на еще одно важное обстоятельство: поскольку диэлектрическая проницаемость < является в общем случае комплексной величиной < < < , то и показатель преломления , и следовательно, волновое число — также комплексные величины:

7 , D # комплексную величину , находим 7 , D D # . Мы видим, что волна 7 ,

не является плоской волной в обычном понимании, поскольку по

мере роста амплитуда волны D экспоненциально убывает (показатель экспоненты — действительное отрицательное число), волна затухает, причем затухание связано с мнимой частью волнового числа (и, следовательно, с мнимой частью показателя преломления ). Действительная часть и определяют фазовую скорость волны .

Итак, рассмотрим различные ситуации, основываясь на об-

Нормальная дисперсия. Сравним величины 02 2 и 25, входящие в знаменатель второго слагаемого в (9.14). Пусть

0 , тогда 2 2 0 . Величина 5, как

0

известно, определяет ширину резонансной кривой при вынужденных колебаниях гармонического осциллятора. Пусть частота волны далека от резонансной частоты осциллятора 0, тогда5 и следовательно 0 25, т. е. мнимое слагаемое в знаменателе (9.9) и (9.14) мало по сравнению с действительным и им можно пренебречь. Тогда

9.2 ] Дисперсия электромагнитных волн 647

т. е. диэлектрическая проницаемость — действительное число. Действительным является также и волновое число: 0, а это означает отсутствие затухания — среда оказывается прозрачной для электромагнитной волны. Физически этот результат понятен: при частотах внешней силы, далеких от резонансной частоты осцилляторов, амплитуда вынужденных колебаний мала; волна, распространяясь в среде, практически не отдает энергию осцилляторам, т. е. не поглощается.

Собственные частоты «оптических» электронов многих веществ лежат в далекой ультрафиолетовой области спектра, поэтому для волн видимой области 0 и условие 5 выполняется.

Кроме того, если концентрация осцилляторов достаточно ма-

Зависимость (9.16) показана на рис. 9.7 (штриховой линией обозначена область графика , в котором перестает выполняться неравенство 5 и, следовательно, указанная зависимость уже не справедлива).

Эмпирическая формула

где и — константы, была известна задолго до создания электронной теории дисперсии. Она может быть получена из (9.16), причем константы и связаны с характеристиками среды равенствами

сто нормальная дисперсия: растет с ростом частоты. Левая ветвь соответствует частотам, меньшим 0 (в частности, видимый свет). Для этих частот показатель преломления больше единицы и, следовательно, фазовая скорость меньше скорости света в вакууме ' . Для частот & 0 (например, рентгеновский диапазон спектра) ' 1 и & , что, как мы

отмечали ранее, не противоречит специальной теории относительности, согласно которой скорость любых тел или сигналов ограничена величиной , что не имеет отношения к фазовой скорости монохроматической волны.

Eсли выполнено сильное неравенство 0 (и тем более50), то формула (9.15) дает:

Эта формула справедлива приближенно как для волн рентгеновского диапазона, так и для радиоволн в ионосфере, которая представляет собой плазму, т. е. полностью ионизованный газ, дисперсия волн в которой обусловлена свободными электронами. В последнем случае формула (9.19) справедлива, поскольку на свободные электроны не действует квазиупругая сила, связывающая электроны в атоме, поэтому 0 0 и сильное неравенство0 выполняется даже для низкочастотных радиоволн.

Соотношение (9.19) позволяет объяснить особенности характера распространения радиоволн в ионосфере.

При ' 0 (что соответствует длинам волн 10 м) пока-

становится чисто мнимым, амплитуда волны экспоненциально спадает и волна не проникает вглубь ионосферного слоя; при этом коэффициент отражения (определяемый, согласно формулам Френеля, действительной частью ), равен единице. Напомним, что, в частности, при нормальном падении

1 1 2 1, поскольку 0.

Таким образом, полное внутреннее отражение происходит при любом угле падения.

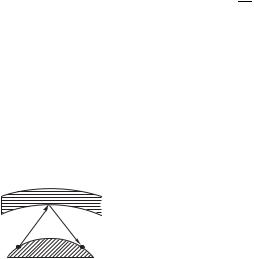
Отражение длинных радиоволн от ионосферного слоя используется для дальней радиосвязи (рис. 9.8), когда передатчик

1 2 2 , легко получить простую связь между фазовой и

0

групповой скоростью. Возводя обе части последнего равенства в

9.2 ] Дисперсия электромагнитных волн 649

Последнюю связь удобно использовать вместо формулы Рэлея,

если речь идет о законе дисперсии (9.20).

Закономерности поведения электромагнитных волн в ионосфере во многом подобны их поведению в металлах. И в том,

и в другом случае дисперсия обусловлена взаимодействием волны со свободными электронами, на которые не действует

которая получается из общего соотношения (9.14) при 0 0. При низких частотах, таких, что 5 и, следовательно, 225 получаем из (9.22)

то из (9.23) следует, что показатель преломления является комплексным числом с равными действительной и мнимой частью

2 ,

Из неравенства 1 следует, что амплитуда волны быстро уменьшается по мере проникновения в металл (глубина проникновения 1 много меньше длины волны), при этом коэффициент отражения, определяемый действительной частью показателя преломления, близок к единице:1 1 2 1 при 1 (при нормальном падении) — волна практически полностью отражается.

В случае высоких частот 5 приходим к формуле (9.20), из которой можно сделать те же выводы, которые относились

650 Дисперсия волн [ Гл. 9

ранее к дисперсии радиоволн в ионосфере. В частности, при& 0 показатель преломления становится действительным, а металл прозрачен для волны (обычно условие & п начинает выполняться для металлов в рентгеновской области частот). В оптическом диапазоне частот ситуация не столь проста, о чем говорит хотя бы эффект избирательного отражения — желтый цвет золота и меди. Это значит, что помимо электродинамики, здесь важна атомная физика.

Аномальная дисперсия. Выше мы рассматривали дисперсию в области частот, далеких от собственной частоты осцилляторов:0 5. В этом случае диэлектрическая проницаемость < является действительной функцией, среда оказывается прозрачной для волны (отсутствует поглощение) и показатель преломления растет с ростом частоты, т. е. имеет место нормальная дисперсия.

Обратимся теперь к случаю, когда частота волны близка к собственной частоте атомных осцилляторов. Одну важную особенность мы уже отмечали: если 0 5, то функция < оказывается комплексной. Поглощение волны средой в этом случае обусловлено передачей энергии волны колеблющимся осцилляторам, амплитуда вынужденных колебаний которых становится особенно большой, когда частота силы, раскачивающей колебания (т. е. частота колебания электрического поля волны), близка к резонансной.

Детальное исследование общего соотношения (9.14) показывает, что в области, где волна испытывает сильное поглощение, характер дисперсии является аномальным: в области частот0 5 показатель преломления

атомных осцилляторов: чем больше амплитуда вынужденных колебаний, тем сильнее поглощение волны в среде; и именно в пределах ширины полосы резонансной кривой имеет место аномальный характер дисперсии. В области частот, далеких от резонансной, кривая на рис. 9.9 совпадает с кривой, показанной на рис. 9.7.