студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

3.4 ] Автогенератор Ван-дер-Поля 471

наклона прямой на линейном участке). Правильная зависимость : ,с должна описывать, что происходит, когда ,с становится достаточно большой отрицательной величиной (,с ' ,1) (и при этом : 0) и что происходит при достаточно больших положительных ,с (,с & ,2) и при этом : :- (насыщение).

Итак, с учетом нелинейности характеристики лампы при больших амплитудах колебаний, правая часть уравнения (3.20) —

шается, как только величина ,c выходит из области ,1 ' ,c ',2; при этом 9 ,c 0 и Æ 2+ становится существенно положительной величиной.

Итак, рассмотрим ситуацию, когда амплитуда колебаний стала достаточно большой, так что значение ,c при колебаниях выходят за рамки рассмотренной области (рис. 3.8). Начнем с момента времени 1, когда ,c 0 и начинает расти. Пропорционально, в соответствии с законом (3.21), изображенном на рис. 3.8 растет анодный ток вплоть до момента времени 2, когда наступает насыщение : :-. Далее (см. рис. 3.8 б) значение ,c продолжает при колебаниях нарастать, а затем уменьшается,

оставаясь, вплоть до момента време-

линейного коридора, поэтому и анодный ток : пропорционально

472 Параметрические колебания. Ангармонический осциллятор [ Гл. 3

падает (падающий участок : на рисунке, и к моменту времени 4, когда напряжение на конденсаторе , становится равным запирающему напряжению ,1, анодный ток становится равным нулю.

Аналогичным образом с помощью рисунков 3.8 и 3.10 можно проследить процесс и далее.

Итак, мы видим, к чему приводит нелинейность характеристики лампы: при большом размахе колебаний напряжения на конденсаторе , (которые происходят, как показано на рисунке, по гармоническому закону) изменение анодного тока со временем имеет существенно другую форму: анодный ток представляет собой последовательность почти прямоугольных импульсов с крутыми участками роста и спада (на отрезках времени 1 2 и 3 4) и горизонтальным участком постоянных значений : (отрезок времени 2 3, : :- — ток насыщения и отрезок4 5 — нулевое значение : ).

График зависимости +12 +% : от (где +12, + и % —

графика , , в моменты, когда напряжение на конденсаторе

равно нулю и, следовательно, ток : %, максимален, т. е. равен амплитудному значению :. После толчка, создающего скачок тока :, получим :1 : :. За короткое время толчка > 2 1 4 3 и т. д. суммарный поток, пронизывающий катушку +, сохраняется

+ : +12 : 0,

3.4 ] Автогенератор Ван-дер-Поля 473

откуда : : +12 +. За время действия толчка анодный ток, как видно из графика : на рис. 3.10 изменяется от 0 до максимальной величины :-, т. е. : :- и мы получаем

Далее, до очередного толчка, контур свободен от внешнего воздействия и, в силу экспоненциального затухания, амплитуда уменьшается, ее значение перед очередным толчком равно

Æ1 2

:2 :1D

( 2 — время между толчками).

Условие стационарности: значение амплитуды перед каждым очередным толчком (а значит и после каждого очередного толчка) не меняется, т. е. :2 :1 :

: : 12+ D Æ1 2,

откуда находим стационарное, установившееся значение амплитуды автоколебаний

: 12+ Æ1 2

1 < Æ2 D

Если контур обладает малым затуханием (добротность велика), то скачки тока : оказываются малыми по сравнению с установившимся значением :. Используя D Æ1 2 1 Æ 2,

находим : 2+12:- +Æ .

Заметим в заключение, что все основные свойства автоколебательной системы, рассмотренные нами на примере лампового генератора, сохраняются, если использовать вместо лампы полупроводниковый триод.

Г л а в а 4

КИНЕМАТИКА ВОЛН

Понятие волны — одно из важнейших в физике. Современная физика изучает и волны на море, и сейсмические волны в Земле, и волны звука в твердых телах, жидкостях и газах, и электромагнитные волны (в том числе свет) и, наконец, волны вероятности, которые используются в квантовой физике для описания поведения электронов, атомов и других микрообъектов. Важно подчеркнуть, что наука о волнах использует единый математический аппарат для описания волн любой физической природы — в этом и проявляется общность волновых закономерностей.

4.1. Основные понятия и определения. Простейшие типы волн. Волновое уравнение

Что такое волна? Очень трудно дать исчерпывающее определение этого понятия, не обращаясь к математическим формулам, ибо любое определение не может охватить всего многообразия процессов, которые принято называть волнами. Для первоначального знакомства с волнами достаточно понимать их как процесс распространения в пространстве колебаний, возникающих

врезультате некоторого возмущения. Таким возмущением может быть и изменение давления в каком-либо месте упругой среды, и изменение электрического или магнитного поля в некоторой точке пространства, и изменение уровня поверхности жидкости

вкаком-либо месте (например, от брошенного на гладкую поверхность воды камня). Во всех этих случаях возмущение начинает с конечной скоростью распространяться в пространстве.

Волновой процесс развивается и во времени, и в пространстве, поэтому в отличие от колебательного процесса, который описывается функцией времени 9 , волновой процесс должен описываться функцией координат и времени 9 , , , (или, коротко, 9 , ). На первом этапе мы не будем интересоваться

странении в ней звуковой волны, либо 9 — это напряженность электрического или магнитного поля при распространении электромагнитной волны, либо это волна какой-либо иной природы.

4.1 ] Простейшие типы волн. Волновое уравнение 475

Начнем математическое описание с наиболее простой ситуации — плоских волновых возмущений: будем считать, что волновое возмущение 9 зависит только от одной координаты (скажем от координаты ). Пусть в какой-то момент времени мы определили распределение возмущения в пространстве, т. е. определили 9 как функцию координаты (рис. 4.1 а). (Мы договорились, что 9 зависит только от , т. е. если рассмотреть любую плоскость, перпендикулярную оси (плоскость ), то в любой точке этой плоскости величина 9 одна и та же, независимо от координат , этой точки). Можно сказать, что

на расстояние , где — cкорость распространения возмущения. Предположим, что пространственная форма возмущения не изменилась, т. е. вторая фотография изображает тот же «волновой пакет», только сдвинутый в пространстве на расстояние :

Равенство (4.1) означает, что изменения во времени возмущения 9 (колебание величины 9) в плоскости происходят точно так же, как и в плоскости , лишь запаздывая по времени на . Какова должна быть зависимость 9 от координаты и времени , чтобы равенство (4.1) было справедливо? Легко догадаться, что она должна иметь вид

т. е. функция 9 должна зависеть от комбинации аргументов и вида: . Действительно в этом случае равенство (4.1) выполняется, поскольку если заменить на , а на , то величина не изменится:

всилу того, что .

Итак, зависимость вида (4.2) соответствует нашему интуитивному представлению о волне, как о возмущении, которое распространяется в пространстве с конечной скоростью. В нашем случае & 0, т. е. волна бежит вправо, в положительном направлении оси . Аналогичным образом можно показать, что функция 9 описывает волну, бегущую справа налево.

Обозначая аргумент функции 9 через 0 (0 ), найдем связь между производными 9 по координате и времени:

Сравнивая вторые производные функции 9 по и по (4.3), замечаем, что они отличаются множителем 2, и мы получаем

Соотношение (4.4) называется волновым уравнением. В более общем случае, когда возмущение 9 зависит не только от-координаты, но также от - и -координат, волновое уравнение выглядит следующим образом:

2( 2( 2( 1 2(

2 2 2 2 2

Левая часть последнего уравнения коротко записывается с помощью оператора Лапласа 2 .2.2 .2.2 .2.2, волновое уравнение приобретает компактный вид:

Вообще говоря, уравнение (4.5) описывает волновые процессы более общего характера, чем только волны вида 9 . Мы можем дать теперь несколько формальное, но более общее определение понятия волны. Любая физическая величина

9 , , подчиняющаяся уравнению (4.5), может быть названа

волной.

Рассмотрим несколько важных примеров простейших типов волн.

Плоская монохроматическая волна. Пусть возмущение описывается функцией координат и времени вида

где , и — константы. Смысл константы ясен: при фиксированном (т. е. в любой плоскости, перпендикулярной оси )

$ ( 0, 1, 2, ), амплитуда колебаний максимальна и равна 2 (напомним, что — амплитуды встречных бегущих

волн).

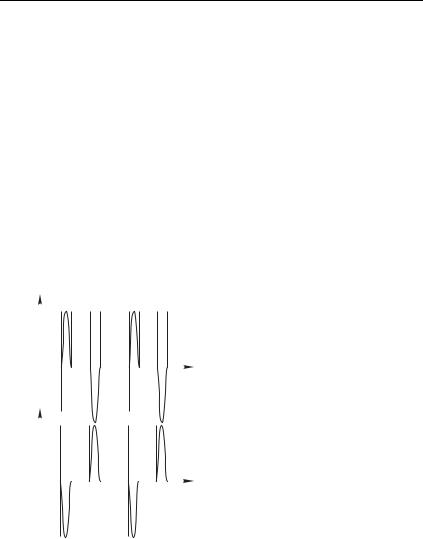
Точки максимальной амплитуды называются пучностями, которые располагаются точно посередине между узлами, т. е. на расстоянии 4 от ближайших узлов (и 2 друг от друга).

Заметим, что при тех значениях , где величина отрицательна, функцию 9 , можно записать в виде

9 , $ ,

откуда ясно, что отрицательность амплитуды означает лишь, что колебания происходят в противофазе (со сдвигом фазы на $) по сравнению с колебаниями при тех , где & 0

встречными волнами одинаковой частоты и амплитуды, нет

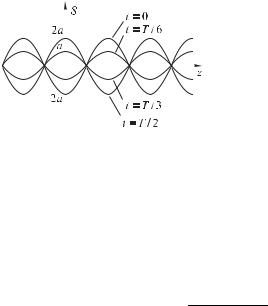
перемещающихся волновых поверхностей (так как нет аргумента вида ), поэтому волна (4.14) называется стоячей волной.

Сферическая волна. Волна, описываемая уравнением

называется сферической. В уравнении (4.16) — расстояние от начала координат (где расположен источник волны) до точки наблюдения , ,

2 2 2 ,

— волновое число. Обратная пропорциональность амплитуды радиусу — свойство сферически симметричного решения уравнения (4.5). Понятен смысл названия «сферическая волна»: согласно (4.16) колебания 9 происходят синфазно во всех точках пространства, отстоящих от источника на заданном расстоянии , т. е. волновые поверхности — это сферы, центр которых (источник волны) находится в начале координат. Обратим внимание на различие уравнений (4.12) и (4.16). В уравнении плоской волны аргумент косинуса содержит ска-