
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
2.6 ] |
Вынужденные колебания гармонического осциллятора |
441 |
|
Решение же уравнения (2.62) легко угадать. Будем ис- |
|
кать это решение в виде |
|
|
|
G D#, |
(2.64) |
т. е. мы полагаем, что гармоническое внешнее воздействие возбуждает в осцилляторе гармоническое колебание, частота которого совпадает с частотой внешнего воздействия, а комплексный множитель G D5 # определяет амплитудуи начальную фазу B вынужденных колебаний. Это предположение необходимо проверить. Подставив предполагаемое решение (2.64) в уравнение (2.62), убедимся, что можно подобрать комплексный множитель G так, чтобы уравнение (2.62) обратилось в тождество.
Действительно, уравнение (2.62) является линейным, т. е. содержит неизвестную функцию и ее производные только в первой степени. В частности, над функцией в левой части (2.62) выполняется лишь линейная операция дифференцирования, которая оставляет неизменным вид экспоненциального множите-
ля D# |
|
|
|
|
2 |
|
|
2D# |
|
|
D# D#, |
# |
|
(2.65) |
|||||
|
|
|
|||||||
|
|
2 |
D |
|
|
||||
|
|
|
|
|
|||||
Подставляя (2.64) в (2.62) и учитывая тождества (2.65), на- |
|||||||||
ходим |
|
|
|
|
|
|
|
|
|
|
2GD# |
|
|
2 |
# |
2 |
# |
||
|
|
|
2Æ G D# 0GD |
0D |
|
||||
|
|
|
|
||||||
Множитель D# содержится как в правой части последнего уравнения, так и в его левой части. После сокращения на этот множитель мы приходим к алгебраическому уравнению для определения G, откуда получаем
|
|
2 |
|
|
|
G |
|
0 |
|
|
(2.66) |
|
2 C |
|
|||
2 |
2Æ |
|
|
||
0 |
|
|
|
||
Запись G подчеркивает, что найденное нами комплексное число G зависит от частоты вынуждающей силы. Таким образом, мы показали, что функция , определяемая формулой (2.64), действительно является решением уравнения (2.62), если G определяется соотношением (2.66).
Предоставляем читателю самостоятельно показать, что модуль комплексного числа G есть
|
|
|
2 |
|
|
|
|
G |
|
0 |
|
|
, |
(2.67) |
|
|
|
|
|
|
|||
|
2 |
2 2 |
4Æ2 2 |
||||
|
0 |
|
|
|
|
|
|

442 Колебания в линейных системах [ Гл. 2
а его аргумент B определяется формулой
B # |
2Æ |
|
(2.68) |
||
2 2 |
|||||
|
|
|
0 |
|
|
Итак, мы нашли комплексное решение уравнения (2.62), |
|||||
имеющее вид |
|
|
|
|
|
D # 5 # , |
(2.69) |
||||
где и B определяются выражениями (2.67) и (2.68). |
|||||
Соответствующий реальный |
колебательный |
процесс 9 |
|||
имеет вид |
|
|
|
|
1 |
|
|
|
|
(2.70) |
|
91 B |
|||||
Подчеркнем еще раз, что речь идет о гармоническом осцилляторе, т. е. о линейной колебательной системе (в которой сила, возвращающая осциллятор в положение равновесия, прямо пропорциональна смещению). Мы получили исключительной
важности результат.
Гармоническая внешняя сила частоты возбуждает в осцилляторе вынужденные колебания, которые происходят также по гармоническому закону и имеют ту же частоту .
Функция определяет амплитуду вынужденных коле-
баний — ее зависимость от частоты внешней силы; ее называют амплитудной характеристикой осциллятора (точнее
есть отношение амплитуды вынужденных колебаний к амплитуде внешнего воздействия, что ясно из (2.70)), а функция B (2.68) дает сдвиг по фазе между вынужденными коле-
баниями и колебаниями внешней силы и называется фазовой характеристикой.
Комплексную функцию G 5 # называют частотной (или амплитудно-фазовой) характеристикой (иногда используют термин передаточная функция).
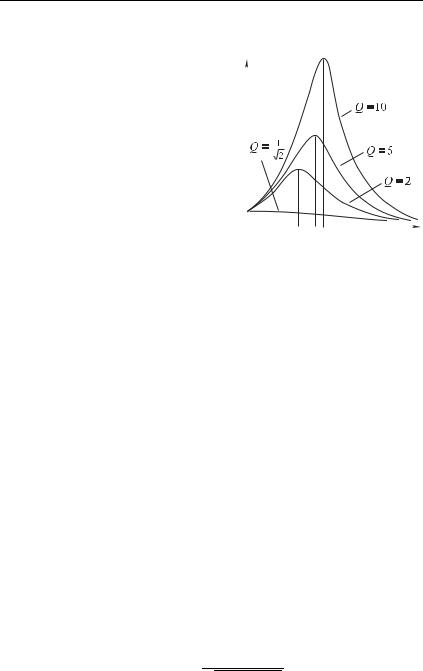
Исследуем подробнее полученные нами зависимости амплитуды вынужденных колебаний и сдвига фазы от частоты внешней силы.
Зависимость интенсивности колебаний (квадрата амплитуды) от частоты внешней силы имеет вид
2 |
|
|
4 |
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
(2.71) |
|||
|
2 |
2 2 |
4Æ |
2 2 |
|
||||||||
|
|
|
0 |
|
|
|
|
|
|
||||
Разделив числитель и знаменатель на 4Æ2 02 и используя |
|||||||||||||
соотношение C 0 2Æ (см. ниже, задача 4), получаем |
|
||||||||||||
2 |
|
|
|
|
92 |
|
|
|
|
|
|
(2.72) |
|
|
2 |
1 |
2 2 |
2 |
|
|
2 2 |
||||||
9 |
|
|
|
||||||||||
|
|
0 |
|
|
0 |
|
|
||||||

444 |
Колебания в линейных системах |
[ Гл. 2 |
(эта величина больше, чем на частоте 0, когда амплитуда вынужденных колебаний равна C).
Таким образом, максимум амплитуды приходится на частоту, несколько меньшую 0, однако при C 1 мы имеем из (2.73) и (2.74) уже отмеченный результат: максимальная амплитуда, равная 0C, наступает при 0.
Наконец, рассмотрим вопрос об остроте резонансной кривой колебательной системы с большой добротностью. При каком отклонении частоты от значения 0 амплитуда вынужденных
колебаний заметно уменьшается (скажем в 2 раз)? Как видно из (2.72), это происходит при
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
C2 1 |
|
|
|
|
|
|
|
2, |
|
|
|
|
|||||||
0 |
0 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
откуда находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
1 |
1 |
|
|
1 |
1 |
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
292 9 |
|
492 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
С точностью до членов порядка 1C2 имеем |
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
1 |
|
|
или |
|
0 1 |
|
1 |
|
, |
|||||||||
0 |
29 |
|
|
|
|
29 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и мы получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
0 |
|
Æ |
|
|
|
(2.75) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|
|
|
Итак мы нашли полуширину резонансной кривой на уровне
1 2 , которая равна величине затухания Æ.
Заметим наконец, что при амплитуда вынужденных колебаний стремится к нулю: знаменатель в (2.72) при0 2 1 имеет вид
|
|
2 2 |
|
2 |
|
|
|
4 |
||
C2 1 |
|
|
|
|
|
|
C2 |
|
|
, |
0 |
0 |
0 |
||||||||
если C 1. Поэтому получаем
2
0 |
(2.76) |
||
|
|
|
|
|
|
||
при 0 Выражение для фазовой характеристики (2.68) можно пере-
писать в виде
B # |
|
0 |
|
|
(2.77) |
|
9 1 |
0 |
2 |
||
|
|
||||
|
|
|
|
||
2.7 ] |
Гармонические колебания в линейных стационарных системах |
445 |
|||||||||
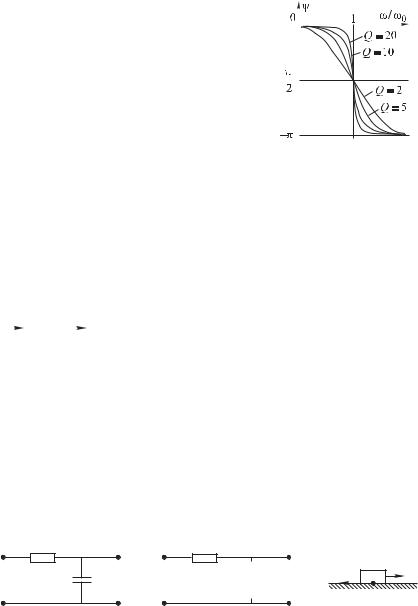
Эта зависимость |
для разных |
значений |
C показана |
на |
|||||||
рис. 2.16. |
|
|
|
|
|
|
|
|
|
|
|
Следует обратить |
внимание, |
что |
|
|
|
||||||
|
|
|
|||||||||
с ростом добротности фаза B меняет- |
|
|
|
|
|||||||
|
|
|
|
||||||||
ся все круче вблизи резонансной часто- |
|
|
|
||||||||
ты, изменяясь от значения B 0 |
при |
|
|
|
|||||||
' 0 до значения B $ при & 0, |
|
|
|
||||||||
т. е. если колебательная система име- |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
ет высокую добротность, то при ча- |
|
|
|
||||||||
стотах ' 0 вынужденные колеба- |
|
|
|
||||||||
ния |
происходят практически синфазно |
|
|
|
|||||||
с колебаниями внешней силы, а |
при |
|
|
|
|||||||
|
|
|
|||||||||
& 0 — в противофазе с колебаниями |
Рис. 2.16 |
|
|
||||||||
внешней силы. |
|
|
|
|
|
|
|
|
|
|
|
2.7. Гармонические колебания в линейных стационарных системах
При изучении общих свойств линейных систем (фильтров) обычно не интересуются их конкретным устройством. Систему изображают в виде блок-схемы (рис. 2.17). Внешнее воздействие
|
|
|
|
|
7 называют «входным сигналом» фильтра, а |
|
f (t) |
|
|
S(t) |
искомую зависимость 9 — выходным сигна- |
||
L |
|
|||||
|
|
|
|
лом (или откликом) фильтра. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.17 |
|
Квадратик + представляет |
собой некото- |
|||
|
рое устройство, преобразующее |
входной сиг- |
||||
|
|
|
|
|
||
нал 7 в выходной сигнал 9 . Тот факт, что 9 является откликом на внешнее воздействие 7 , будем записывать в виде равенства 9 + 7 , которое означает, что в результате действия входного сигнала 7 на линейную систему + получаем сигнал на выходе 9 .
Гармонический осциллятор является одним из примеров линейной колебательной системы, т. е. системы, колебания в ко-
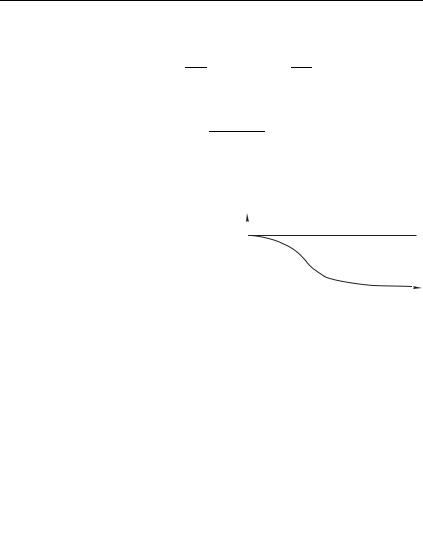
торой подчиняются линейному уравнению (напомним, уравнение линейно, если искомая функция 9 и ее производные входят в уравнение только в первой степени). Другие примеры линейных систем показаны на рис. 2.18.
|
R |
|
|
R |
|
f (t) |
f (t) |
S(t) |
|
|
S(t) |
||
C |
f (t) |
|
L |
|||
|
|
|
|
|
|
Fòð x
à |
á |
â |
Рис. 2.18

446 |
Колебания в линейных системах |
[ Гл. 2 |
На рис. 2.18 а изображена %-цепочка, колебания в которой возбуждаются внешней ЭДС 7 . Искомой функцией является изменение напряжения на конденсаторе 9 .
На рис. 2.18 б показана +-цепочка. Ищется закон изменения напряжения на катушке индуктивности.
На рис. 2.18 в — простой механический пример: изучается движение тела массы под действием внешней силы, меняющейся во времени по закону 7 , тело движется в среде с вязким трением (сила трения пропорциональна скорости тр * ). Ищется закон изменения скорости 2 .
Покажем, что во всех этих случаях поведение систем также описывается линейным уравнением с постоянными коэффициентами, и гармоническое внешнее воздействие приводит к возникновению в этих системах вынужденных гармонических колебаний , происходящих с той же частотой, т. е. G D#. Найдем также частотные характеристики G этих систем.
1. Рассмотрим %-фильтр (см. рис. 2.18 а). Закон Кирхгофа
имеет вид
/ ;5 7
(сумма падений напряжения на сопротивлении / и на конденсаторе / % равна внешней ЭДС 7 . Искомой величиной (выходным сигналом фильтра) является напряжение на конденсаторе 9 / %. Тогда напряжение на сопротивлении / % 9 и мы получаем
|
1 |
|
1 |
|
9 |
|
9 |
|
7 |
; |
; |
Вновь приходим к линейному уравнению с постоянными коэффициентами.
Каков процесс вынужденных колебаний, если внешним воздействием является гармоническое колебание единичной амплитуды? Уравнение, описывающее процесс колебаний имеет вид
|
1 |
|
1 |
|
9 |
|
|
|
|
; |
; |
Так же, как и в случае гармонического осциллятора, перейдем к комплексной форме записи:
|
1 |
|
1 |
D# |
(2.78) |
; |
; |
Предположим, что и в этом случае, так же как и в гармоническом осцилляторе, вынужденные колебания происходят по гармоническому закону
G D# |
(2.79) |
2.7 ] Гармонические колебания в линейных стационарных системах 447
Проверим наше предположение, подставив функцию (2.79) в уравнение (2.78). Мы получаем
G D# ;1 G D# ;1 D#
После сокращения на множитель D# находим частотную характеристику G
G |
1 |
|
(2.80) |
1 C ; |
Итак, мы показали, что выходной сигнал фильтра, описываемый формулой (2.79), действительно представляет собой гармоническое колебание, если множитель G определяется
формулой (2.80). Соответственно |
|
|
|
A |
|
|
|||||
амплитудная G и фа- |
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
зовая # G |
характе- |
1 |
|
|
|
|
|||||
ристики имеют вид |
|
|
|
|
|
|
|
|
|||
1 |
|
, |
|
|
|
|
|
|
|
||
G |
|
|
|
(2.81) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
1 ; 2 |
|
|
|
|
|
|
|||||
|
|
|
0 |
ω |
|||||||
|
|
||||||||||
#% |
|
|
|
|
|
|
Рис. 2.19 |
||||
Амплитудная характеристика %-фильтра показана на рис. 2.19. 2. Аналогичным образом, используя закон Кирхгофа для +-фильтра (см. рис. 2.18 б) и имея ввиду, что выходной сигнал (напряжение на катушке индуктивности) 9 + ,
находим
: +:
Переходя к комплексной форме записи, получаем
1 |
|
1 |
1 |
D# |
: Re 1 |
(2.82) |
|
|
|
||||||
|
|
|
|
|
Ищем решение последнего уравнения в виде 1 G1 D#. После подстановки в уравнение (2.82) получаем
1 |
|
|
|
1 |
# |
|
|
G1 |
|
|
и 1 C D |
|
|
||
C |
|
||||||
Соответственно |
|
|
|
|
|
||
+ 1 |
|
C |
D# |
|
(2.83) |
||
C |
|
||||||
|
|
|
|
|
|
|
|
Итак, выходной сигнал представляет собой гармоническое колебание, причем частотная характеристика +-фильтра
имеет вид |
C |
|
|
|
G |
|
(2.84) |
||
C |
||||
|
|
|

448 Колебания в линейных системах [ Гл. 2
Далее находим:
|
G |
|
|
; # |
|
|
|
|
|
|
|
|
|||
|
2 2 |
|
|
||||
Мы можем сделать важный вывод, общий для всех линейных стационарных систем (систем, описываемых линейными уравнениями с постоянными коэффициентами): гармоническое внешнее воздействие возбуждает в линейной стационарной системе колебания, которые происходят по гармоническому закону с той же частотой. Этот общий вывод можно обобщить
ei t |
|
H ( ) ei t |
с помощью символического равенства |
||||
|
|
(2.85) |
|||||
L |
+ D# G D# |
||||||
|
|
|
|
||||
|
|
Рис. 2.20 |
и изобразить с помощью |
блок-схемы, |
|||
представленной на рис. 2.20.
В рассмотренных выше примерах (гармонический осциллятор, %- и +-фильтры, механический пример) мы показали, как находится частотная характеристика G , определяющая зависимость амплитуды и фазы вынужденных колебаний от частоты внешнего гармонического воздействия.
2.8. Спектральный анализ линейных колебательных систем
Рассмотрим более общую задачу: колебания гармонического осциллятора возбуждаются внешней силой, меняющейся во времени по произвольному закону 7 .
Вместо уравнения (2.59) имеем в этом случае
9 2Æ9 2 |
2 |
7 |
(2.86) |
0 |
9 0 |
|
Отличие (2.86) от (2.59) состоит в том, что в правой части последнего уравнения вместо гармонической внешней силы
0 — произвольное воздействие 7 .
Фундаментальное свойство всех линейных систем (независимо от их конкретного устройства) состоит в следующем: результат нескольких одновременных воздействий можно найти, суммируя результаты, к которым приводит каждое отдельное воздействие.
Убедимся в этом на примере гармонического осциллятора. Пусть внешняя сила описывается функцией 71 . Возникающий при этом процесс колебаний — функцией 91 . Мы имеем урав-
нение |
2Æ9 |
|
2 |
|
|
2 |
|
|
, |
(2.87) |
9 |
1 |
9 |
1 |
7 |
1 |
|||||
1 |
|
0 |
|
0 |
|
|
|
что символически запишем в виде: + 71 91 .

2.8 ] Спектральный анализ линейных колебательных систем 449
Аналогично, при внешнем воздействии 72 колебания осциллятора описываются функцией 92 , подчиняющейся урав-
нению |
|
2 |
2 |
|
(2.88) |
|
|||||
|
92 |
2Æ92 092 072 |
|||
или
+ 72 92
Как колеблется осциллятор, если внешняя сила изменяется
по закону
7 171 272 ,
где 1 и 2 — произвольные постоянные?
Искомый процесс вынужденных колебаний 9 описывается уравнением
2 |
2 |
171 272 |
(2.89) |
9 2Æ9 0 |
9 0 |
Домножив левые и правые части (2.87) и (2.88) соответственно на 1 и 2 и сложив их, убеждаемся, что искомая функция 9 может быть представлена в виде
9 191 292 |
(2.90) |
Обобщая сказанное выше на произвольную линейную систему, приходим к равенству
+ 191 292 1+ 71 2+ 72 |
(2.91) |
Итак, отклик линейной системы на линейную комбинацию внешних воздействий равен линейной комбинации откликов на каждое отдельное воздействие.
Можно обобщить (2.91), рассматривая произвольную линейную суперпозицию вида:
7 7 |
(2.92) |
1 |
|
Тогда вместо (2.91) имеем |
|
9 + 7 + 7 |
(2.93) |
Сказанное выше подсказывает путь решения общей задачи изучения колебаний линейной системы под действием произвольной внешней силы 7 .
Целесообразно представить эту силу в виде суммы (2.92) некоторых элементарных слагаемых — элементарных «кирпичиков» (в общем случае сумма может быть бесконечной).
Затем необходимо найти отклик 9 системы на каждое отдельное слагаемое 7
9 + 7 ,
15 Основы физики. Т. I
450 |
Колебания в линейных системах |
[ Гл. 2 |
и, наконец, записать искомый процесс вынужденных колебаний в виде линейной суперпозиции откликов
9 |
9 |
Мы описали суть спектрального подхода к исследованию линейных систем.
Разумеется, выбор «базиса» — 7 — тех элементарных «кирпичиков», из которых мы складываем «здание» заданной внешней силы 7 , неоднозначен. Это — вопрос физической целесообразности, он зависит от того, насколько просто можно найти реакцию системы на каждое отдельное слагаемое. Мы исследуем сейчас поведение линейных стационарных систем (т. е. линейных систем, свойства которых не меняются со временем: например, колебательный контур с постоянными +, %, или
маятник неизменной длины и массы). Мы выяснили, что по отношению к таким системам особую роль играют гармонические
функции (записанные в комплексной форме) D#. Рассматривая гармонический осциллятор, а также примеры
других линейных систем, мы убедились в том, что гармоническая внешняя сила 7 D# возбуждает в линейной системе колебания, происходящие также по гармоническому закону с той же частотой .
Символически этот результат мы записали в виде равенства (2.85) и изобразили в виде блок-схемы (рис. 2.20).
Напомним: запись (2.85) означает, что отклик линейной системы + на входной сигнал D# есть G D#.
Множитель G зависит от свойств линейной системы и называется частотной характеристикой системы (мы нашли
ее ранее для гармонического осциллятора (см. формулу (2.66),%- и +-фильтров и механической системы).
Используя математическую терминологию, можно сказать, что гармонические функции D# являются собственными функциями линейной системы +. Этот факт и отражает равенство (2.85): гармоническая функция D# преобразуется системой в гармоническую же функцию G D# (множитель G математики называют собственным значением, отвечающим собственной функции D#).
Еще раз подчеркнем, что частота в равенстве (2.85) может быть любой, при любых значениях равенство (2.85) справедливо, — и каждому значению отвечает число G — соответствующее собственное значение.
Оказывается, что гармонические функции D# (при любом ) обладают двумя важнейшими математическими свойствами, аналогичными свойствам действительных функций . Во-пер- вых, эти функции ортогональны. Смысл этого понятия состоит
