студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

1.3 ] Некоторые важные задачи сложения гармонических колебаний 391

2. Спираль Френеля — векторная диаграмма для вычисления интеграла

0

9 D,

0

Разобьем весь отрезок интегрирования 0, 0 на ! малых

Так как дуга окружности, стягиваемая суммарным вектором , имеет длину 0, то угол равен: 0 ; окончательно полу-

Как видно из векторной диаграммы (и из формулы (1.17)), величина интеграла является периодической функцией верхнего предела, изменяясь от максимального значения (равного 2*,

когда 0 $ 2* 2 1 ) до нуля при 0 2$*. Ясно, что при стремлении верхнего предела к бесконечности, величина

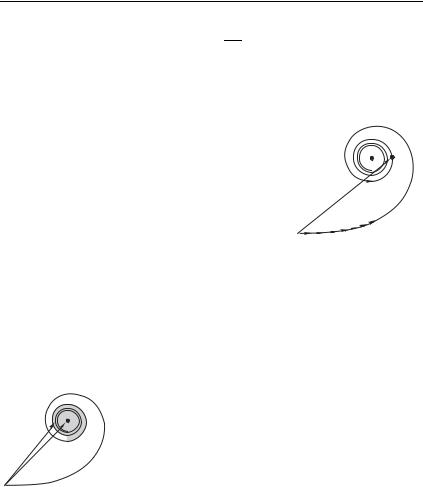
исследуемого интеграла не стремится к определенному пределу: конец суммарного вектора с ростом 0 будет двигаться по окружности радиуса 1*. Представим себе теперь, что длина каждого последующего элементарного вектора в цепочке векторов D, меньше длины предыдущего вектора; пусть, например, * является комплексным числом * * * , где * & 0. Тогда длина -го вектора есть D , , т. е. с ростом длины элементарных векторов экспоненциально уменьшаются. Ясно, что если имеется сколь угодно малое затухание амплитуд складываемых колебаний (т. е. имеется сколь угодно малое * & 0), то цепочка векторов D, при 0 образует уже не дугу окружности, а скручивающуюся спираль, фокус которой (точка, в которую эта спираль скручивается) находится в центре первоначальной окружности (рис. 1.9).

392 Кинематика колебаний [ Гл. 1

Oк интегралу вида (1.18), физически правильное его значение получается, если предполо-

перейти к пределу при * 0, в результате мы получаем ра-

венство (1.18). Изображенная на рис. 1.9 векторная диаграмма называется спиралью Френеля.

3. Спираль Корню — векторная диаграмма для вычисления интеграла

Разбив отрезок интегрирования на малые интервалы (так что) мы заменим интеграл (1.19) суммой

В отличие от предыдущего примера, здесь речь идет о сложении колебаний, фазы которых изменяются по квадратичному закону (пропорционально 2). Если в предыдущем примере угол между двумя последовательными векторами в цепочке остается постоянной величиной ( * 1 * * ), то в данном примере этот угол с ростом растет линейно:

Æ * Æ 1 2 * Æ 2 * 2 1 Æ 2

Таким образом, закручивание цепочки векторов происходит здесь неравномерно: сначала (пока * 2 2 $) кривая

очень полога и векторы D, 2 2 ) выстраиваются (почти) в прямую линию — (элементарные колебания складываются почти синфазно (рис. 1.10). Затем, при увеличении угол между двумя последовательными векторами становится весьма заметным — кривая начинает заметно скручиваться. Длина дуги первого витка 1, отмеченного на рис. 1.10 жирной линией, определяется

Если ' 1 и & 1, то концы вектора 9/ лежат в небольших окрестностях, окружающих фокусы, и значение интеграла мало меняется с изменением пределов интегрирования, поэтому имеет место следующая оценка:

окрестности одного и того же фокуса & 1, & 1, то модуль интеграла (1.22) не превышает диаметра заштрихованного круга (т. е. мал по сравнению с 90 , формула (1.21)). Этот случай изображен на рис. 1.14.

1.4. Модулированные колебания

Амплитудная и фазовая модуляции. Любой колебательный процесс, отличный от гармонического, называется модулированным колебанием. Примеры таких процессов (их осциллограммы)

приведены на рис. 1.15.

à á â

Рис. 1.15

Будем записывать модулированное колебание в виде

В отличие от гармонического колебания, здесь и — меняющиеся во времени величины. Форма записи (1.24) особенно целесообразна в том случае, когда и — медленно меняющиеся функции времени. Что означает медленность изме-

396 Кинематика колебаний [ Гл. 1

нения функций и ? Рассмотрим наряду с модулированным колебанием (1.24) гармоническое колебание

Здесь 0 — частота гармонического колебания, то есть та же самая константа, которая входит в выражение (1.24).

Рассмотрим интервал времени >, существенно превышающий период гармонического колебания 90 :

и пусть на этом интервале функции и остаются практически неизменными, причем

Итак, мы рассматриваем модулированное колебание, в котором на интервалах времени >, больших по сравнению с периодом 0 соответствующего гармонического колебания, величиныи остаются практически неизменными. В большинстве физически интересных ситуаций достаточно полагать, что сильное неравенство (1.26) выполнено, если интервал времени

> на один-два порядка превышает период колебаний 2$ 0. Такое модулированное колебание называется квазигармониче-

ским. В этом случае медленно меняющиеся величины ипринято называть амплитудой и, соответственно, начальной фазой модулированного колебания. Итак, квазигармоническое колебание можно характеризовать двумя параметрами: периодом колебаний 0 2$ 0 и временем > 0, характеризующим быстроту изменения амплитуды и (или) начальной фазы. Для описания модулированных колебаний используется

следующая терминология: говорят, что функция описывает закон амплитудной модуляции, а функция — закон фазовой модуляции.

Если 0 , то

где 0. Такое колебание называют модулированным по амплитуде.

Если 0 , то

Это — колебание, модулированное по фазе. В общем случае имеем как амплитудную, так и фазовую модуляцию, т. е. колебание вида (1.24).

Так же, как и гармонические колебания, квазигармонические процессы изображают графически в виде векторов. Если

1.4 ] Модулированные колебания 397

гармоническое колебание 90 , описываемое формулой (1.26), изображается вектором 0, имеющим фиксированную длину 0 и направление 0 (т. е. мы как бы смотрим на вращающийся с угловой скоростью 0 вектор 0 из системы координат, которая вращается с той же угловой ско-

ются (медленно, если речь идет о квазигармоническом колебании). В частности, амплитудно-модулированное колебание (1.28) изображается вектором неизменного направления 0, длина которого изменяется (рис. 1.16 а), а колебание (1.29), модулированное по фазе — вектором неизменной длины, угол наклона

которого изменяется: качания вектора на рис. 1.16 б. Аргумент косинуса в (1.29) называют фазой модулированно-

го колебания

0 ,

причем в отличие от гармонического колебания, скорость изменения фазы (величина, которую можно назвать частотой ), является функцией времени

Если выполнено условие квазигармоничности (1.26), то0, т. е. меняющаяся во времени частота мало отклоняется от частоты 0 гармонического колебания (1.25).

Отметим также, что если меняется по линейному закону, то мы получаем из (1.30)

т. е. гармоническое колебание со смещенной частотой, причем

0 при условии (1.26).

Всистеме координат, в которой гармоническое колебание

частоты 0 изображается неподвижным вектором, колебание с частотой 0 изображается вектором, медленно вращающимся против часовой стрелки с частотой , если & 0 (и по

часовой стрелке при ' 0).

Осциллограммы процессов на рис. 1.15 а, б являются примерами амплитудно-модулированных колебаний, а на рис. 1.15 в — пример колебания, модулированного по фазе.

которое показывает, что то же модулированное колебание (1.32) с законом модуляции (1.33) можно получить, сложив два гармонических колебания, немного отличающиеся по частоте: 10 и 2 0 ; 1 2 2 . Мы имеем

0 0 2 0 (1.35)

Согласно (1.35) мы получаем колебание с частотой 0, амплитуда которого 2 медленно изменяется, т. е. тот же результат. Этот эффект — возникновение колебания с ме-

няющейся амплитудой при сложении гармонических колебаний с близкими частотами называется биениями.

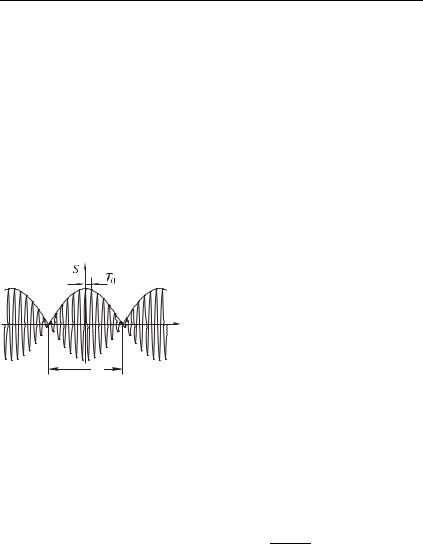
Точнее, амплитудой колебания в этом случае следует назвать величину 2 — ведь амплитуда по смыслу существенно положительная величина, она определяет «размах» колебаний. Но период функции 2 (показанной на рис. 1.17 штриховой линией) вдвое меньше периода функции 2 , поэтому период биений (интервал времени, через который повторяется максимальное значение амплитуды колебаний ) равен2$ 1 2 . Например, при разности частот слагаемых колебаний ( 1 Гц период биений равен 1 секунде.

Эффект можно получить, следовательно, не только описанным выше способом (периодически перекрывая рупор громкоговорителя), но и расположив рядом два рупора, излучающих гармонические звуковые колебания с близкими частотами (например, с частотами 440 и 441 Гц). В результате суперпозиции звуковых колебаний возникают периодические (с частотой 1 Гц) изменения громкости звука.

1.5. Спектральное разложение

Изучая колебания и волны, мы множество раз будем приходить к необходимости представлять произвольный колебательный процесс в виде суммы гармонических колебаний различных

Равенство называется спектральным разложением сигнала

9 . Оно утверждает, что можно, «правильно» подобрав частоты слагаемых гармонических колебаний, их амплитудыи начальные фазы , образовать в сумме сигнал 9 . Специальный раздел математики — Фурье-анализ — занимается математической стороной проблем, связанных с возможностью представления функций 9 в виде (1.36). Почему в качестве элементарных слагаемых во многих физических задачах оказывается целесообразно использовать гармонические колебания — об этом мы будем говорить в гл. 2. Здесь же отметим замечательные математические свойства гармонических функций.

Во-первых, гармоническое колебание частоты не может быть представлено суперпозицией гармонических колебанийлюбых других частот , какие бы коэффи-

циенты и начальные фазы мы ни старались подобрать. Математически это свойство называют ортогональностью:

функция не имееет «проекции» на любую другую функцию при , подобно тому, как вектор,

параллельный оси , невозможно представить в виде суммы векторов, параллельных осям и .

Второе важнейшее математическое свойство — единственность представления (1.36): существует единственный набор необходимых частот и единственный набор отвечающих этим частотам амплитуд и фаз , обеспечивающих представление функции 9 в виде суперпозиции гармонических функций.

Наконец, не вдаваясь в математические детали, отметим еще одно важное обстоятельство: любой физически реализуемый колебательный процесс может быть представлен в виде суммы (быть может в виде непрерывной суммы — интеграла) гармонических колебаний.

Комплексная форма спектральных разложений. Ранее мы говорили, что гармоническое колебание можно записать в комплексной форме

D # D#,

где D .

Комплексное представление часто используют и в спектральных разложениях: в качестве элементов разложения (тех элементарных кирпичиков, из которых складывается суммарный колебательный процесс 9 ) используют комплексные функции

D .

Подчеркнем, что как в случае, когда используется разложение в ряд (1.36), так и в случае, когда в качестве элементов разложения используются функции D#, мы будем говорить (если не делается специальных оговорок) о разложении в спектр реальных сигналов, описываемых действительными функция-

Мы видим, что разложения (1.36) и (1.37) будут эквивалентны, если каждому слагаемому в (1.36) поставить в соответствие два слагаемых в (1.37), т. е. каждой реальной гармонике (гармоническому колебанию с частотой ) поставить в соответствие два комплексных слагаемых, введя в (1.37) суммирование по отрицательным значениям , согласно правилу