
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf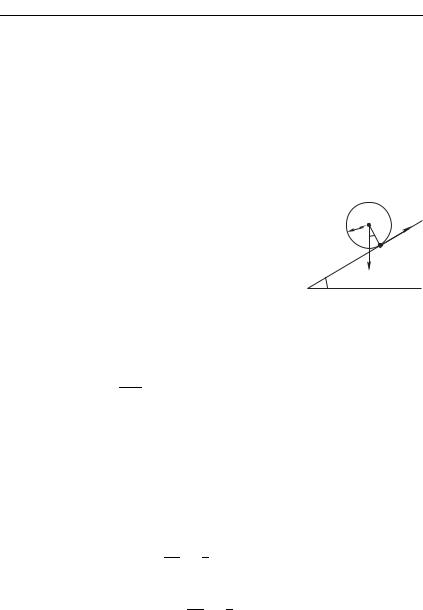
7.6 ] |
Плоское движение твердого тела |
|
|
|
141 |
|||
перемещениям, приходим к важному выводу: угловая скорость |
||||||||
при плоском движении не зависит от системы отсчета. |
||||||||
Уравнения движения, в зависимости от постановки задачи, |
||||||||
обычно пишутся либо для центра масс тела — |
|
|
|
|
||||
|
вн, |
: |
вн, |
|
|
(7.31) |
||
|
|
|
|
|
|
|
|
|
либо для мгновенной оси вращения — |
|
|
|
|
||||
|
|
|
|
|
|
|
|
(7.32) |
|
|
: вн , |
|
|
|
|||
с соответствующим пересчетом момента инерции и момента сил |
||||||||
относительно этой оси. |
|
|
|
|
|
|
||
Рассмотрим в качестве иллюстрации за- |
|
|
Ñ |
Fòð |
||||
дачу о скатывании однородного сплошно- |
|
R |
||||||
го цилиндра массы и радиуса с на- |
|
|
|
|||||
клонной плоскости, образующей с горизон- |
|
|
|
O |
||||
том угол 5 (рис. 7.17). Предполагаем, что |
|
|
|
mg |
||||
цилиндр скатывается без проскальзывания, |
|
|
|
|
||||
тогда скорость в точке равна нулю. Мгно- |
|
Рис. 7.17 |
||||||
венная ось вращения совпадает с линией |
|
|||||||
зацепления, проходящей через точку , в которой к телу прило- |
||||||||
жена сила трения. Второй закон Ньютона, с учетом направления |
||||||||
движения, целесообразно записать в проекции на наклонную |
||||||||
плоскость: |
|
|
5 тр, |
|
|
|
(7.33) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
а уравнение моментов запишем относительно мгновенной оси: |
||||||||
: |
|
|
|
1 |
2 2 5, |
(7.34) |
||
|
|
|
|
|||||
|
2 |
|||||||
|
|
|
|
|||||
(мы использовали теорему Штейнера для вычисления момента инерции относительно мгновенной оси вращения). Ни сила трения, ни реакция опоры не дают вклада в уравнение (7.34), поскольку обе они проходят через точку , а значит, их моменты относительно мгновенной оси равны нулю. Из (7.34) находим
угловое ускорение
23 # 5, следовательно, линейное ускорение равно
23 5
Далее, подставляя это выражение в (7.33), получаем
тр |
1 |
5 |
(7.35) |
|
3 |
||||
|
|
|
Таким образом, сила трения в данной задаче принимает вполне определенное значение. Но как мы знаем (см. гл. 5), оно не

142 Уравнение моментов. Динамика твердого тела [ Гл. 7
может превосходить предела #! , где # — коэффициент трения, а ! — сила реакции опоры, в нашем случае:
! 5 |
|
Таким образом, (7.35) можно выполнить лишь при условии |
|
5 ' 3# |
(7.36) |
По физическому смыслу (7.36) представляет собой условие непроскальзывания скатывающегося цилиндра.
Если цилиндр скатывается с высоты , то его конечная скорость равна
|
|
|
2 |
1 2 |
|
|
|
||
|
|
|
|||||||
кон 2 2 |
5 , |
|
4 |
|
|||||
3 |
3 |
||||||||
Убедимся, что такое значение скорости удовлетворяет закону
сохранения механической |
энергии. Согласно теореме Кёнига, |
||||||||||||||||
|
1 |
|
2 |
1 |
|
|
|
2 |
1 |
|
2 1 #2 |
|
2 |
||||
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
2 |
2 2 |
# |
||||||||||
|
|
|
|
|
|
|
|||||||||||
Элементарные вычисления дают то же самое значение кон. Возникает вопрос: как может сохраняться чисто механиче-
ская энергия при наличии заведомо ненулевой силы трения? Но дело в том, что сила трения приложена в точке , где скорость равна нулю, а потому и работы не совершает.
Таким образом, плоский характер движения столь существенно упрощает задачу о динамике тела конечных размеров, что она в принципе оказывается не намного сложнее задачи о динамике материальной точки.
Вопросы и задачи
1.Что такое момент импульса и момент силы?
2.Сохраняется ли при движении спутника по орбите его энергия, импульс, момент импульса?
3.Сохраняется ли суммарная энергия, суммарные импульс и момент импульса всех тел Солнечной системы?
4.Сколько степеней свободы у абсолютно твердого тела?
5.Что такое момент инерции твердого тела?
6.Что такое момент силы относительно оси?
7.Что такое главные оси инерции твердого тела?
8.Чему равен момент инерции тонкого однородного кольца массы и радиуса относительно оси, касательной к нему и перпендикулярной его
плоскости?
Ответ: + 2 2.
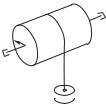
9. Однородный цилиндр массы 1 и радиуса вращается без трения вокруг горизонтальной оси под действием груза массы 2, прикрепленного к легкой нерастяжимой нити, намотанной на цилиндр (рис. 7.18). Найти угол поворота цилиндра в зависимости от времени, если при 0 0,
0.
7.7 ] |
|
|
Вопросы и задачи |
143 |
|||||
Решение. Уравнения движения для цилиндра и для груза имеют вид |
|||||||||
+ |
2 |
|
, |
2 |
2 |
|
2 , |
||
|
2 |
|
|
||||||
|
|
|
|
2 |
|
||||
где — натяжение нити, + 1 2 2 — момент инерции цилиндра. Перемещение груза и угол поворота цилиндра связаны соот-
ношением . Учитывая это соотношение и исклю- |
|
m1 |
||||||||
чая из уравнений натяжение нити , получаем: |
|
|||||||||
|
|
2 |
|
|
R |
|||||
+ 2 |
2 |
|
2 |
|
|
|
||||
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
Решение этого уравнения, удовлетворяющее начальным |
|
|
|
|||||||
условиям, имеет вид |
|
|
2 |
|
|
m2 |
||||
|
|
|
|
|
|
|
|
|||
2 1 1 2 2 |
|
|
|
|||||||
Проверьте решение по размерности и по очевидным ре- |
Рис. 7.18 |
|||||||||
зультатам в предельных случаях ( 0, |
2 0 и т. п.). |
|||||||||
|
|
|
||||||||
10. Вертикальный столб высотой |
подпиливается у основания и падает |
|||||||||
на землю, поворачиваясь вокруг нижнего основания. Определить линейную скорость его верхнего конца в момент удара о землю.
Ответ: 3 .
Ук а з а н и е : Воспользоваться законом сохранения энергии.
11. Однородный тонкий тяжелый стержень длины висит на горизонтальной оси, проходящей через один из его концов. Какую начальную угловую скорость надо сообщить стержню, чтобы он повернулся на 90Æ?
Ответ: 3 .
12. Небесное тело 1991ДА движется по вытянутой орбите, так что минимальное расстояние от него до Солнца равно радиусу орбиты Марса, а максимальное — радиусу орбиты Урана. Определите период обращения 1991ДА вокруг Солнца , если известны периоды обращения Марса 1 1,88 года и Урана 2 84 года.
Ответ: 2 |
3 2 2 3 |
2 3 3 2 |
1 |
2 . |
|
13. В 1978 г. |
у планеты Плутон обнаружен спутник — Харон. Плу- |
|
тон и Харон обращаются вокруг общего центра масс по круговым орбитам, причем расстояние между их центрами 19 640 км, а период обращения6,4 суток. Определите, какую часть массы Земли составляет суммарная масса системы Плутон–Харон. Считать известными радиус Земли 6 400 км и ускорение свободного падения на поверхности Земли.
Ответ: Пл Х З 4 2 3 2 З 0,024
Г л а в а 8
ЭЛЕМЕНТЫ МЕХАНИКИ СПЛОШНЫХ СРЕД
8.1. Упругие деформации. Закон Гука
До сих пор мы изучали условия равновесия или характер динамики либо отдельной материальной точки, либо их совокупности. Абсолютно твердое тело рассматривалось как важный частный случай такой совокупности. Теперь мы обращаемся к сплошной среде. Такое понятие используется при решении задач, которые затруднительно свести к механике материальной точки. Различие относится, конечно же, не к предмету, но к методу рассмотрения.
Когда мы говорим об абсолютно твердом теле, мы просто пренебрегаем его деформациями, полагая, что их учет приведет лишь к некоторым малым поправкам в ответе динамической задачи. То же можно сказать и о любой материальной точке, хотя в этом приближении влияние деформаций и не столь очевидно. Но избежать деформаций невозможно в принципе, и это оказывается следствием самых фундаментальных физических законов. В самом деле, представим себе абсолютно твердый стержень. Приложим к одному его концу некоторую силу, которая приведет его в движение в продольном направлении. Поскольку стержень не может деформироваться, оба его конца должны начать двигаться одновременно, но это значит, что мы транслировали воздействие (сигнал) от одного конца к другому с бесконечной скоростью. Это решительно противоречит теории относительности, поскольку по современным понятиям эта скорость должна быть конечной и не может превышать скорости света (см. гл. 10).
Описанный мысленный эксперимент лишь показывает, что никакое тело нельзя считать абсолютно твердым в абсолютном смысле, т. е. безотносительно к постановке задачи. Корректный учет деформаций и механических напряжений в целом составляет предмет обширной и довольно сложной области механики, во многих отношениях смыкающейся с физикой твердого тела. Механика деформируемых тел имеет массу технических приложений, весьма важных в практическом отношении. В нашем же курсе мы вынуждены ограничиться наиболее простыми и фундаментальными положениями этой науки.
Во-первых, мы ограничимся рассмотрением упругих, или, что то же, обратимых, деформаций. Тем самым мы оставляем за
8.1 ] |
Упругие деформации. Закон Гука |
145 |
рамками нашего курса эффекты пластичности и механического разрушения. Упругие деформации, по определению, исчезают после снятия вызывающих их напряжений, то есть не сопровождаются ни диссипацией, ни перестройкой структуры вещества. Строго говоря, абсолютно упругих деформаций не бывает, но в массе практически интересных случаев мы с очень хорошей
точностью можем использовать такое приближение.
Во-вторых, мы определим твердое тело так, как принято определять его в физике, а именно — как кристаллическое состояние. В бытовом понимании (и даже в механике, пока и
поскольку мы не касаемся проблемы деформаций) твердыми телами можно считать также переохлажденные жидкости (стекла). Но их свойства с точки зрения материаловедения весьма нетривиальны, например, под нагрузкой они могут течь, только очень медленно. Еще большее своеобразие обнаруживает высокополимерная фаза. Но мы ограничимся рассмотрением упругих свойств кристаллов.
В-третьих, мы не будем касаться монокристаллов, а займемся исключительно поликристаллическими телами — к таковым от-
носятся, например, все обычные изделия из различных металлов. Они не демонстрируют упорядоченности структуры, характерной для монокристаллов, но в кажущемся хаосе расположения элементарных монокристалликов сохраняются некоторые присущие им свойства.
По отношению к деформациям монокристалл и поликристалл могут быть весьма различны. Например, предел упругости мо-
нокристалла Al составляет примерно 40 Н/см2, а у технического
алюминия тот же параметр равен 104 Н/см2. Если же говорить об упругих свойствах, то для монокристалла их можно характеризовать как минимум тремя константами — в случае кубической решетки, — а для более сложных кристаллов это число достигает 21. Упругие свойства поликристалла описываются всего двумя независимыми константами.
Простейшим и важнейшим законом, которому подчиняются упругие деформации, является закон Гука. В изначальном виде он формулировался предельно просто: при растяжении или сжатии твердого стержня малое изменение его длины оказывается пропорционально приложенной силе:
|
(8.1) |
|
|
При этом величина силы должна быть много меньше некоторого предела упругости 0, за которым начинаются необра-
тимые деформации. Существенно, что коэффициент — один и тот же при растяжении и сжатии стержня. Однако закон Гука в виде (8.1) выглядит слишком неуниверсальным; получается,
146 |
|
Элементы механики сплошных сред |
[ Гл. 8 |
|
что коэффициент должен определяться особо для каждого |
||||
отдельного тела, и даже для воздействия на одно и то же тело |
||||
в разных направлениях. Привести его к более конструктивной |
||||
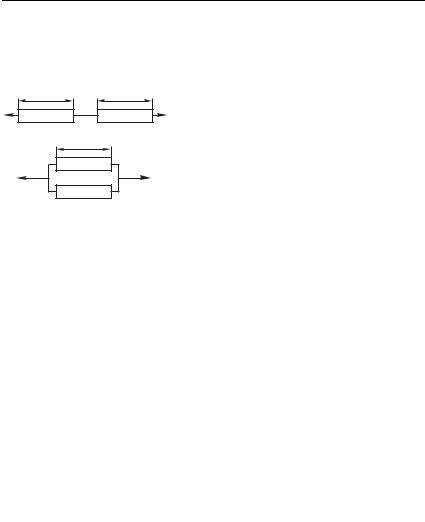
форме нам поможет рис. 8.1. Возьмем два одинаковых стержня |
||||
|
|
|
длины с поперечным сечением 9 |
|
|
l |
l |
и растянем их силой , сцепив |
|
F |
|
F |
последовательно, |
как показано на |
S |
S |
рис. 8.1 а. Каждый стержень растя- |
||
à |
|
|
||
l |
|
гивается силой , каждый удлиня- |
||
|
|
|||
|
S |
|
ется на , а вместе они удлиняются |
|
2F |
2F |
на 2 . Отсюда ясно, что , и |
||
|
S |
|
(8.1) можно переписать следующим |
|
á |
|
образом: |
|
|
|
|
|
||
|
Рис. 8.1 |
|
|
|
|
|
|
|
1 |
Если теперь сцепить стержни параллельно (рис. 8.1 б) и приложить силу 2 , каждый стержень снова растягивается силойи удлиняется на . Представим систему, изображенную на рис. 8.1 б, как стержень длины с поперечным сечением 29. Отсюда следует, что растяжение задается не силой как таковой, но отношением силы к площади сечения:
; |
|
(8.2) |
( |
|
|
Величина ; в механике деформируемых тел называется напряжением и измеряется в Н/м2 (в технике часто пользуются
внесистемной единицей кгс/см2). В телах сложной формы и при сложных нагрузках естественно использовать определение
; |
При этом величина ; в общем случае характери- |
||
зуется двумя векторами: ориентацией площадки |
и вектором |
||
силы |
. |
|
|
С учетом изложенных выше соображений закон Гука приоб- |
|||
ретает окончательный вид |
|
|
|
|
< |
- , |
(8.3) |
|
|
* |
|
где < называется деформацией, а величина - теперь уже просто константа вещества, которую называют модулем Юнга (по имени английского ученого Т. Юнга (1773–1829)).
Линейность закона (8.3) отражает всего лишь тот факт, что в разложении функции общего вида
; -< - <2 - <3
первый член при упругих деформациях доминирует, и таким образом, существенной оказывается только одна константа вещества. Но как следствие продольной деформации, может из-
8.1 ] |
Упругие деформации. Закон Гука |
147 |
мениться и поперечный размер тела. Опыт показывает, что и этот закон для поликристаллических веществ в пределах упругих деформаций оказывается линейным, причем знак поперечной деформации противоположен знаку продольной:
< |
|
1 |
1< |
(8.4) |
|
|
|
|
Константа вещества 1 называется коэффициентом Пуассона (по имени французского ученого С. Пуассона (1781–1840)). Важно отметить, что поперечная деформация вызвана продольным напряжением и сама дополнительных напряжений не вызывает.
Работа, совершенная при растяжении или сжатии образца, зависит исключительно от продольной деформации, в силу соот-
ношения
Æ
Совершенная работа запасается в виде энергии упругой деформации, которая освобождается при снятии нагрузки,
|
|
1 |
2 |
||
|
|
|
|
||
, ;9 |
|
( |
; |
2 -* |
|
* |
2 |
||||
0 |
0 |
|
|
||
Эта энергия распределена по всему объему деформированного тела, что дает основание ввести плотность энергии упругой деформации
= |
1 |
-2 |
|
1 |
;< |
1 |
-< |
2 |
(8.5) |
2 |
* |
2 |
2 |
|
|||||
|
|
|
|
|
|
Оказывается, две константы — - и 1 — в линейном случае, характерном для упругих деформаций поликристаллов, исчерпывающим образом описывают упругие свойства вещества, то есть
линейный отклик на любое воздействие, мо- |
|
|
|
|
|
|
||
жет быть выражен через эти две постоян- |
|
z |
|
|
P |
|||
|
|
|
||||||
|
|
|
||||||
ные. Нам предстоит убедиться в этом на ряде |
|
|
|
|
||||
|
|
|
|
|
|
|||
хрестоматийных примеров. Первый пример — |
|
|
|
|
|
P |
||
|
|
|
|
|
||||
|
|
|
|
|
||||
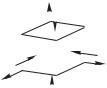
всестороннее сжатие твердого тела. Введем |
|
|
|
|
|
|||
P |
|
|
|
|
|
|||
понятие давления — нагрузки, действующей |
|
|
|
|
|
y |
||
|
|
|||||||
по нормали к поверхности тела — |
x |
|
|
P |
||||
|
|
|||||||
|
|
|
|
Рис. 8.2 |
||||
( |
|
|
|
|
|
|
|
|
Как известно, эта величина измеряется в |
паскалях: |
|
|
1 Па |
||||
1 Н/м2. Для облегчения последующих вычислений рассмотрим тело, имеющее форму параллелепипеда (рис. 8.2). Для одной продольной и двух поперечных деформаций, обусловленных

148 Элементы механики сплошных сред [ Гл. 8
продольным напряжением вдоль каждой из его осей, получаем
по оси |
< |
|
; |
< , < 1 |
|
|
, |
|||
* |
* |
|||||||||
по оси |
< |
|
; |
< , < 1 |
|
|
, |
|||
* |
* |
|||||||||
по оси |
< |
|
; |
< , < 1 |
|
|
||||
* |
* |
|||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
< |
< < |
|
|
1 21 |
|
|
(8.6) |
|||
* |
|
|
||||||||
Соответственно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Æ" Æ 2 Æ |
|
|
|
|
||||||
" |
|
|
|
|
|
3 |
|
|
|
|
|
< |
< < |
1 21 (8.7) |
|||||||
|
* |
|||||||||
При всестороннем сжатии обязательно должно быть Æ2 ' 0, в противном случае тело было бы неустойчиво по отношению к неограниченной самодеформации. Действительно, пусть
# & 0 и в результате случайной температурной флуктуации объем тела увеличился, это эквивалентно тому, что мы подвергли тело сжатию. Но увеличение объема приводит к еще большему увеличению давления, т. к. 8 1 2 2 & 0 и т. д. Отсюда следует универсальное ограничение
0 ' 1 ' |
1 |
|
(8.8) |
|
2 |
||||
|
|
|
Опыт показывает, например, что у поликристаллов 1 4 ' 1 '1 2, а для пористых тел 1 0.
8.2.Сдвиг и кручение
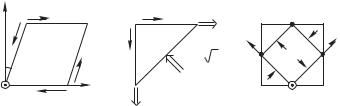
Вотличие от растяжения и сжатия, деформация сдвига
вызывается |
касательными напряжениями |
(рис. |
8.3 а). |
Пусть |
|
> |
|
— касательное напряжение |
( — |
сила, |
парал- |
лельная поверхности пробного кубика). Следствием деформации будет угол перекоса 5. При условии его малости связь между воздействием и откликом должна быть линейной —
5 ?>, |
(8.9) |
где коэффициент ? именуется модулем сдвига, а все соотношение (8.9), как и (8.3), — законом Гука.
Для равновесия деформированного кубика к нему одновременно с касательным напряжением > должно быть приложено еще одно, равное и противоположно направленное (показано
8.2 ] |
Сдвиг и кручение |
149 |
на рис. 8.3 а штрихованной стрелкой), а также дополнительная пара сил, уравновешивающая момент этих сил, показанная на рис. 8.3 а точечными стрелками. Два верхних напряжения
y |
|
|
|
|
|
|
|
c |
|
|
|
B |
C |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
dS |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS |
2 |
b |
|
|
|
d |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
x |
dS |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à |
|
á |
|
|
|
â |
|
|
Рис. 8.3
обеспечиваютcя непосредственно воздействием, нижние — реакцией опоры. Рассмотрим равновесие уголка % (рис. 8.3 б). Из построения равновесия сил, действующих на уголок (>
вдоль граней и %, > 2 — по биссектрисе угла %), следует, что на поверхности возникает такое же напряжение >, но уже не касательное, а нормальное. Как следствие, внутри деформируемого кубика можно выделить кубик (рис. 8.3 в), который подвергается растяжению по оси @ и сжатию по оси 0. Далее каждому способу рассмотрения упругой деформации будет удобно поставить в соответствие свою плотность энергии. Во-первых, в соответствии с рис. 8.3 а,
|
1 |
|
|
|
|
|
1 |
> |
|
|
|
5 = |
|
|
|
|
1 |
> |
|
5 |
.2 |
|
|
|
|||||
2 |
|
2 |
|
|
|
" |
|
2 |
|
2/ |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
С другой стороны (см. рис. 8.3 в), |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
< < |
|
. |
1 |
. |
|
|
|
|
2 > |
|
0 1 |
= > < |
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
* |
|
* |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
.2 |
|
> |
2 |
1 ! |
? |
|
* |
|
|
|
|
|
|
(8.10) |
|||||||||
|
|
|
|
|
|
2/ |
|
|
|
|
|
1 ! |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Итак, модуль сдвига удается выразить через две ранее введенные упругие константы.
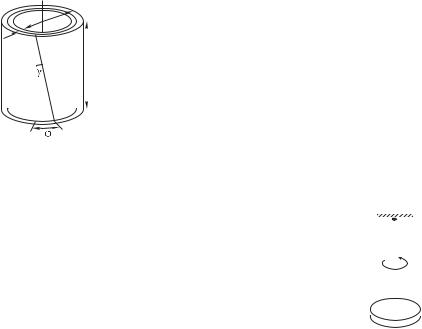
Рассмотрим деформацию кручения (рис. 8.4). Пусть к цилиндру радиуса с закрепленным основанием приложен крутящий момент . Если при этом свободный конец прокручивается на угол , то линейный закон, аналогичный (8.3), имеет вид
7 , |
(8.11) |
где 7 именуется модулем кручения. Рассмотрев деформацию трубочки радиуса и толщины Æ , нетрудно убедиться, что для нее кручение эквивалентно деформации сдвига, причем угол
150 |
|
|
|
|
Элементы механики сплошных сред |
[ Гл. 8 |
||||
сдвига тривиальным образом связан с , |
|
|
||||||||
|
|
|
|
|
|
|
5 , |
|
|
|
|
r |
R |
|
|
|
где — длина образца. Вклад в полный момент |
||||
|
|
|
|
|||||||
|
|
|
|
|
|
от нашей трубочки равен |
|
|
||
|
|
|
|
|
h |
Æ > 2$Æ , |
где |
|
> ?5 ? # |
|
|
|
|
|
|
|
Соответственно, для сплошного цилиндра |
||||
|
|
|
|
|
|
|
2/ |
|
/4 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Æ |
3 |
|||
|
|
|
|
|
|
|
|
2 7 |
||
|
|
|
|
|
|
|
|
|||
|
Рис. 8.4 |
0 |
|
|
|
(8.12) |
||||
Таким образом, модуль кручения однородного стержня равен
$?4 2 , а для тонкой трубочки — 2$ 3Æ ?. Мы вновь |
|||||
убедились в том, что линейный отклик на внешнее |
|
|
|
|
|
воздействие может быть выражен исключительно че- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рез модуль Юнга и коэффициент Пуассона. Инте- |
|
|
|
|
|
ресным следствием закона (8.11) оказывается соот- |
|
|
|
|
|
ношение для так называемых крутильных колебаний. |
|
|
|||
|
|
|
|
|
|
Пусть массивное симметричное тело радиуса с мо- |
|
|
|
|
|
ментом инерции : подвешено на проволоке длины и |
|
|
|
I |
|
радиуса с модулем кручения 7 (рис. 8.5). Уравнение |
|
|
|
|
|
|
|
|
|
|
|
моментов (7.13) для этого случая приводится к виду |
|
|
|
|
|
: 7, |
Рис. 8.5 |
||||
а это уравнение типа (4.18), решение которого хорошо известно:
|
0 |
B , |
где 2 2 |
/#4 |
|
|
|
+ |
2 |
|
8.3. Течение идеальной жидкости. Уравнение непрерывности
В отличие от твердых тел жидкости и газы с точки зрения механики являются веществами текучими. Но если в твердых телах пластичность неотделима от диссипации, то в случае текучей среды диссипацией при рассмотрении многих важных
процессов и явлений можно пренебречь. Такой подход называется приближением идеальной жидкости (заметим, что во
многих случаях приближение идеальной жидкости описывает
и динамику течения газа). Далее, очень многие практически важные задачи допускают представление о несжимаемой жид-
кости. Это понятие вошло в обиход и нередко используется в технических приложениях, но надо отдавать себе отчет в том, что сжимаемость жидкости, если понимать ее в контексте гл. 8.1,
