
Физика для бакалавра Часть 2
..pdf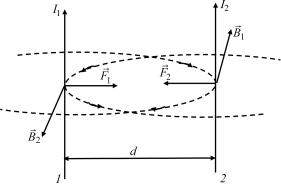
Рис. 17.10
По закону Ампера (17.13) находим силу, с которой проводник 1 действует на проводник 2:
F |
= I |
2 |
B l |
sin |
α = μμ0 |
2I1I2l2 , |
|
2 |
|
1 2 |
|
4π |
d |
|
|
|
|
|
|
|
|
||
где l2 – длина проводника 2, угол α = π |
(см. рис. 17.10). |
|
|||||
|
|
|
|
|
2 |
|
|
Аналогично находим силу F1, действующую со стороны |
|||||||
проводника 2 на проводник 1: |
|
|
|
||||
F |
= I B l sin |
α = μμ0 |
2I1I2l1 . |
|
|||
1 |
|
1 |
2 1 |
|
4π |
d |
|
|
|
|
|
|
|
||
В частном случае, когда l1 = l2 = l, F1 = F2 = F, |
|
||||||
|
|
|
F = μμ0 2I1I2l |
. |
(17.15) |
||
|
|
|
|
4π d |
|
|
|
Из рис. 17.10 следует, что при одинаково направленных токах параллельные проводники притягиваются. (Предлагаем самостоятельно убедиться, что в случае токов противоположного направления проводники отталкиваются.)
Закон взаимодействия параллельных токов (17.15) и закон Ампера (17.13) лежат в основе определения единиц измерения
21

электромагнитных величин в Международной системе единиц (СИ), в которой в качестве основной единицы электромагнитных величин принимается единица измерения силы тока 1 А (ампер). За единицу силы тока ампер (А) принимается сила та-
кого постоянного тока, при прохождении которого по двум параллельным прямолинейным проводникам бесконечной длины, находящимся в вакууме на расстоянии 1 м друг от друга, сила электромагнитного взаимодействия проводников равна 2·10–7 Н на каждый 1 м длины проводника. С помощью этого определе-
ния ампера и формулы (17.15), в которой I1 = I2, можно найти числовое значение магнитной постоянной μ0:
μ |
0 |
4πFd |
= 4π 107 |
H |
= 4π 107 |
В с |
, |
|
2I 2l |
A2 |
А м |
||||||
|
|
|
|
или μ0 = 4π 107 Гн/м.
Единица измерения магнитной индукции – тесла (Tл) – определяется из формулы (17.11):
1 Тл = 1 Н/А·м = 1 Дж/А·м2 = 1 В·с/м2.
Единица измерения напряженности магнитного поля находится из формулы (17.7):
[H ] = [[RI ]] = 1А/м.
17.8. Движение зарядов в магнитных полях. Сила Лоренца
Можно убедиться на опыте (опыт Иоффе), что магнитное поле действует не только на проводник с током, но и на отдельные движущиеся заряды. Найдем выражение силы, действующей на электрический заряд, движущийся в магнитном поле. По закону Ампера на элемент тока действует сила
dF = [Idl ,B].
22
Если ток I в проводнике обусловлен движением частиц с зарядом q, то
Idl = qdnv,
где dn – число частиц в объеме проводника длиной dl; v – скорость их упорядоченного движения. Поэтому, подставив выра-
жение Idl в закон Ампера, находим
dF = qdn v,B .
Поделив обе части этого равенства на число частиц dn, получим силу Лоренца FЛ – силу, действующую на каждую движущуюся в магнитном поле заряженную частицу:
F = q[v,B |
]. |
(17.16) |
Л |
|
|
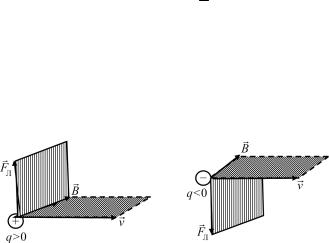
Направление силы Лоренца определяется векторным произведением [vB], т.е. она направлена перпендикулярно к плоскости, в которой лежат векторы v и B. Если заряд q положителен, направление силы совпадает с направлением вектора [vB] (рис. 17.11, а). В случае отрицательного заряда (q<0) направление векторов FЛ и[vB] противоположны (рис. 17.11, б).
F = qvBsin(B v) = qvBsinα. |
(17.17) |
Л |
|
а |
б |
Рис. 17.11
23

Сила Лоренца всегда направлена перпендикулярно скорости за-
ряженной частицы и сообщает ей нормальное ускорение. Следовательно, сила Лоренца не совершает работы, так как не изменяет модуля скорости и кинетическую энергию частицы
(поле считается постоянным).
Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярно вектору B, то сила Лоренца
постоянна по модулю FЛ = qvB, и направлена перпендикулярно линиям магнитной индукции. Отсюда следует, что сила Лоренца является центростремительной силой, под действием которой частица движется по окружности. Радиус окружности (траекторию движения частицы) определим из соотношения
mvR2 = qvB,
или
R = mv . |
(17.18) |
qB |
|
Если заряженной частицей является электрон, то формула (17.18) будет иметь вид
R = mv |
, |
(17.19) |
eB |
|
|
где е – заряд электрона.
Таким образом, зная траекторию движения электронов в известном магнитном поле B, можно вычислить отношение заряда электронакегомассе, называемоеудельным зарядом электрона.
17.9. Магнитный поток и теорема Гаусса для магнитных полей
Понятие магнитного потока играет исключительно важную роль в описании магнитных явлений, связанных с взаимодействием магнитных полей и проводников с током, а также электромагнитной индукции и т.д.
24
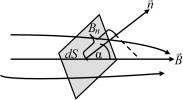
Потоком вектора магнитной индукции dФB (или магнитным потоком) сквозь малую площадку dS называется скалярная физическая величина, характеризующая интенсивность магнитного поля в данной точке пространства и чис-
ленно равная произведению величины этой площадки dS и про-
екции Вп вектора В на направление нормали n |
к площадке dS |
(рис. 17.12): |
|
dФB = B dS = Вn dS = В dSсosα, |
(17.20) |
где α – угол между В и n. Из формулы (17.20) видно, что магнитный поток – величина алгебраическая: знак dФB зависит от выбора направления нормали n к площадке dS.
Направление нормали выбирается произвольно. Тогда знак у dФB определяется знаком сos α. Магнитный поток dФB через поверхность S конечных размеров и произвольной формы равен интегралу выражения (17.20)
ФB = Bn dS = BdS cosα = B dS. |
(17.21) |
||
S |
S |
S |
|
При вычислении ФB векторы n нормалей к площадкам dS нужно направлять в одну и ту же сторону по отношению к поверхности S; например, если S – замкнутая поверхность, то векторы n должны бытьлибовсевнешними, либовсевнутренними.
В природе отсутствуют магнитные заряды, поэтому силовые линии магнитного поля замкнуты, т.е. не имеют ни начала, ни конца, что указывает на равенство нулю интеграла (17.21), взятого по произвольной замкнутой поверхности S, т.е.:
S |
S |
|
Bn dS = |
dΦ B = 0. |
(17.22) |
|
|
25 |
Выражение (17.22) представляет собой математическую запись теоремы Гаусса для вектора магнитной индукции В, кото-
рая гласит: поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю.
17.10. Теорема о циркуляции (закон полного тока)
Аналогично циркуляции вектора напряженности электростатического поля введем циркуляцию вектора магнитной ин-
дукции. Циркуляцией вектора В по заданному замкнутому кон-
туру называется интеграл
B dl = Bl dl,
где dl – вектор элементарной длины контура, направленной
вдоль обхода контура. Bl = В cos α – составляющая вектора В в направлении касательной к контуру (с учетом выбранного на-
правления обхода), α – угол между векторами В и dl .
Закон полного тока для магнитного поля в вакууме (теоре-
ма о циркуляции вектораB ): циркуляция вектора B по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром:
B dl |
n |
|
= Bl dl = μ0 Ik , |
(17.23) |
k =1
где п – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
Выражение (17.23) справедливо только для поля в вакууме, поскольку для поля в веществе необходимо учитывать молекулярные токи.
26

Продемонстрируем справедливость теоремы о циркуляции
вектора В на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного к нам (рис. 17.13).
Представим себе замкнутый кон- |
|
|
В |
|
тур в виде окружности радиусом r. |
|
|
||
|
|
|
||
В каждой точке этого контура век- |
|
|
|
|
тор В одинаков по модулю и на- |
I |
r |
|
|
правлен по касательной к окруж- |
|
|||
|
● |
|
||
ности (она является и линией маг- |
|
|
||
|
|
|
||
нитной индукции). Следовательно, |
|
|
|
|
циркуляциявектора В |
|
|
|
|
Bl dl = В dl = B2πr. |
|
Рис. 17.13 |
|
|
|
|
|
|
|
Согласно выражению (17.23) получим B2πr = μ0 I |
(в вакуу- |
|||
ме), откуда |
|
|
|
|
B = |
μ0 I . |
|
|
(17.24) |
|
2πr |
|
|
|
Таким образом, исходя из теоремы о циркуляции вектора В, получили выражениедлямагнитнойиндукцииполяпрямоготока.
Как видно из выражения (17.23), циркуляция вектора В не равна нулю. Такое поле называется вихревым.
Из выражения (17.23) можно сделать следующие выводы:
1.Магнитное поле прямолинейного тока вихревое, так как
внем циркуляция вектора В вдоль замкнутого контура не равна нулю.
2.Циркуляция вектора В вдоль замкнутого контура, охватывающего прямолинейный ток, в вакууме равна произведению магнитной постоянной на силу тока.
3.Если контур обхода не охватывает проводника с током I,
то циркуляция вектора В вдоль него равна нулю, а так как dl ≠ 0, то В = 0 вдоль этого контура.
27

4. Сила тока I и направление обхода контура связаны между собой правилом знаков: положительным в формуле (17.23) считается ток, направление которого связано с направлением обхода по контуру правилом правого винта, ток противоположного направления считается отрицательным.
Теорема о циркуляции вектора имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био–Савара–Лапласа.
17.11. Расчет магнитных полей соленоида и тороида
Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 17.14). Длину соленоида считаем во много раз больше, чем диаметр его витков, т.е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида показывает, что внутри соленоида поле является однородным, вне соленоида – неоднородным и очень слабым.
На рис. 17.14 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри его, а полем вне соленоида можно пренебречь.
Для нахождения магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис. 17.14.
Циркуляция вектора В по замкнутому контуру ABCDA, охватывающему все N витков, согласно (17.23),
28
Bl dl = μ0 NI.
АBCDA
Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной индукции и Bl = 0. На участке вне соленоида В = 0.
На участке DA циркуляция вектора В равна Bl (контур совпадает с линией магнитной индукции), следовательно,
Bl dl = Bl = μ0 NI. |
(17.25) |
DA |
|
Из (17.24) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):
B = |
μ0 NI |
. |
(17.26) |
|
l |
||||
|
|
|
||
Получаем, что поле внутри соленоида однородно. |
||||
Большое значение для практики |
|
|||
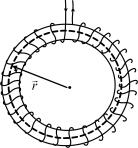
имеет также магнитное поле тороида – |
|
|||
кольцевой катушки, витки которой |
|
|||
намотаны на сердечник, имеющий |
|
|||
форму тора (рис. 17.15). Магнитное |
|
|||
поле, как показывает опыт, сосредо- |
|
|||
точено внутри тороида, вне его поле |
|
|||
отсутствует. Линии магнитной ин- |
|
|||
дукции в данном случае, как следует |
|
|||
из соображений симметрии, есть ок- |
Рис. 17.15 |
|||
ружности, центры которых располо- |
|
|||
жены по оси тороида. В качестве контура выберем одну такую окружность радиусом r. Тогда по теореме о циркуляции (17.23),
B2πr = μ0 NI ,
откуда следует, что магнитная индукция внутри тороида (в вакууме)
29
B = μ0 NI , 2πr
где N – число витков тороида.
Если контур проходит вне тороида, то токов он не охватывает и B2πr = 0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).
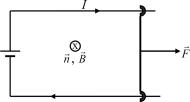
17.12.Работа, совершаемая при перемещении контура
стоком в магнитном поле
Когда контур с током находится во внешнем магнитном поле, мы будем предполагать, что оно постоянное, – на отдельные элементы контура действуют силы Ампера, а поэтому при перемещении контура эти силы будут совершать работу. Покажем, что работа, которую совершают силы Ампера при элементарном перемещении контура с током I, определяется как
δA= I dФB, |
(17.27) |
где dФB – приращение магнитного потока через контур при данном перемещении.
Доказательство этой формулы проведем в три этапа. |
|
||
|
1. Сначала рассмотрим ча- |
||
|
стный |
случай: |
контур |
|
(рис. 17.16) |
с подвижной пере- |
|
|
мычкой длины l находится в |
||
|
однородном магнитном |
поле, |
|
|
перпендикулярном плоскости |
||
|
контура и |
направленном за |
|
Рис. 17.16 |
плоскость |
рисунка. На пере- |
|
|
мычку действует амперова сила |
||
F = IlB. При перемещении перемычки вправо на dx эта сила совершает положительную работу:
δA = Fdx = IBldx = IBdS, |
(17.28) |
где dS – приращение площади, ограниченной контуром.
30
