
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf
X.2. Модельные представления интеграла столкновений
Даже упрощённый интеграл столкновений в форме Ландау достаточно громоздок. Поэтому для расчётов, в которых достаточно лишь качественно учесть столкновения, применяются модельную форму интеграла столкновений. Простейшим из них является так называемое -приближение. В этом приближении кинетическое уравнение принимает вид:
∂f |
v, f F |
∂f |
− |
f − f0 |
. |
(X.2.1) |
∂t |
∂p |
|
Здесь f0 − максвелловская функция распределения, а − время между столкновениями. Легко видеть, что интеграл столкновений не сохраняет ни числа частиц, ни полного импульса системы, но позволяет качественно проследить за ролью столкновений, например, в задачах об устойчивости слабостолкновительной плазмы.
Более аккуратное представление − это представление Батнагара - Гросса - Крука. В этом представлении интеграл столкновений имеет вид:
|
|
St − |
f − n |
. |
|
(X.2.2) |
||
|
|
|
|
|
||||
Здесь |
n − |
|
плотность |
|
плазмы, |
|||
|
m |
3/2 exp − |
m v−u 2 |
, |
u |
− |
скорость |
|
2 T |
|
|||||||
|
|
2T |
|
|
|
|
|
|
221

коллективного движения плазмы как целого.
X.3. Убегающие электроны
В связи с тем, что кулоновское сечение быстро падает с ростом относительной скорости, в плазме, помещённой в электрическое поле, наблюдается специфическое явление "убегания" электронов. Если на длине свободного пробега электрон набирает энергию, превышающую ту, которая в среднем теряется при столкновениях, то он будет в среднем ускоряться.
Упорядоченную скорость, которую набирает электрон на длине свободного побега l ne t, можно вычислить как отношение энергии, набранной в электрическом поле, к импульсу, который не сильно отличается от теплового,
|
eEl |
|
|
|
eE |
|
|
|
|
|
(X.3.1) |
|
V mvTe |
mvTene t . |
|
|
|
||||||||
Положив в |
транспортном |
сечении |
|
(X.1.23) |
||||||||
|v − v1 | vTe, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v3 |
|
|
|
|
|
|
|
|
|
|
V |
|
|
Te |
, |
|
|
|
|
|
(X.3.2) |
|
|
|
|
vc2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь vc − критическая скорость, vc |
|
|
4 e3ne |
L . |
||||||||
|
|
|||||||||||
Если vTe vc, |
т.е.E Ec |
|
|
4 e3ne |
L, |
|
|
mE |
||||
|
|
то |
основная |
|||||||||
|
Te |
|
||||||||||
масса электронов уходит в "просвист". Поле Ec называют полем Драйсера. Высокоэнергетический хвост функции распределения оказывается сильно
222
отличающимся от максвелловского даже при малом электрическом поле.
Заключение
Внастоящем пособии изложен ряд базовых вопросов теории плазмы вестма общего характера. Без их понимания невозможно изучение более специфических областей теории. В частности, невозможно понимание теории равновесия, устойчивости и переносов в неоднородной плазме, являющихся определяющими для понимания процессов, происходящих в термоядерных реакторах, основанных на разных принципах. Автор надеется во второй части пособия изложить основы теории магнитного удержания.
Взаключение автор хотел бы поблагодарить Н.К. Трофимову и С. Вафина за большую помощь при подготовке рукописи к печати.
223
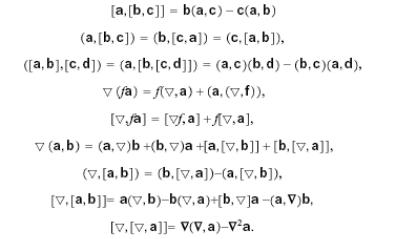
Приложение. Некоторые формулы векторной алгебры и векторного анализа
Последняя формула справедлива только в декартовых координатах.
224

Дифференциальные операторы в цилиндрической r, , z и сферической r, ,
системах координат
Список литературы
[1]Ландау Л.Д., Лифшиц Е.М., Теория поля.
[2]Дорман Л.И., Смирнов В.С., Тясто М.И. Космические лучи в магнитном поле Земли. М.:
Наука, 1971.
[3]Труханов К.А., Рябова Т.Я. , Морозов. Д.Х.
225
Активная защита космических кораблей. М.: Атомиздат, 1970.
[4]Ландау Л.Д., Лифшиц Е.М., Механика.
[5]Сивухин Д.В. // "Вопросы теорнии плазмы"/ Под ред.акад. М.А. Леонтовича. Вып 1. М.: Атомиздат, 1963. С.7.
[6]Трубников Б.А. Теория плазмы. М.: Энергоатомиздат, 1996, С. 92.
[7]Заславский Г.М. Стохастичность динамических систем, М.: Наука, 1984.
[8]Morozov D.Kh., Herrera J.J.E. Physics of Plasmas, (1995), V.2, p. 1540.
[9]Кадомцев Б.Б. // "Вопросы теорнии плазмы"/
Под ред.акад. М.А. Леонтовича. Вып.5. М.:
Атомиздат, 1967. С. 220.
[10]Ландау Л.Д., Лифшиц Е.М.. Магнитная гидродинамика.
[11]Волков Т.Ф.// "Вопросы теорнии плазмы"/ Под ред.акад. М.А. Леонтовича. Вып.4. М.: Атомиздат, 1964. С. 3.
[12]Ландау Л.Д., Лифшиц Е.М., Гидродинамика.
[13]Брагинский С.И. // "Вопросы теорнии плазмы"/ Под ред.акад. М.А. Леонтовича. Вып.1.
М.: Атомиздат, 1963. С. 183.
226
Содержание |
|
Предисловие...................................................................................... |
3 |
Введение............................................................................................. |
5 |
Глава I. Движение заряженных частиц |
|
в электрическом и магнитном полях.......................................... |
13 |
I.1. Лагранжева и гамильтонова формы описания |
|
движения. Интегралы движения |
|
в симметричных системах.......................................................... |
13 |
I.2. Движение частиц в однородных |
|
и постоянных полях.................................................................... |
20 |
I.3. Движение частиц в аксиально |
|
симметричном магнитном поле. Задача Штермера................. |
28 |
I.4. Приближенные методы расчета траекторий. |
|
Адиабатические инварианты. Дрейфовое |
|
приближение............................................................................... |
34 |
Глава II. Описание стационарного магнитного |
|
поля в ловушках............................................................................. |
50 |
II.1. Основные понятия............................................................... |
50 |
II.2. Магнитные поверхности, коэффициент запаса |
|
устойчивости, шир...................................................................... |
55 |
II.3. Устойчивость магнитных поверхностей........................... |
68 |
Глава III. Траектории частиц в токамаке................................. |
77 |
Глава IV. Плазма как сплошная среда. |
|
Кинетическое описание................................................................. |
92 |
IV.1. Заряд в плазме. Дебаевская экранировка ........................ |
92 |
IV.2. Кинетическое уравнение................................................... |
95 |
IV.3. Ленгмюровские волны...................................................... |
98 |
IV.4. Затухание Ландау............................................................ |
103 |
IV.5. Диэлектрическая проницаемость |
|
максвелловской плазмы с неподвижными ионами................ |
106 |
IV.6. Учёт движения ионов...................................................... |
112 |
IV.7. Квазилинейная теория затухания Ландау...................... |
116 |
Глава V. Уравнения магнитной гидродинамики. |
|
Метод моментов............................................................................ |
122 |
V.1. Нулевой момент (уравнение непрерывности) ................ |
123 |
V.2. Первый момент (аналог уравнения |
|
Навье-Стокса)............................................................................ |
127 |
V.3. Второй момент (уравнение для температуры) ............... |
134 |
227
V.4. Одножидкостная гидродинамика.................................... |
136 |
V.5. Теорема вмороженности.................................................. |
140 |
Глава VI. МГД-волны и течения в идеально |
|
проводящей плазме...................................................................... |
144 |
VI.1. МГД-волны малой амплитуды в холодной плазме ...... |
144 |
VI.2. Тангенциальные разрывы............................................... |
153 |
VI.3. Вращательные разрывы.................................................. |
158 |
Глава VII. Ударные волны......................................................... |
166 |
VII.1. Общие соотношения...................................................... |
166 |
VII.2. Слабые ударные волны.................................................. |
169 |
VII.3. Ударные волны в слабых полях.................................... |
171 |
VII.4. Генерация магнитного поля |
|
при турбулентном движении................................................... |
175 |
Глава VIII. Нелинейные волны в плазме................................ |
177 |
VIII.1. Простые волны.............................................................. |
177 |
VIII.2. Нелинейное распространение ионного звука............. |
179 |
VIII.3. Нелинейные МГД-волны.............................................. |
181 |
VIII.4. Волны на мелкой воде.................................................. |
182 |
VIII.5. Волны в средах со слабой дисперсией. |
|
Уравнение Кортевега-де Вриза. Солитоны............................ |
185 |
Глава IX. Электромагнитные волны в плазме....................... |
191 |
IX.1. Электромагнитные волны |
|
в незамагниченной плазме....................................................... |
191 |
IX.2. Электромагнитные волны |
|
в замагниченной плазме........................................................... |
195 |
IX.3. Пучковая неустойчивость............................................... |
207 |
IX.4. Двухпотоковая неустойчивость ..................................... |
210 |
Глава X. Столкновение в плазме .............................................. |
211 |
X.1. Интеграл столкновений в форме Ландау........................ |
211 |
X.2. Модельные представления интеграла |
|
столкновений............................................................................. |
221 |
X.3. Убегающие электроны ..................................................... |
222 |
Заключение.................................................................................... |
223 |
Приложение. Некоторые формулы векторной |
|
алгебры и векторного анализа....................................................... |
224 |
Список литературы ........................................................................ |
225 |
228
