Морозов Введение в теорию горячей плазмы Ч.1 2011

довольно часто. В частности, нелинейные дрейфовые волны и атмосфера Юпитера описываются одинаковыми уравнениями, а зональные течения (горизонтальные полосы) и Большое красное пятно (рис. 3) аналогичны зональным течениям и солитону в токамаке.

Рис.3. Юпитер. В направлении на 4 часа видно Большое

красное пятно.

Естественно, что в небольшом пособии невозможно даже вкратце изложить все аспекты теории в столь различных ее приложениях. Поэтому

11

автор ставил перед собой значительно более скромную задачу: изложить основы теории сравнительно разреженной плазмы, характерной для установок магнитного удержания и ряда задач астрофизики. Не рассматриваются квантовые эффекты в плазме, неидеальная плазма, релятивистские эффекты рассматриваются лишь в приложении к движению отдельных частиц. Мне казалось важным научить читателя языку теории плазмы, чтобы он впоследствии мог сам читать научную литературу, рассказать о наиболее полезных математических приемах исследования, которые часто опускаются не только в журнальных статьях и монографиях, но даже в знаменитом многотомном курсе Ландау. Последний, несмотря на все его достоинства, все же труден для студентов.

В первую часть пособия вошли теория движения заряженных частиц в электрических и магнитных полях (с учетом релятивизма), геометрия магнитного поля в простейшей форме, кинетическое описание плазмы, получение уравнений магнитной гидродинамики из кинетического уравнения, волны в однородной плазме, линейное и квазилинейное затухание Ландау, а также ряд нелинейных явлений.

12

Глава I. Движение заряженных частиц в электрическом и магнитном полях

I.1. Лагранжева и гамильтонова формы описания движения. Интегралы движения в симметричных системах.

Мы будем рассматривать движение заряженных частиц в электрических и магнитных полях для релятивистского случая. Естественно, что такие частицы присутствуют в космической плазме. Но даже в токамаках, где температура плазмы существенно ниже релятивистского уровня, возникают группы электронов, ускоренных до релятивистских скоростей.

Уравнения движения заряженной частицы в декартовой системе координат хорошо известны, и задача в простейшем случае однородных полей решается достаточно просто. Однако электрические и магнитные поля как в астрофизических объектах, так и в лабораторных установках, как правило, неоднородны. Поэтому для упрощения задачи полезно перейти от декартовых к обобщенным каноническим переменным, записав уравнения движения в лагранжевой или гамильтоновой форме.

Как известно, лагранжева форма уравнений

13

имеет вид:

Здесь qi – обобщенная координата, а точка над буквой означает производную по времени. Функцию L называют функцией Лагранжа, или лагранжианом. Как известно, для релятивистской заряженной частицы в электромагнитных полях она имеет вид (см. напр. [1] :

Здесь A − векторный потенциал магнитного поля, − скалярный потенциал поля электрического.

Величина

называется обобщенным импульсом частицы. Легко убедиться, что в нерелятивистском случае функция Лагранжа сводится к разности кинетической и потенциальной энергий плюс член, описывающий взаимодействие частицы с магнитным полем.

В гамильтоновой форме уравнения движения принимают следующий вид:

14

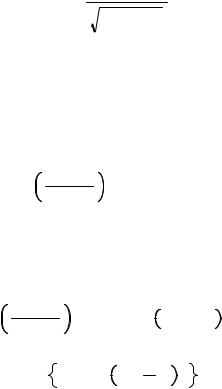
гамильтониан

Гамильтониан в нерелятивистском случае сводится к сумме кинетической и потенциальной энергий. Для того, чтобы производить вычисления с помощью уравнений (I.1.4), скорость в гамильтониане необходимо выразить через обобщенные координаты и импульсы.

С помощью (I.1.3) выразим обычный кинематический импульс p через обобщенный импульс P и подставим его в (I.1.6) . В результате находим:

Использование обобщенных координат и импульсов позволяет сразу находить некоторые интегралы движения в случае явной или скрытой симметрии. Из уравнений (I.1.1) или (I.1.2) видно, что если векторный потенциал магнитного поля и скалярный потенциал электрического одновременно не зависят от какой-либо

15

обобщенной координаты q, то соответствующий обобщенный импульс не зависит от времени, dP/dt 0.

В качестве примера можно привести движение частицы в поле магнитного диполя. Поле магнитного диполя в сферической системе координат (r, , , помещенного в начало координат, может быть описано одной компонентой векторного потенциала

интегралом движения. Чтобы получить эту величину в явном виде, надо выразить компоненты скорости через обобщенные координаты и их

16

Покажем, что уравнения (I.1.1) в декартовой системе координат приобретают привычный вид. Правая часть уравнения (I.1.1) - это просто градиент лагранжиана:

∂∂Lr L ec A V − e .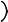

Градиент скалярного произведения приводится к виду

A, V A, V V, A

A, , V V, , A .

Первый и третий члены равны нулю, т.к. в декартовых координатах компоненты скорости и координаты – независимые переменные. Таким образом,

С другой стороны,

Полную производную по времени можно преобразовать следующим образом:

Приравнивая (I.1.11) к (I.1.12), с использованием

(I.1.13), получаем:

17

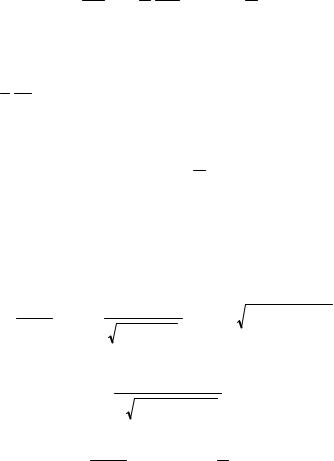
ddtp − ec ∂∂At − e ec V, H .

.

Учитывая, что электрическое поле выражается через электростатический и векторный потенциалы

e ∂A -e ≡ eE, видим, что уравнение движения

c ∂t

(I.1.1) в декартовой системе координат имеет хорошо знакомый вид:

Хорошо известно, что в нерелятивистском случае стационарное магнитное поле не меняет энергии частицы. Покажем, что это утверждение остается справедливым и в релятивистском случае. Действительно,

dEdtkin eE V ec V, H V.

Очевидно, что последний член равен нулю. Таким образом, в стационарном магнитном поле кинетическая энергия является в отсутствие электрического поля интегралом движения. В

18

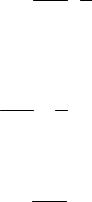
переменном магнитном поле всегда присутствует индукционное электрическое поле, и кинетическая энергия не сохраняется.

Задача

Найти функции Лагранжа и Гамильтона в нерелятивистском приближении.

Решение

Разлагая выражение (I.1.2) в ряд по отношению V/c, с точностью до членов V/c 2, имеем:

L −mc2 mV2 2 ec A V −e

Так как функция Лагранжа определена с точностью до постоянной, член mc2 можно отбросить. В результате получаем:

L mV2 2 ec A V − e .

Аналогичным образом для гамильтониана (формула I.1.6)) получаем:

H mV2 2 e .

19

1.2. Движение частиц в однородных и постоянных полях

Рассмотрим простейший случай движения релятивистской частицы в постоянном однородном электрическом поле. Будем использовать декартову систему координат. Пусть поле E const направлено вдоль оси х, а начальный импульс p0y – вдоль оси y. Уравнения движения сводятся к следующей системе:

Интегрируя один раз по времени, имеем:

Для того, чтобы получить зависимость координаты х от времени, воспользуемся выражением для кинетической энергии:

Интегрируя это выражение по времени, получаем зависимость координаты хот времени:

20