
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf
связывает частоту и волновой вектор и позволяет вычислить фазовую и групповую скорости волны.
Проинтегрируем правую часть уравнения
(IV.3.6) по частям.
|
|
1 |
|
|
|
|
∂ |
1 |
|
|
|||
|
|
|
|
|
|
|
|||||||
k |
f0 |
|
− − |
dpf0e |
|
. (IV.3.7) |
|||||||
− |
kp |
i |
∂p |
|
− |
kp |
i |
||||||
|
|
m |
m |
|
|||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
Первый член в правой части (IV.3.7) обращается в ноль в силу того, что функция распределения обращается в ноль на p . Окончательно имеем:
|
4 e2 |
|
|
1 |
|
|
|
|
1 |
dpf0e |
|
|
|
. |
(IV.3.8) |
||
m |
− |
kp |
i |
2 |
||||
|
|
− |
m |
|
|
|
Пусть равновесная функция распределения электронов − быстро спадающая с характерным масштабом v . Рассмотрим высокочастотные возмущения, kv . Тогда подынтегральное выражение можно разложить в ряд:
|
|
1 |
|
|
|
|
|
|
≈ |
1 |
|
− 2 |
kp |
3 |
k2p2 |
. |
|
|
|
||||
|
|
kp |
|
|
|
|
|
|
2 |
m 3 |
|
|
|
|
|
||||||||
|
− |
i |
2 |
|
|
|
|
|
m2 4 |
|
|
|
|||||||||||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Интеграл в правой части (IV.3.8) можно |
|||||||||||||||||||||||
представить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
kp |
|
|
2 |
2 |
|
||||
так: dpf0e |
|
|
|
|
≈ |
dpf0e |
|
|
− 2 |
|
3 |
k p |
|
|
|||||||||
|
|
|
|
2 |
2 |
|
3 |
2 |
4 |
|
|||||||||||||
|
|
− |
kp |
i |
|
|
|
|
|
|
|
|
m |
m |
|||||||||
− |
m |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
По ранее сделанному предположению средняя скорость плазмы в невозмущённом состоянии равна нулю. Это значит, что функция f0e − чётная. Следовательно, второй член в скобках при
101
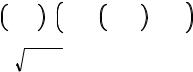
интегрировании выпадает. Окончательно получаем:
1 |
|
p 2 |
1 3 |
k |
2 |
p2 . |
(IV.3.9) |
||
|
|
|
m |
|
|||||
|
|
|
|
|
|||||
Здесь p |
|
|
4 ne2 |
называется |
плазменной |
(в |
|||
|
m |
||||||||
данном случае электронной плазменной) или ленгмюровской частотой. Угловые скобки означают усреднение с невозмущённой функцией распределения. Решение дисперсионного уравнения в нулевом приближении даёт:
p. |
(IV.3.10) |
Фазовая скорость vph при этом определяется
выражением
vph |
|
|
p |
, |
(IV.3.11) |
k |
|
||||
|
|
k |
|
||
а групповая − выражением
vgr |
∂ |
0. |
(IV.3.12) |
|
∂r |
||||
|
|
|
Плюс-минус здесь означает, что волна может бежать как в положительном, так и в отрицательном направлении.
В следующем приближении во втором члене в скобках в выражении (IV.3.9) можно положитьр. Тогда приближённо получаем :
102

|
|
3 |
|
k |
2 |
2 |
|
|
|
p |
1 |
|
p |
|
|
(IV.3.13) |
|||
2 |
|
m p |
|
p 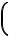 1 32
1 32 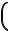 kp
kp  2 v2
2 v2 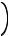 .
.
Вэтом приближении групповая скорость уже не
равна нулю,
vgr 3 |
r v2 |
. |
(IV.3.14) |
p |
Если невозмущённая функция распределения
близка к максвелловской, то средний квадрат скорости, а вместе с ней и групповая скорость пропорциональны температуре плазмы, а точнее, электронной температуре.
Рассмотренные волны называются ленгмюровскими волнами.
IV.4. Затухание Ландау
Познакомимся теперь с одним из интереснейших явлений в физике плазмы − затуханием Ландау. Мы привыкли к тому, что затухание колебаний и волн в среде связано с превращением энергии волны в тепло с помощью столкновений. Однако в плазме волна затухает за времена, много меньшие времени между
103

столкновениями, т.е. имеет место бесстолкновительное затухание. Нельзя сказать, что столкновения не играют здесь никакой роли, они обеспечивают механизм выхода частицы из резонанса с волной, могут быть как угодно редкими и из окончательного результата выпадают.
Вернёмся к исходному дисперсионному уравнению (IV.3.6), которое перепишем так:
|
4 e2 |
|
|
∂f0e |
|
|
|
1 |
|
|
|
|
|
dp |
|
|
|
|
|
. |
(IV.4.1) |
k |
∂p |
|
kp |
− 1 i |
||||||
|
− |
|
|
|
m |
|
||||
|
|
|
|
|
|
|
|
|
|
Здесь ≡ . Видно, что при → 0 знаменатель в подынтегральной функции обращается в ноль и не позволяет непосредственно вычислить интеграл. Однако можно воспользоваться предельным соотношением из теории обобщённых функций:
lim |
1 |
|
|
P z i z . |
(IV.4.2) |
||||
z − i |
|||||||||
→0 |
|
|
|
|
|
||||
Здесь z − дельта-функция Дирака. Это |
|
||||||||
выражение надо понимать так, что если под знаком |
|
||||||||
интеграла стоит дробь |
1 |
, |
то при → 0 следует |
|
|||||
z−i |
|
||||||||
вычислить интеграл в смысле главного значения, |
|
||||||||
подставив в него 1/z и прибавить к нему интеграл, в |
|
||||||||
котором вместо дроби |
|
|
1 |
|
|
подставлена функция |
|
||
|
z−i |
|
|||||||
i z . таким образом, интеграл в правой части (IV.3.6) можно представить так:
104
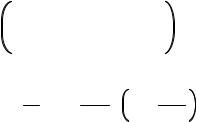
|
|
∂f0e |
|
|
|
|
1 |
|
|
|
|
|
|||||||
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
. |
(IV.4.3) |
||||
|
|
∂p |
|
|
kp |
|
− −i |
||||||||||||
|
− |
|
|
|
m |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
∂f0e |
1 |
|
|
|
|||||||||
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∂p |
|
|
kp |
|
− 1 |
||||||||||
|
|
− |
|
|
|
|
|
|
|
m |
|
VP |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
i 1 dp ∂f0e 1 − kp
∂p m
−
Зависимость амплитуды волны от времени имеет вид exp −i t . Поэтому если собственное значение′ i " имеет положительную мнимую часть" , волна со временем нарастает, а если отрицательную, то затухает. Мнимую часть " в теории плазмы обозначают также буквой и называют инкрементом (growth rate в англоязычной литературе). Это значит, что такая функция распределения неустойчива (рис. 20б).
Физически это можно объяснить следующим образом. Рассмотрим частицу, которая движется почти с фазовой скоростью волны, но чуть медленнее её. Горб потенциала волны догоняет частицу и ускоряет её. Тем самым, волна теряет часть энергии. Частица отражается от горба и начинает догонять волну. Но для того, чтобы отдать энергию следующему горбу, частица должна двигаться довольно долго, т.к. её скорость почти равна фазовой скорости. За это время она может испытать столкновение и выйти из резонансной
105
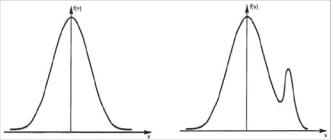
области. Частица, которая опережает волну, отдаёт свою энергию горбу, который она догоняет, отражается от него и также выбывает из резонанса за счёт столкновений. Таким образом, если частиц, отстающих от волны, больше, чем опережающих,
т.е. |
∂f0e |
0, то волна затухает. Если же наоборот, |
|
∂p |
|||
|
|
то раскачивается.
а |
б |
Рис. 20. Равновесные функции распределения. a − устойчивая (волна затухает) и б − неустойчивая (волна раскачивается)
IV.5. Диэлектрическая проницаемость максвелловской плазмы с неподвижными ионами
Диэлектрическая проницаемость связывает напряжённость и индукцию электрического поля,
106

D E
В однородной и изотропной плазме тензор
диэлектрической проницаемости становится диагональным, D E, а соответствующее уравнение Максвелла в фурье-представлении имеет вид:
ik D 0.
Для того, чтобы найти связь между E и D в незамагниченной максвелловской плазме, вернёмся к уравнению (IV.3.5) и перепишем его так:
(IV.5.1)
(IV.5.2)
|
4 e2 |
|
|
∂f0e |
|
|
Ze |
|
|
||
ik 1 |
|
|
dp |
|
|
|
|
|
|
E 0. |
(IV.5.3) |
k |
∂p |
|
− |
|
kp |
i |
|||||
|
− |
|
|
m |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Сравнивая (IV.5.2) и (IV.5.3), можно видеть, что диэлектрическая проницаемость максвелловской плазмы в фурье-представлении можно записать следующим образом:
|
4 e |
2 |
|
|
∂f0e |
|
|
|
Ze |
|
|
1 − |
|
|
|
dp |
|
|
|
|
|
. |
(IV.5.4) |
k |
|
∂p |
|
kp |
− 1−i |
||||||
|
|
− |
|
|
|
m |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим эту функцию в явном виде для того
случая, когда равновесная функция распределения является максвелловской,
107
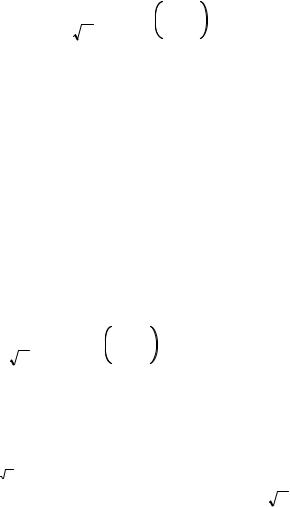
f0 |
|
n |
|
|
p2 |
|
|||||
|
|
|
|
|
exp − |
|
. |
(IV.5.5) |
|||
|
mvT |
pT2 |
|||||||||
Здесь vT2 2T/m; |
pT |
mvT. Решение |
этой |
||||||||
задачи сводится, в сущности, к вычислению |
|||||||||||
интеграла |
|
|
|
|
|
|
|
|
|
|
|
|
∂f0e |
|
Ze |
|
|||||||
K ≡ dp |
|
|
|
|
|
|
. |
(IV.5.6) |
|||
∂p |
|
|
kp |
− 1−i |
|||||||
− |
|
|
|
m |
|
||||||
|
|
|
|
|
|
|
|
|
|
||
. Можно бы прямо воспользоваться формулой (IV.4.3), но мы проведём интегрирование последовательно, фактически выведя эту формулу. Вычислим производную от максвелловской функции и подставим её в (IV.5.6).
|
|
2n |
|
|
|
|
|
|
|
|
p2 |
|
|
p/pT |
dp |
|
||||||||||||||||
K − |
|
|
|
exp |
|
− |
|
|
|
. (IV.5.7) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pT |
||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
kp |
|
i |
|||||||||||||||||
|
|
pT |
|
|
|
|
|
|
pT |
|
|
− m |
|
|
|
|
|
|
|
|||||||||||||
|
|
− |
|
|
|
|
|
mpT |
pT |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Добавим к числителю дроби слагаемое |
|
i |
и |
|||||||||||||||||||||||||||||
|
kpT |
|||||||||||||||||||||||||||||||
вычтем его. Введя новую переменную z p/pT, |
||||||||||||||||||||||||||||||||
перепишем K в следующем виде: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2nm |
|
|
|
|
|
|
|
|
m |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
kpT |
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
K − |
|
|
|
exp −z |
|
|
|
|
|
|
dz |
exp −z |
dz. |
|||||||||||||||||||
|
pT2 k |
|
|
|
z−m |
i |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Последний |
− |
|
|
|
|
|
в |
|
|
kpT |
|
|
− |
равен |
|
|
|
. |
||||||||||||||
|
интеграл |
|
|
|
|
|
(IV.5.8) |
|
|
|
||||||||||||||||||||||
Обозначим х |
|
m |
, 1 |
|
|
|
|
|
и перепишем первый |
|||||||||||||||||||||||
|
|
|
kpT |
|
||||||||||||||||||||||||||||
|
|
|
|
|
kpT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
интеграл в (IV.5.8) в следующем виде:
108
|
|
|
m |
i |
|
|
|
|
m |
i |
|
|
|
|
exp −z2 |
|
kpT |
|
dz |
exp −z2 |
kpT |
dz. (IV.5.9) |
|||||
|
|
|
|||||||||||
z − m |
i |
|
z − x − i 1 |
||||||||||
− |
|
|
kpT |
|
− |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
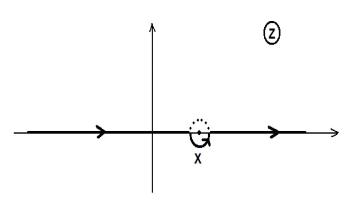
Интегрирование здесь можно выполнить вдоль действительной оси в комплексной плоскости z (рис. 21.
Подынтегральная функция в верхней полуплоскости имеет полюс вблизи действительной оси, около которой линейное приближение неприменимо. Однако можно обойти полюс по полуокружности снизу, так как интеграл от точной поправки к функции распределения не имеет полюсов между действительной осью и выбранной дугой. Дугу выбираем так, что на ней всё еще применима теория возмущений, но экспонента под интегралом мало отличается от её значения на действительной оси под полюсом.
Рис. 21. Контур интегрирования в (IV.5.9)
Тогда интеграл (IV.5.9) распадается на два: интеграл в
109

смысле главного значения при → 0 и интеграл по дуге. Интеграл по дуге равен половине интеграла по окружности вокруг полюса, который по теореме о вычетах равен 2 i exp −x2 . Окончательно получаем:
k, 1 |
4 ne2 |
1 F |
|
|
. |
|||
k2T |
kvT |
|||||||
Здесь |
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
x |
|
exp −z2 |
|
|
|
||
F x |
|
|
z − x |
dz |
|
|||
|
|
− |
|
|
|
VP |
||
|
|
|
|
|
|
|||
|
i |
x exp −x2 . |
|
|||||
(IV.5.10)
(IV.5.11)
Эта функция табулирована. Её также можно
представить в виде ряда при х |
|
|
→ 0 и в виде |
|||||||||||||||||
kvT |
||||||||||||||||||||
асимптотического |
|
|
ряда |
|
при |
→ . |
При |
|||||||||||||
|
|
|
х |
|||||||||||||||||
x 1 |
дробь |
1 |
|
|
|
|
|
|
представляется |
в |
||||||||||
|
z x |
|
|
|
|
|
||||||||||||||
виде: |
1 |
− |
1 |
1 |
|
z |
|
|
z |
3 . . . |
. |
|
Подставляя |
|||||||
z x |
x |
x |
x |
|
||||||||||||||||
это выражение в (IV.5.11) и учитывая, что нечётные |
||||||||||||||||||||
члены при интегрировании выпадут, получаем: |
|
|||||||||||||||||||
|
|
F x − |
1 |
1 |
|
|
|
|
3 |
|
. . . |
|
(IV.5.12) |
|||||||
|
|
2x2 |
4x3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
i x exp −x2 ; x 1.
Вобратном предельном случае x 1 действительную часть Re F x можно преобразовать следующим образом:
110
