
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf
Hr |
∂ |
|
H0 |
m − nq |
∂ |
0. |
(II.3.9) |
|
∂r |
Rq |
∂ |
||||||
|
|
|
|
|
Это уравнение в частных производных первого порядка, которое решается методом характеристик. Характеристика имеет вид:
|
|
|
dr |
|
d |
qR |
|
|
|
|
|
|
|
m − nq |
H0 , |
(II.3.10) |
|
|
|
|
Hr |
|||||
где Нк определяется первым из выражений |
||||||||
(II.3.3), Hr |
m |
A1 cos . |
|
|
||||
r |
можно |
написать в |
||||||
Решение |
этого |
уравнения |
||||||
общем виде в квадратурах, однако для анализа его удобно получить в явном виде вблизи резонансной поверхности. Пусть r0 − радиус невозмущенной резонансной поверхности, для которой m − nq 0. Введём новую переменную r r − r0 и разложим m − nq в ряд вблизи т. r0 :
m − nq ≈ −nq′ r. |
(II.3.11) |
Тогда уравнение (II.3.10) перепишется так:
nq |
′ |
r |
d r |
− |
R |
m |
A1 cos . |
(II.3.12) |
|
d |
H0 |
r0 |
Это уравнение легко интегрируется:
r |
2 |
−2 |
m |
RA1 |
sin C, |
(II.3.13) |
|
n |
SH0 |
71

Здесь С − постоянная. Отсюда получаем:
r |
2 С − |
m |
RA1 |
sin . |
(II.3.14) |
n |
SH0 |
Общим решением уравнения (II.3.9) является функция С . Оно существует в области действительных величин, если существуют действительные значения (II.3.14), т.е. если
|
|
С − |
m RA1 |
|||||||||
|
|
n |
SH0 sin ≥ 0. |
|||||||||
Если С − |
m |
|
|
|
RA1 |
, решений нет ни при каких . |
||||||
|
n |
|
|
|||||||||
|
|
|
SH0 |
|||||||||
Если С − |
m |
|
|
RA1 |
, решение существует лишь в |
|||||||
n |
|
|||||||||||
|
|
|
|
SH0 |
||||||||
отдельных точках |
||||||||||||
− |
|
|
2 k, где k 0, 1, 2. . . |
|||||||||
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|||
При этом |
|
r 0, магнитные поверхности |
||||||||||
представляют собой отдельные спиральные нити,
лежащие |
|
на |
невозмущённой |
поверхности |
|||||
r r0. Рассмотрим сечение |
этих |
поверхностей |
|||||||
const. |
Мы |
видим на |
периоде |
2 m точек |
|||||
|
|
2 k−1 |
. |
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
||
|
Пусть теперь |
|
|
|
|
||||
|
|
|
|
|
m RA1 |
|
С |
|
|
|
|
С − |
n |
SH0 С, |
где |
|
1. |
||
|
|
С |
|||||||
(II.3.15)
(II.3.16)
(II.3.17)
72

Тогда |
|
|
|
|
r |
2 С − |
m RA1 |
sin − 1 , |
(II.3.18) |
n SH0 |
т.е. сечения магнитных поверхностей образуют маленькие овалы вокруг новых магнитных осей
(II.3.16). |
|
|
|
|||
Пусть |
С растет и |
дорастает до |
величины |
|||
С |
m |
|
RA1 |
. Тогда решения есть при всех , но при |
||
n |
|
SH0 |
||||
sin −1 |
оба корня |
r равны |
нулю, т.е. |
|||
соответствующие точки лежат на невозмущенной
поверхности, а соответствующая поверхность отделяет области, где возмущенные поверхности охватывают новые магнитные оси от области, где возмущенные поверхности охватывают основную магнитную ось. Эта поверхность является сепаратрисой, т.к. при С решения
существуют при всех .
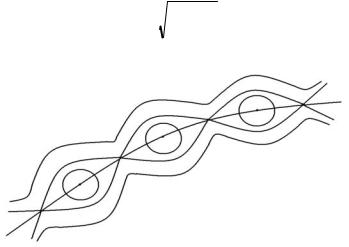
Сечение возмущенных поверхностей показано на рис. 17.
Из рис. 17 видно, что возмущенные поверхности образуют систему магнитных островов вблизи резонансной поверхности. Заметим, что острова образуются при сколь угодно малых A1. Таким образом, магнитные поверхности оказываются неустойчивыми по отношению к резонансному возмущению и меняют свою топологию вблизи резонансной поверхности.
Максимальная ширина острова равна 2 rmax,
73
rmax 2 |
mRA1 . |
(II.3.19) |
|
nSH0 |
|
Рис. 17. Сечение возмущенных магнитных поверхностей
Легко видеть, что с ростом шира S ширина острова уменьшается. При S → 0 ширина острова стремится формально к бесконечности, и для того, чтобы её рассчитать, нужно учитывать следующие члены разложения в (II.3.11).
Мы рассчитали структуру магнитных поверхностей, когда возмущение описывается одной гармоникой. Однако, в реальной ситуации возмущение представляет собой набор гармоник. Это может привести к перекрытию островов. Пусть теперь возмущение представляет собой две гармоники с одинаковыми тороидальными волновыми числами n и соседними полоидальными волновыми числами m и m 1. Резонансными для
74

них будут поверхности, соответствующие q1 |
|
m |
и |
||||||||||
n |
|||||||||||||
q2 |
|
m 1 |
. Пусть q слабо зависит от радиуса, |
т.е. |
|||||||||
n |
|||||||||||||
q2 |
≈ q1 q′ r1 r, где |
r |
− расстояние |
между |
|||||||||
резонансными поверхностями |
|
|
|
|
|
||||||||
|
|
|
|
|
r |
1 |
|
. |
|
|
|
(II.3.20) |
|
|
|
|
|
|
nq′ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Если это расстояние меньше ширины острова, |
||||||||||||
|
1 |
2 |
mRA1 |
, |
|
|
(II.3.21) |
||||||
|
|
|
|
nq′ |
nSH0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
то острова перекрываются, и, согласно критерию Чирикова (см. напр. [8]), силовые линии внутри области перекрытия могут блуждать случайным образом.
Заметим, что в токамаке с сепаратрисой узкая зона вблизи сепаратрисы практически всегда стохастизована. Дело в том, что при q → на конечном отрезке радиуса резонансные поверхности лежат очень часто, а спектр возмущений довольно широк. Возмущения присутствуют всегда. В частности, они вызваны тем, что тороидальное поле создаётся не сплошной намоткой, а отдельными катушками. Подробрее об этом см. в работе [8].
Задача
Определить структуру возмущенных поверхностей вблизи резонансной поверхности для случая, когда профиль q имеет экстремум точно на резонансной поверхности.
75

Решение
Вместо разложения (II.12.11) имеем:
m − nq ≈ −nq′′ r 2 , 2
а вместо (II.3.12) и (II.3.13) −
nq |
′′ d r 2 |
− |
R |
m |
|
A1 cos и |
||||
|
2d |
|
H0 |
r0 |
|
|||||
r |
3 |
−6 |
m RmA1 |
sin C. |
||||||
|
n |
H0q′′ |
||||||||
Отсюда видно, что для r существуют решения при любых , т.е. острова исчезают.
76
Глава III. Траектории частиц в токамаке
Магнитная ловушка для плазмы в первую очередь должна хорошо удерживать отдельные частицы. Тороидальные системы в этом смысле имеют преимущество перед открытыми ловушками, т.к. не имеют конуса потерь. С другой стороны, просто тороидальный соленоид не может удерживать частицы, т. к. они уходят из него вследствие дрейфа. Дрейф в неоднородном тороидальном поле приводит к разделению зарядов
внаправлении верх-низ, а образовавшееся при этом электрическое поле вследствие ЕхВ дрейфа заставляет частицы выдрейфовывать из системы вдоль большого радиуса. Ток, текущий в токамаке, превращает круговые силовые линии тороидального соленоида в спирали, намотанные на тороидальные магнитные поверхности, создавая так называемое вращательное преобразование. В стеллараторе аналогичный эффект создаётся внешними винтовыми обмотками. Такая конфигурация поля превращает траектории частиц
взамкнутые. Рассмотрим эти траектории в токамаке с малой тороидальностью.
Магнитное поле в токамаке можно представить в виде:
77

H H0R0 , |
H0R0 |
|
1 |
e , (III.1) |
|
R |
R0 |
||||
|
|
|
|||
Квазицилиндрическая |
система |
|
координат |
||
показана на рис. 18.
Рис. I8. Квазицилиндрическая система координат. |
|
Как видно из рисунка, |
|
R R0 − r cos . |
(III.2) |
Тороидальное поле, которое в токамаке всегда много больше, чем полоидальное, при a/R 1 можно приближенно представить в виде:
78

|
|
H |
|
H0R0 |
≈ H0 1 |
|
r |
cos |
. |
(III.3) |
|||
|
|
|
|
R |
R0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Как было показано в разделе II, уравнение для |
|
|||||||||||
дрейфовой траектории имеет вид: |
|
|
|
||||||||||
|
dr |
hv |
c |
E, H |
mc |
|
|
v2 |
2v2 |
h, H . |
(III.4) |
||
|
|
|
2eH2 |
||||||||||
|
dt |
H |
|
|
|
|
|
||||||
|
Для простоты положим |
Е 0, хотя наличие |
|
||||||||||
равновесного электрического поля приводит к ряду |
|
||||||||||||
интересных эффектов, в частности, к пинчеванию |
|
||||||||||||
разряда, которое рассмотрим позже. Учтем, что |
|
||||||||||||
сохраняются |
|
кинетическая |
|
|
энергия |
частицы, |
|
||||||
mv2/2 const, |
|
|
и |
её |
магнитный |
момент |
|
||||||
mvH2
const. Заметим, что здесь магнитный
момент отличается от определённого ранее постоянным множителем. Это связано с тем, что теория, изложенная ниже, даётся по работе [9], и мы следуем обозначениям автора. Вычислим H.
|
H |
H2 H2 |
|
(III.5) |
|
|
2 |
r |
2 |
|
|
|
2 |
|
|||
|
H0 1 |
|
cos |
H . |
|
R0 |
|
||||
Сохраняя в |
(III.5) |
только |
линейные |
по |
|
r/R0 члены, получаем:
79
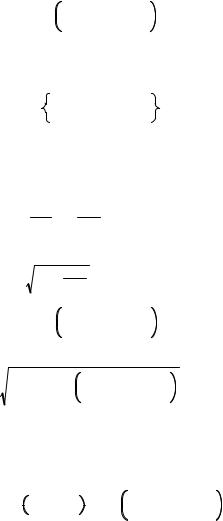
H H0 |
1 |
r |
cos , |
(III.6) |
|
||||
|
|
R0 |
|
|
или в компонентах |
|
|
|
|
H H0 |
cos , sin , 0 . |
(III.7) |
||
|
R0 |
R0 |
|
|
Уравнение для |
-компоненты |
траектории |
||
принимает вид:
r ddt HH v ,
или, если выразить v через и полную скорость v, v v 1 − mvH2 , то
|
|
|
|
d |
|
|
|
v |
1 |
− |
|
r |
|
cos |
|
(III.8) |
||||||||
|
|
|
|
dt |
R0q |
R0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 − |
|
H0 |
|
1 |
|
r |
|
cos . |
|
||||||||||
|
|
|
|
|
mv2 |
R0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Здесь q |
rH0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
R0H . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Радиальная компонента уравнения (III.4) даёт: |
|
|||||||||||||||||||||||
|
dr |
|
|
mc |
|
|
|
v2 v2 |
|
sin |
1 |
r |
cos . |
(III.9) |
||||||||||
|
|
2eH0R0 |
|
|
||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
|||||||||
Отклонение частицы от силовой линии предполагается небольшим, поэтому уравнение
80
