
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf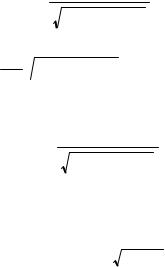
x x0 t |
c2Etdt |
|
(I.2.5) |
0 |
E02 ceEt 2 |
|
|
eE1  E20 ceEt 2 x0.
E20 ceEt 2 x0.
Аналогично получаем зависимость у от времени:
dy |
|
py0c |
2 |
|
|
|
|
py0c2 |
|
|
dt |
|
|
|
|
|
|
|
|
, |
(I.2.6) |
E |
|
|
|
|
|
|||||
|
|
|
|
E |
02 ceEt 2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
py0c |
Arsh |
ceEt . |
|
||
|
|
|
|
eE |
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
Напомним, что Arsh x ln x |
x2 1 . |
|
||||||||
В отличие от нерелятивистского случая при достаточно больших временах х растет со временем практически линейно, а у – логарифмически.
Задача.
Найти предел по времени, когда движение еще будет оставаться нерелятивистским.
Решение.
Движение можно считать нерелятивистским,
если px mc, т.е. E mc/ eE .
Теперь перейдем к рассмотрению движения релятивистской частицы в однородном магнитном поле. Пусть электрическое поле однородно и перпендикулярно магнитному. В этом случае всегда
21
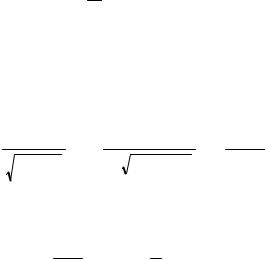
можно выбрать такую систему отсчета, в которой оно равно нулю. Однородное магнитное поле H const может быть описано скалярным потенциалом
A H, R /2. |
(I.2.7) |
Действительно,
rot H, r Hdivr − H, r r, H − r H 3H − H
div r 3, H, r Hz ∂∂z x, y, z H.
Выберем систему координат так, чтобы векторный потенциал имел только одну компоненту Ax H y, Ax Az 0. В этом случае магнитное поле имеет только одну z-компоненту Н.
Импульс частицы можно выразить через ее кинетическую энергию:
|
p |
m |
|
V |
|
mc2V |
|
EkinV |
. |
|||||
|
|
|
1 − |
v2 |
|
|
|
c2 1 − v2/c2 |
|
c2 |
||||
|
|
|
c2 |
|
|
|
|
|||||||
Следовательно, |
уравнение |
|
движения |
|||||||||||
ṗ |
e |
V, H можно представить в виде: |
|
|
||||||||||
c |
|
|
||||||||||||
|
|
|
|
|
Eckin2 |
|
dV |
|
e |
V, H , |
|
(I.2.8) |
||
|
|
|
|
|
dt |
c |
|
|||||||
Раскрывая векторное произведение в правой части
(I.2.8), имеем:
|
ex |
ey |
ez |
|
|
V, H |
Vx |
Vy |
Vz |
|
(I.2.9) |
|
0 |
0 |
Hz |
|
|
|
|
|
|
|
|
22
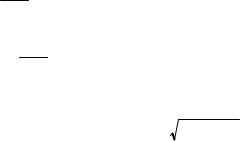
ex Vy H − ey Vx H ez 0
Отсюда сразу получаем Vz 0. Для двух других компонент скорости получаем:
Ekin |
|
|
|
e |
|
|
|
|
|
||
|
Vx |
|
Vy H →Vx |
H Vy; |
(I.2.10) |
||||||
|
c |
||||||||||
c2 |
|
|
|
|
|
|
|
|
|
||
|
Ekin |
|
|
|
|
e |
|
|
|
||
|
|
Vy |
−Vx H |
→ |
− H Vx |
|
|||||
|
c |
|
|||||||||
|
|
c2 |
|
|
|
|
|
|
|||
Здесь мы ввели циклотронную частоту
H |
ecH |
|
ecH |
1 − v2/c2 |
|
Ekin |
|
mc2 |
|
и комплексную скорость V Vx iVy. Тогда уравнение движения (I.2.10) можно переписать в виде одного комплексного уравнения
|
|
|
|
V −i H V |
|
Решение этого уравнения имеет вид
V ae− Ht,
где произвольную константу a можно представить в виде
(I.2.11)
(I.2.12)
(I.2.13)
a V0e−i . |
(I.2.14) |
Выражения (I.2.13) и (I.2.14) можно переписать в компонентах
23

Vx V0 cos Ht ; Vy V0 sin Ht ; |
(I.2.15) |
Vz Vz0.
.
Интегрируя (I.2.15) по времени, получаем уравнения траектории:
x0 sin Ht ,
y y0 |
cos Ht , |
(I.2.16) |
||
z z0 Vz0t. |
|
|||
Здесь |
V0 |
− величина, |
называемая |
|
H |
|
|||
ларморовским радиусом или гирорадиусом.
Легко видеть, что траектория представляет собой спираль радиуса . Заметим, что циклотронная частота в нерелятивистском приближении не зависит от скорости частицы, H eHmc , но при приближении скорости света она заметно уменьшается. Это является причиной того, что в циклотроне нельзя ускорять частицы до релятивистских скоростей. Факт этот наблюдается экспериментально и является одним из прямых экспериментальных подтверждений теории относительности.
Как уже было замечено ранее, траекторию движения частицы в скрещенных (взаимно перпендикулярных) электрическом и магнитном полях можно получить из решения предыдущей задачи, перейдя с помощью преобразования
24

Лоренца в систему отсчета, в которой поля равны заданным величинам. Особенно просто это сделать в нерелятивистском случае, когда магнитное поле остается неизменным, а в движущейся со скоростью V системе появляется поле E′ − 1c V, H .
Получим траекторию частицы в однородных электрическом и магнитном полях для нерелятивистского случая прямым вычислением.
Пусть магнитное поле направлено вдоль оси z, а электрическое поле имеет две компоненты
H0, 0, H , E 0, Ey, Ez . Уравнения движения
внерелятивистском случае имеет вид:
m V eE ec V, H ,
что в компонентах можно переписать как:
|
e |
|
|
|
m x |
c |
y H, |
(I.2.17) |
|
|
|
|
e |
|
m y eEy − |
c |
x H, |
||
m z eEz
Зависимость координаты z от времени получается сразу интегрированием по времени:
|
e |
|
|
|
|
|
|
z |
Ezt Vz0, |
(I2.18) |
|||||
m |
|||||||
|
e |
|
2 |
2 |
|
|
|
z |
|
Ez t |
|
Vz0t z0. |
|
||
2m |
|
|
|||||
Снова введем комплексную скорость, умножим у-компоненту на i и сложим ее с х-компонентой. В результате имеем:
25
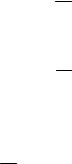
V i H V i me Ey.
Умножаем (I.2.15) на ei Ht.
d |
|
i Ht |
|
e |
|
i Ht |
|
dt |
V e |
|
i |
m |
Eye |
|
. |
Интегрируем (I.2.20) и, разделив на находим комплексную скорость:
(I.2.19)
(I.2.20)
ei Ht,
|
|
|
e |
|
Ey |
|
|
|
|
|
|
|
V ae |
−i Ht |
|
|
e |
i Ht |
− 1 e |
−i Ht |
(I.2.21) |
||||
|
m |
|
H |
|
|
|||||||
и ее компоненты: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Ey |
|
|
|
x V0 cos Ht c |
|
, |
|
(I.2.22) |
||||||||
H |
|
|||||||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
y −V0 sin Ht |
|
|
|
|
|
|||||||
Таким образом, частица ускоряется равномерно в направлении магнитного поля и вращается в направлении, перпендикулярном последнему. На это вращение наложено равномерное смещение в направлении, перпендикулярном как электрическому, так и магнитному полям со скоростью
|
|
|
VD |
c |
E, h , |
h |
H |
. |
(I.2.23) |
|
|
|
H |
|
|||||
|
|
|
|
|
|
H |
|
||
|
Условие применимости этой формулы VD c, |
|
|||||||
т.е. |
|
Ey |
1. |
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
||
Эту скорость называют дрейфовой. Заметим, что направление дрейфа не зависит от заряда частицы. Таким образом, электроны и ионы
26

дрейфуют в одном направлении.
Задача.
МГД-генератор – это устройство для непосредственного преобразования тепловой энергии в электрическую. Струю плазмы вдувают в направлении, перпендикулярном магнитному полю, в пространство между полюсами магнита. Магнитное поле отклоняет электроны в одну сторону, а ионы – в другую. Заряженные частицы собираются на двух электродаx, на одном – электроны, на другом – ионы. Таким образом, между электродами создается разность потенциалов.
Определить эту разность потенциалов, если скорость плазмы V0, расстояние между электродами d, а напряженность магнитного поля
– Н. Электростатической экранировкой пренебречь.
Решение.
Разность потенциалов на электродах будет расти до тех пор, пока сила, действующая на частицы плазмы со стороны электрического поля, создаваемого зарядами на электродах, не уравновесит силу Лоренца, т.е.
eE 1c VH.
Разность потенциалов U Ed. В результате получаем:
27

U ecd VH.
I.3. Движение частиц в аксиально симметричном магнитном поле. Задача Штермера
Еще в первой половине ХХ века геофизики обнаружили, что вблизи поверхности Земли существует поток быстрых заряженных частиц, который зависит от географических координат точки наблюдения. Одной из первых попыток объяснения величины этих потоков являлась теория Штермера, рассмотревшего движение потока заряженных частиц в магнитном поле Земли, которое он аппроксимировал магнитным полем диполя. И хотя реальное магнитное поле Земли на больших расстояниях не имеет ничего общего с дипольным (см. рис. 4), на расстояниях порядка нескольких земных радиусов такая аппроксимация дает хорошие результаты (см. напр. [2]). Конечно, уточнение экспериментальных данных, а также последующие спутниковые измерения привели к существенному развитию теории, но теория Штермера представляет интерес и в настоящее время. Неожиданное применение теория Штермера и ее модификации нашли во второй половине ХХ века, когда впервые начали проектировать полет обитаемого корабля на Марс. Дело в том, что потоки заряженных частиц, выбрасываемые
28

Солнцем при вспышках, представляют серьезную опасность для космонавтов. Одним из способов защиты космического аппарата от таких потоков является создание магнитных полей, отклоняющих частицы от обитаемого отсека [3].
Рис. 4. Магнитное поле Земли. Расстояния указаны в радиусах Земли
Точное решение уравнений движения частицы в поле диполя возможно лишь численно. Однако интегралов движения в осесимметричном поле оказывается достаточно для нахождение потоков частиц, приходящих из бесконечности в точку наблюдения. Естественно, что торможение частиц в атмосфере Земли не учитывается.
Как было выяснено в разделе I.1, при движении заряженной частицы в произвольном аксиально
29
симметричном магнитном поле существуют два интеграла движения: кинетическая энергия (и, как следствие, полная скорость) и полоидальная компонента обобщенного импульса (I.1.10). Исторически принято обозначение P ≡ 2 .
С помощью (I.1.10) можно выразить полоидальную скорость через интегралы движения и координаты точки наблюдения r и :
̇ |
|
2 |
− |
e |
A |
|
1 − |
V2 |
(I.3.1) |
|
mr sin |
c2 |
|||||||||
r sin ≡ V |
|
cm |
|
Очевидно, что вычисленная таким образом полоидальная скорость не может превосходить полную скорость, т.е.
|
Q ≡ |
v |
|
|
|
(I.3.2) |
||
|
v |
|
|
|||||
|
2 |
− |
|
e |
|
A 1 − |
v2 |
≤ 1 |
mr sin |
|
cH |
|
c2 |
||||
|
|
|
|
|
|
|||
Таким образом, если заданы начальные интегралы движения, равенство в нестрогом неравенстве (I.3.2) задает поверхность в обычном пространстве, разделяющую области, в которых могут двигаться частицы с заданными начальными условиями, от тех, в которые они попасть не могут. Получим такие поверхности для магнитного диполя. Для этого введем безразмерные величины
 |
4 S2 |
A ; |
̂ |
|
|
; |
(I.3.3) |
|
|
pS |
|||||||
− 2 |
30
