Морозов Введение в теорию горячей плазмы Част2 2013

Министерство образования и науки Российской Федерации

Национальный исследовательский ядерный университет «МИФИ»

Д.Х. Морозов

Введение в теорию горячей плазмы

Часть 2

Рекомендовано к изданию УМО «Ядерные физика и технологии»

Москва 2013

УДК 533.9.01(075.8)+621.039.616/.66(075.8) ББК 22.333я7+31.292я7 М80

Морозов Д.Х. Введение в теорию горячей плазмы. Ч. 2. М.:

НИЯУ МИФИ, 2013. – 100 с.

Во второй части пособия «Введение в теорию горячей плазмы» на основе теоретических представлений, изложенных в первой части, рассматриваются основные элементы теории равновесия и устойчивости горячей плазмы в тороидальных системах. Излагается неоклассическая теория переноса в токамаке. Пожалуй, впервые в учебной литературе представлены элементы теории плазмы с примесями, играющие очень важную роль для холодных периферийных областей термоядерных устройств. Несмотря на сравнительно небольшой объём, занимаемый холодной периферийной плазмой, периферия в ряде случаев играет определяющую роль в проблеме удержания. В частности, именно процессы в периферийной области вызывают срыв разряда во всем объёме (так называемый большой срыв).

Как и первая часть пособия, вторая часть предназначена для студентов старших курсов и аспирантов физических факультетов вузов.

Подготовлено в рамках Программы создания и развития НИЯУ МИФИ.

Рецензенты: д-р физ.-мат. наук, проф. В.И. Ильгисонис, д-р физ.-мат. наук, проф. В.М. Жданов

ISBN 978-5-7262-1809-0

© Национальный исследовательский ядерный университет

«МИФИ», 2013

2

3

ПРЕДИСЛОВИЕ

Настоящее учебное пособие основано на курсе лекций, который в течение ряда лет читается студентам кафедры физики плазмы НИЯУ МИФИ. В пособии изложены основные явления в горячей плазме и теоретические методы их изучения. Рассмотрены траектории отдельных частиц в электрических и магнитных полях, структура магнитных полей в токамаке, кинетическое и магнитогидродинамическое описание плазмы как сплошной среды, рассмотрены линейные колебания и волны в однородной плазме, бесстолкновительное затухание Ландау, а также ряд нелинейных явлений.

Вторая часть пособия в большей степени ориентирована на теорию магнитного удержания.

Основная часть второй части пособия посвящена трём наиболее важным проблемам в теории магнитного удержания:

1.Равновесие в системах с замкнутыми магнитными поверхностями.

2.Устойчивость плазмы в системах для магнитного удержания.

3.Перенос тепла и частиц.

Раздел первый (глава 1) посвящен равновесию плазмы в тороидальных системах. Получено уравнение Шафранова–Грэда и рассмотрено равновесие плазмы в токамаке.

Второй раздел изложен в главах 2–4.

В главе 2 рассмотрены два подхода: энергетический принцип и метод малых возмущений.

Глава 3 посвящена следующим неустойчивостям идеальной плазмы:

1.Винтовая и желобковая неустойчивости.

2.Температурно-дрейфовые неустойчивости на ионах (ITG мо-

да).

3.Неустойчивость на запертых частицах.

Две важные диссипативные неустойчивости рассматриваются в главе 4. Это тиринг-мода и дрейфовая диссипативная неустойчивость.

Глава 5 содержит элементы теории переноса. Рассмотрены классическая и неоклассическая теории и приведён ряд результатов, посвященных аномальному переносу. К сожалению, за пределами

4

данного пособия остались результаты нелинейного переноса на баллонных модах.

Глава 6 посвящена плазме с примесями. Анализируются различные виды излучения из плазмы и приведены аппроксимационные формулы для скоростей ионизации, рекомбинации и интенсивностей излучения. Рассмотрены радиационно-рекомбинационная неустойчивость и такое интересное явление, как MARFE (Microfaceted Asimmetric Radiation From the Edge).

ГЛАВА 1. РАВНОВЕСИЕ ПЛАЗМЫ В СИСТЕМАХ

СЗАМКНУТЫМИ МАГНИТНЫМИ ПОВЕРХНОСТЯМИ

1.1.Уравнение Шафранова–Грэда

Рассмотрим равновесное стационарное состояние плазмы в системе с замкнутыми магнитными поверхностями. Оно описывается уравнениями двухжидкостной гидродинамики для электронов и ионов соответственно:

mi ni (Vi , )Vi =- Pi + Zeni [Vi ,H]+Fi ;

Здесь F – сила трения между электронами и ионами. Если скорость макроскопического движения плазмы V мала по сравнению с тепловой скоростью VT, то инерционными членами в левых частях (1.1.1) можно пренебречь. Действительно, градиент давления в правых частях можно представить как nmVT2/2a, где a – характерный масштаб профиля давления. Если масштаб изменения профиля скорости имеет тот же порядок, что и профиль давления, то инерционный член в левых частях (1.1.1) мал по сравнению с градиентом давления. В противном случае инерционный член следует‒ учитывать. Сложив два уравнения, c учётом ji = Ze Vi, je= enVe, j=je+ji, P=Pe+Pi, получаем условие равновесия при дозвуковых скоростях вращения плазмы:

Заметим, что мы пренебрегли вязкостью плазмы.

5

В случае околозвуковых или сверхзвуковых течений член mi ni(Vi. )Vi также следует сохранять.

К уравнению (1.1.2) следует добавить стационарные уравнения

Таким образом, давление постоянно вдоль силовых линий. Умножая то же уравнение на j скалярно, находим, что давление

постоянно вдоль линий тока

В замагниченной плазме можно ввести магнитное давление H 2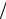(8π). Тогда, используя уравнение (1.1.3) и равенство

[rotH,H]= − H 2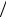2+(H, )H ,

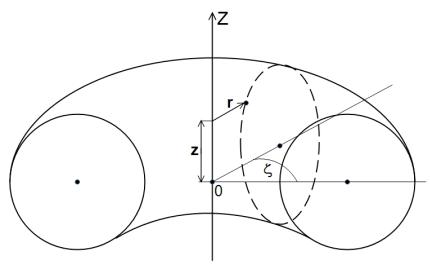
условие равновесия (1.1.2) можно переписать через полное давление Ptot = P+ H2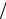(8π)

В качестве примера рассмотрим простейшую цилиндрически симметричную плазменную конфигурацию, ось которой совпадает с осью z. Пусть ток в такой конфигурации течёт вдоль этой оси. Магнитное поле имеет две составляющие, осевую Hz(r), направленную вдоль оси z, и азимутальную Hθ = Hθ (r,z) . Тогда r и

Уравнение (1.1.8) означает лишь однородность конфигурации вдоль оси z. Уравнение (1.1.7) должно быть дополнено уравнения-

6

ми Максвелла. Полученные уравнения выражают давление через магнитное поле, но не могут служить для определения того и другого по отдельности. Эту задачу можно решить только с использованием уравнений переноса.

Для рассмотрения реальных плазменных конфигураций, например, токамака, используется так называемое уравнение Шафрано- ва–Грэда. Оно было получено сначала В.Д. Шафрановым, а затем, независимо от него, Грэдом. Тороидально симметричная конфигурация описывается с помощью системы координат, в которой координатными являются поверхности, параллельные магнитному полю и перпендикулярные ему. В простейшем случае, описанном

Рис. 1. Тороидальная плазменная конфигурация

Магнитное поле в такой системе может быть описано с помощью двух компонент векторного потенциала Aζ (r,z) и Az (r, z).

7

Компоненты магнитного поля выражаются через них следующим образом:

Здесь мы для удобства правые части разделили и умножили на r.

Введем функцию ψ = rAζ . Тогда равенства (1.1.9) перепишутся

В силу цилиндрической симметрии давление плазмы не зависит от угла ζ. Поэтому условие (1.1.5) можно записать в виде

∂∂Pz = ddPψ ∂ψ∂z , видим, что это условие выполняется, если давление

P зависит только от ψ .

Используя (1.1.10), легко видеть, что (H, ψ) = 0. Это означает, что силовые линии магнитного поля лежат на поверхностях

ψ= const .

Встационарном случае сумма уравнений непрерывности для электронов и ионов дает

Таким образом, для тока можно проделать те же операции, что и

Из условия (j, P ) = 0 получаем, что давление плазмы является функцией I.

Тороидальная составляющая магнитного поля легко выражается через функцию I. Действительно, радиальная и осевая составляющие уравнения

8

причём без ограничения общности константу можно положить равной нулю.

Рассмотрим теперь z-ю составляющую уравнения (1.1.14).

Выражая магнитные поля через ψ , это уравнение можно приве-

Воспользуемся радиальной составляющей уравнения равновесия (1.1.2) и подставим в неё Hz из (1.1.10) и jz из (1.13). Кроме

того, учтём, что давление Р зависит только от ψ . В результате, сократив левую и правую части уравнения на ∂ψ / ∂r , получаем следующее выражение для азимутальной составляющей тока:

Окончательно, подставив теперь это выражение в (1.1.18), получим уравнение Шафранова–Грэда

Если задать давление и ток как функции магнитных поверхностей, то есть P = P(ψ) , I = I (ψ) (напомним, что ток выражается

9

через производные от функции I), можно найти форму этих поверхностей. Если задать форму магнитных поверхностей

ψ= ψ(r,z), можно найти связь между током и давлением.

Вкачестве примера рассмотрим тороидально симметричную конфигурацию «сферомак». Его можно представить себе как кольцо с током радиуса R, помещенное во внешнее однородное магнитное поле. Ось симметрии кольца по направлению совпадает с направлением этого поля (рис. 2).

Втакой конфигурации полоидальная составляющая тока равна

нулю, то есть можно положить I = 0. Профиль давления зададим как

если константы A и C связаны соотношением 2A(4+ C) = 4πb.

Переопределив константы, выражение (1.1.23) можно переписать в виде

Рассмотрим форму магнитных поверхностей при различных значениях ψ' :

а) ψ'< 0. В этом случае для r '2 имеется одно положительное решение при всех z′ . Геометрическим местом точек, соответству-

10